编码
- 字母表、字
- 字母表
 是一个有限集,它生成的自由半群为
是一个有限集,它生成的自由半群为![Rendered by QuickLaTeX.com \[ S(A) = \bigcup_{n \geq 1} A^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-23593853e69298dd84a0efe4776caf3f_l3.png)
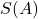 中的元素称为字。字的长度为
中的元素称为字。字的长度为![Rendered by QuickLaTeX.com \[ l: S(A) \to \mathbb{Z}_+,\; l(w) = n, \text{ where } w \in A^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1217a3077384c4d4e5e57a041cff6621_l3.png)
- 字母表
- 基本码字、码字
- 设
 、
、 为字母表。如果
为字母表。如果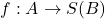 是单射,那么
是单射,那么 称为编码,
称为编码,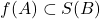 中的元素称为基本码字
中的元素称为基本码字 - 进一步,如果
 的自由扩张
的自由扩张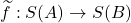 也是单射,那么
也是单射,那么 称为唯一译码的编码,
称为唯一译码的编码,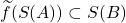 中的元素称为码字
中的元素称为码字
- 设
唯一译码的编码
- 如果
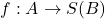 为唯一译码的编码,那么
为唯一译码的编码,那么![Rendered by QuickLaTeX.com \[ \sum_{w \in A} b^{-l(f(w))} \leq 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-916b601ba736be2d6e9daeba6075f0f0_l3.png)
- 设长度为
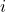 的基本码字的个数为
的基本码字的个数为
长度为![Rendered by QuickLaTeX.com \[ a_i = card\{ w \in A : l(f(w)) = i \},\; i \geq 1, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4b664abf74623f569683eab43b662faa_l3.png)
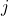 的码字的个数为
的码字的个数为![Rendered by QuickLaTeX.com \[ b_j = card\{ w \in S(A) : l(\widetilde{f}(w)) = j \},\; j \geq 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f00e7c1b34ef5643463dbcd09c7fed00_l3.png)
- 一个长度为
 的码字乘以一个长度为
的码字乘以一个长度为 的基本码字(
的基本码字(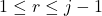 ),或者一个长度为
),或者一个长度为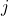 的基本码字是一个长度为
的基本码字是一个长度为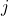 的码字。也就是说,
的码字。也就是说,
进一步,因为![Rendered by QuickLaTeX.com \[ b_{j - 1}a_1 + \cdots + b_1a_{j - 1} + a_j \leq b_j. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ce44e6e11f20c16362e079e4f8c1b982_l3.png)
 为唯一译码的编码,所以相反方向的不等式、以及等式也成立。定义
为唯一译码的编码,所以相反方向的不等式、以及等式也成立。定义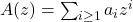 ,
, 。那么,
。那么,![Rendered by QuickLaTeX.com \[ B(z) = B(z)A(z) + A(z). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0f09fe970e31b8029ca73c7ac4a41f2a_l3.png)
- 由于
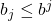 ,故
,故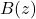 在
在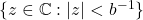 上为解析函数。另一方面,
上为解析函数。另一方面,
所以![Rendered by QuickLaTeX.com \[ B(z) = \frac{A(z)}{1 - A(z)}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-962042ae90c3d3d3b70eb8633cffe040_l3.png)
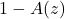 在
在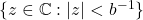 上没有零点。由
上没有零点。由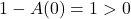 ,可得
,可得
从而,![Rendered by QuickLaTeX.com \[ 1 - A(t) > 0,\; 0 \leq t < b^{-1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-83f40769cd5007435a6b5c070a9c2906_l3.png)
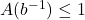 ,并且
,并且![Rendered by QuickLaTeX.com \[ \sum_{w \in A} b^{-l(f(w))} = \sum_{i \geq 1} a_ib^{-i} = A(b^{-1}) \leq 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9f23ebcd76faf0f28cfdb781508fbdf5_l3.png)
- 设长度为
- 反过来,如果
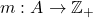 满足
满足
那么存在唯一译码的编码![Rendered by QuickLaTeX.com \[ \sum_{w \in A} b^{-m(w)} \leq 1, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-af390477d0525c71a879281c9f08ef0c_l3.png)
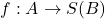 ,使得
,使得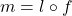
- 定义
我们只需构造一个唯一译码的编码![Rendered by QuickLaTeX.com \[ A_i = \{ w \in A : m(w) = i \},\; a_i = card(A_i),\; i \geq 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7f80564efb4fd8889620d1f81b616aa6_l3.png)
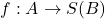 ,使得
,使得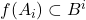 ,
, 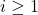
- 由
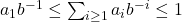 ,可得
,可得
因此,我们可以取![Rendered by QuickLaTeX.com \[ a_1 \leq b. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ed910c5fa0345fde7e62bdaaf1bf2d9b_l3.png)
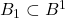 ,使得
,使得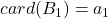 。让
。让 将
将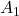 一一映射到
一一映射到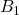
- 由
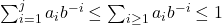 ,可得
,可得
如果![Rendered by QuickLaTeX.com \[ a_j \leq b^j - \sum_{i = 1}^{j - 1} a_ib^{j - i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-688a897d9835877cc58976c22a83dde1_l3.png)
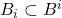 ,
,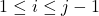 已经取定,并且满足
已经取定,并且满足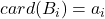 ,那么,由于
,那么,由于
故我们可以取![Rendered by QuickLaTeX.com \[ card[B^j - \cup_{i = 1}^{j - 1} (B_i \times B^{j - i})] \geq b^j - \sum_{i = 1}^{j - 1} a_ib^{j - i} \geq a_j, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-00207989add331da4904fdff47f6d67d_l3.png)
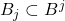 ,使得
,使得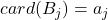 ,并且
,并且
让![Rendered by QuickLaTeX.com \[ B_j \subset B^j - \cup_{i = 1}^{j - 1} (B_i \times B^{j - i}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f1f7ebbc4f6402ebad3153c0c5c54058_l3.png)
 将
将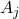 一一映射到
一一映射到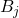
- 由数学归纳法,我们可以得到编码
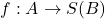 ,满足
,满足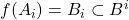 ,
,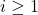 ,并且
,并且
进一步,![Rendered by QuickLaTeX.com \[ B_j \subset B^j - \cup_{i = 1}^{j - 1} (B_i \times B^{j - i}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f1f7ebbc4f6402ebad3153c0c5c54058_l3.png)
 是唯一译码的编码,原因是如果一个码字有两种不同的译码方法,那么我们可以将其从左到右分解为基本码字,直到得到矛盾
是唯一译码的编码,原因是如果一个码字有两种不同的译码方法,那么我们可以将其从左到右分解为基本码字,直到得到矛盾![Rendered by QuickLaTeX.com \[ B_j \cap (B_i \times B^{j - i}) \neq \emptyset \text{ for some } i < j. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-918b10a56a67f3354f294f459dcf54ea_l3.png)
- 定义
最小平均长度
- 设
 为字母表(带有离散
为字母表(带有离散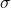 -代数)。如果
-代数)。如果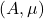 是一个概率空间,那么
是一个概率空间,那么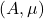 称为基本信源(Elementary Information Source,EIS)
称为基本信源(Elementary Information Source,EIS) - 如果
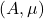 是一个EIS,那么唯一译码的编码
是一个EIS,那么唯一译码的编码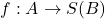 的平均长度为
的平均长度为![Rendered by QuickLaTeX.com \[ \overline{l}(\mu, f) = \sum_{w \in A} l(f(w)) \cdot \mu(w). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ab1b94963c5781f9a62c6751ad18c808_l3.png)
- 进一步,最小平均长度为平均长度的理论极限,
![Rendered by QuickLaTeX.com \[ L(\mu) = \inf\{ \overline{l}(\mu, f) : f: A \to S(B) \text{ is a uniquely decipherable code} \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5c080e05f85c3b126260148906a86430_l3.png)
- 下面我们证明,Shannon熵给出了最小平均长度的最佳估计。设
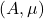 为EIS,并且
为EIS,并且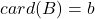 。我们有
。我们有
当![Rendered by QuickLaTeX.com \[ -\sum_{w \in A} \mu(w)\log_b\mu(w) \leq L(\mu) < -\sum_{w \in A} \mu(w)\log_b\mu(w) + 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8cd6304221e85a7231ecbce99094fd66_l3.png)
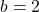 时,
时,
其中,![Rendered by QuickLaTeX.com \[ H(\mu) \leq L(\mu) < H(\mu) + 1, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5e40af7c9ce3f17fa03afc9508d07246_l3.png)
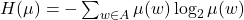 称为Shannon熵
称为Shannon熵
- 由上面的笔记,
![Rendered by QuickLaTeX.com \[ L(\mu) = \inf\bigg\{ \sum_{w \in A} m(w) \cdot \mu(w) : m: A \to \mathbb{Z}_+,\; \sum_{w \in A} b^{-m(w)} \leq 1 \bigg\}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-abd6ef038bc8fb0287fb33f5ff5e8b0f_l3.png)
- 证明左侧不等式:
- 对任意
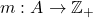 满足
满足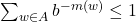 ,定义
,定义![Rendered by QuickLaTeX.com \[ \nu(w) = \frac{b^{-m(w)}}{\sum_{w \in A} b^{-m(w)}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-acb3c2dec9afeb1186856f6665acff64_l3.png)
- 由
可得![Rendered by QuickLaTeX.com \[ m(w) = -\log_b\bigg(\sum_{w \in A} b^{-m(w)}\bigg) - \log_b\nu(w) \geq -\log_b\nu(w), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ba10fd49e1f5f742aa1dd22cca7952e7_l3.png)
其中,最后一个不等式可由Jensen不等式应用于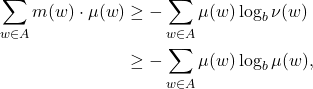
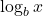 得到,
得到,![Rendered by QuickLaTeX.com \[ -\sum_{w \in A} \mu(w)\log_b\bigg(\frac{\nu(w)}{\mu(w)}\bigg) \geq -\log_b\bigg(\sum_{w \in A} \mu(w)\frac{\nu(w)}{\mu(w)}\bigg) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0b2b1e50b74f1af6b97d120fd7d0a9fd_l3.png)
- 对所有的
 取下确界,左侧不等式成立
取下确界,左侧不等式成立
- 对任意
- 证明右侧不等式:
- 取
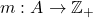 满足
满足![Rendered by QuickLaTeX.com \[ m(w) - 1 < -\log_b\mu(w) \leq m(w),\; w \in A. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5ab50dcc19d57c1b7e071c14b79c6f94_l3.png)
- 那么,
并且![Rendered by QuickLaTeX.com \[ \sum_{w \in A} b^{-m(w)} \leq \sum_{w \in A} \mu(w) = 1, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-732246173edaa815598a3ee098972e2d_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} L(\mu) &\leq \sum_{w \in A} m(w) \cdot \mu(w) \\ &< \sum_{w \in A} \mu(x)[1 - \log_b\mu(x)] \\ &= -\sum_{w \in A} \mu(x)\log_b\mu(x) + 1. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bc6877ffa28179b9e64673237ced63ff_l3.png)
- 取
- 由上面的笔记,