从Euler-Lagrange方程到Hamilton方程
- 我们使用从切空间到局部中的Einstein求和约定
- 在局部坐标系下,Euler-Lagrange方程为
将![Rendered by QuickLaTeX.com \[ \frac{d}{dt}\frac{\partial\mathcal{L}}{\partial\dot{q}^a} - \frac{\partial\mathcal{L}}{\partial q^a} = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1dce7092a0e95477fc585a772c684f85_l3.png)
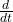 进一步作用于
进一步作用于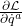 ,可得
,可得
如果![Rendered by QuickLaTeX.com \[ \frac{\partial^2\mathcal{L}}{\partial\dot{q}^a\partial\dot{q}^b}\ddot{q}^b + \frac{\partial^2\mathcal{L}}{\partial\dot{q}^a\partial q^b}\dot{q}^b + \frac{\partial^2\mathcal{L}}{\partial\dot{q}^a\partial t} - \frac{\partial\mathcal{L}}{\partial q^a} = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bb59cd32e4f458fa6fb0b0571b1c9b1b_l3.png)
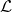 关于
关于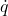 的Hesse矩阵是可逆的,那么上面的方程是广义坐标
的Hesse矩阵是可逆的,那么上面的方程是广义坐标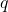 的二阶ODE,正如Newton方程是位置向量
的二阶ODE,正如Newton方程是位置向量 的二阶ODE
的二阶ODE - 我们也可以将Euler-Lagrange方程转化为一阶ODE。令
那么Euler-Lagrange方程变为![Rendered by QuickLaTeX.com \[ p = (p_1, \ldots, p_n) = \bigg(\frac{\partial\mathcal{L}}{\partial \dot{q}^1}, \ldots, \frac{\partial\mathcal{L}}{\partial \dot{q}^n}\bigg), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b049c63b2a5fcf355dc7b169e215cf9e_l3.png)
![Rendered by QuickLaTeX.com \[ \dot{p_a} = \frac{\partial\mathcal{L}}{\partial q^a}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-381525c454872c3072c515f0bd233437_l3.png)
- 定义映射
Jacobi矩阵为![Rendered by QuickLaTeX.com \[ \phi: (q, \dot{q}) \mapsto (q, p), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d2b9816705623bc5b24ae83ce3d3a903_l3.png)
如果![Rendered by QuickLaTeX.com \[ D\phi = \begin{bmatrix}I_n & 0 \\ B & A\end{bmatrix},\; A = \bigg(\frac{\partial^2\mathcal{L}}{\partial\dot{q}^a\partial\dot{q}^b}\bigg),\; B = \bigg(\frac{\partial^2\mathcal{L}}{\partial\dot{q}^a\partial q^b}\bigg). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-47aaa071410e72f3cbdbd28fb9d704e9_l3.png)
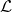 关于
关于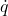 的Hesse矩阵是可逆的,那么
的Hesse矩阵是可逆的,那么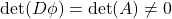 。由从切空间到局部中的逆映射定理,
。由从切空间到局部中的逆映射定理,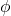 在局部是可逆的,从而是一个坐标变换
在局部是可逆的,从而是一个坐标变换 - 令
 。那么,
。那么,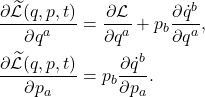
- 如果我们定义Hamiltonian为
那么我们可以得到Hamilton方程![Rendered by QuickLaTeX.com \[ \mathcal{H}(q, p, t) = p_b\dot{q}^b - \widetilde{\mathcal{L}}(q, p, t), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b2144133c80a32f6950f7cfb1d5225fe_l3.png)
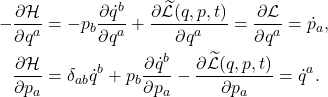
保守力场的Hamiltonian
- 在保守力场中,广义坐标
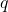 为位置向量
为位置向量 ,广义速度
,广义速度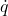 为速度
为速度 ,并且Lagrangian为
,并且Lagrangian为
由此可知,![Rendered by QuickLaTeX.com \[ \mathcal{L} = \frac 12mv^2 - V(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-655a9a2157c4bf5377f70d97cb15fbae_l3.png)
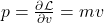 为动量,并且Hamiltonian为总能量,
为动量,并且Hamiltonian为总能量,![Rendered by QuickLaTeX.com \[ \mathcal{H} = p \cdot v - \mathcal{L} = \frac 12mv^2 + V(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-32a0910ce11c193e06ab85b345b730b6_l3.png)
- 坐标变换为
我们称![Rendered by QuickLaTeX.com \[ \phi: (r, v) \mapsto (r, mv),\; \phi^{-1}: (r, p) \mapsto (r, p / m). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8f334d434c381ef474228a33e7be4857_l3.png)
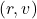 位于坐标空间,
位于坐标空间,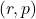 位于相空间。在相空间中,Lagrangian、Hamiltonian分别为
位于相空间。在相空间中,Lagrangian、Hamiltonian分别为![Rendered by QuickLaTeX.com \[ \mathcal{L} = \frac{|p|^2}{2m} - V(r),\; \mathcal{H} = \frac{|p|^2}{2m} + V(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9db195522c537f19a968daa5e27f7b29_l3.png)