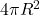参考资料:数学分析
Beta函数
- Beta函数为
![Rendered by QuickLaTeX.com \[ B(p, q) = \int_0^1 x^{p - 1}(1 - x)^{q - 1}dx,\; p, q > 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4bd985ec58cdef6abfb892ce33e243a4_l3.png)
- 我们有
- 对称性
![Rendered by QuickLaTeX.com \[ B(p, q) = \int_1^0 (1 - y)^{p - 1}y^{q - 1}(-dy) = B(q, p). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f1fe1ddd29e78ffe27b18fc8dea7f05a_l3.png)
- 三角函数的任意幂次的积分
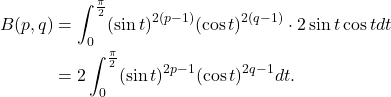
- 对称性
Gamma函数
- Gamma函数为
![Rendered by QuickLaTeX.com \[ \Gamma(s) = \int_0^{+\infty} x^{s - 1}e^{-x}dx,\; s > 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-36256b0da87086e62bb37e2ce3424a30_l3.png)
- 我们有
- 递推公式
由于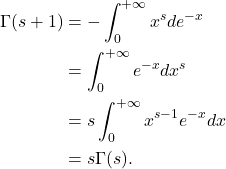
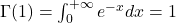 ,故
,故
也就是说,Gamma函数是阶乘函数的推广![Rendered by QuickLaTeX.com \[ \Gamma(n) = (n - 1)!,\; n = 1, 2, \ldots \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bdbac5a60524d8744f4c26d8d6d854b3_l3.png)
- Gauss函数乘以任意幂函数的积分
因此,![Rendered by QuickLaTeX.com \[ \Gamma(s) = \int_0^{+\infty} t^{2(s - 1)}e^{-t^2} \cdot 2tdt = 2\int_0^{+\infty} t^{2s - 1}e^{-t^2}dt. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7d0f664433602dc36dc50997c4b229e2_l3.png)
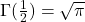
- 递推公式
- Beta函数可以表示为Gamma函数
也就是说,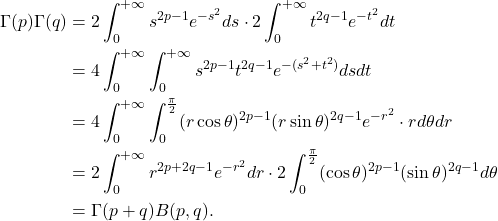
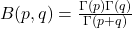
n维球的体积
- 球坐标
其中,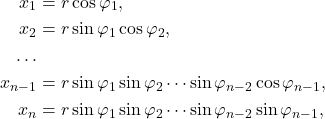
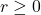 ,
,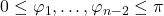 ,
,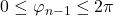
- Jacobi矩阵
- Jacobi矩阵的形式为
其中,第一行的非零元素为![Rendered by QuickLaTeX.com \[ J_n = \begin{bmatrix}* & * & 0 & 0 & \ldots & 0 & 0 \\ * & * & * & 0 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & & \vdots & \vdots \\ * & * & * & * & \ldots & * & 0 \\ * & * & * & * & \ldots & * & * \\ * & * & * & * & \ldots & * & *\end{bmatrix}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c3ffa3e23da9f06e7caab201f28d919a_l3.png)
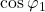 、
、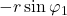
- 对于
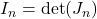 ,如果我们按第一行展开,并且提取出代数余子式中的
,如果我们按第一行展开,并且提取出代数余子式中的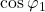 、
、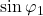 ,那么我们可以得到递推公式
,那么我们可以得到递推公式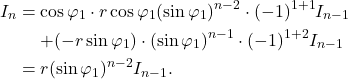
- 最终,
这里,我们使用了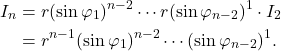
![Rendered by QuickLaTeX.com \[ I_2 = \det\begin{bmatrix}\cos\varphi_{n - 2} & -r\sin\varphi_{n - 1} \\ \sin\varphi_{n - 2} & r\cos\varphi_{n - 1}\end{bmatrix} = r. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-01308b5e19502bc3297792d6c9a197c5_l3.png)
- Jacobi矩阵的形式为
- 半径为
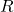 的
的 维球的体积为
维球的体积为
这里,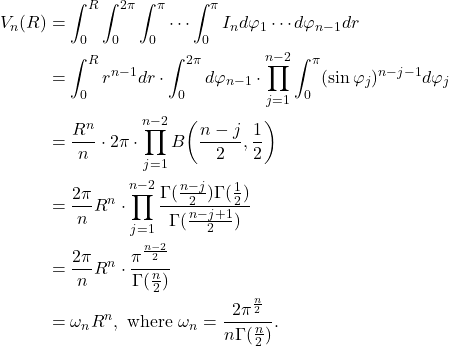
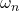 为
为 维单位球的体积
维单位球的体积 - 当
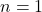 、
、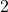 、
、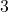 时,我们有
时,我们有
也就是说,区间![Rendered by QuickLaTeX.com \[ \omega_1 = \frac{2\pi^{\frac 12}}{\Gamma(\frac 12)} = 2,\; \omega_2 = \frac{\pi}{\Gamma(1)} = \pi,\; \omega_3 = \frac{2\pi^{\frac 32}}{3\Gamma(\frac 32)} = \frac 43\pi. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-23d0d4bec522c007e885e22c9bc02334_l3.png)
![Rendered by QuickLaTeX.com [-R, R]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-563e20c1689d7f0e7ff1b687c6c5c677_l3.png) 的长度为
的长度为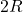 ,半径为
,半径为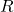 的圆盘的面积为
的圆盘的面积为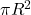 ,半径为
,半径为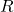 的球体的体积为
的球体的体积为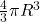
- 我们也可以计算半径为
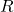 的
的 维球面的面积
维球面的面积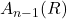 。由
。由
可得![Rendered by QuickLaTeX.com \[ dV_n(R) = A_{n - 1}(R)dR, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a0f62dee03ae426245e5bbf8f91a7c2c_l3.png)
![Rendered by QuickLaTeX.com \[ A_{n - 1}(R) = \frac{d(\omega_nR^n)}{dR} = n\omega_nR^{n - 1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-22a69fcae80db387d665fc0a5d9ed4af_l3.png)
- 当
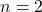 、
、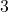 时,我们有
时,我们有
也就是说,半径为![Rendered by QuickLaTeX.com \[ 2\omega_2 = 2\pi,\; 3\omega_3 = 4\pi. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-37d364fb3dcb2051a3200c608d69745b_l3.png)
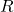 的圆周的长度为
的圆周的长度为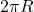 ,半径为
,半径为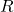 的球面的面积为
的球面的面积为