量子力学的假设
- 关于伴随算子、Hermite矩阵,可参见数值线性代数
- 由HiFi和量子力学——测不准原理,我们可以得到
- (Fourier变换)位置
 经过Fourier变换后变为
经过Fourier变换后变为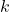 ,并且动量
,并且动量 ,所以我们可以得到位置
,所以我们可以得到位置 、动量
、动量 的Heisenberg测不准原理
的Heisenberg测不准原理 - (概率密度函数)当波函数
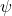 接近于粒子时,
接近于粒子时,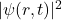 保持不变,所以我们可以认为
保持不变,所以我们可以认为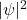 对应于粒子的概率密度函数
对应于粒子的概率密度函数
- (Fourier变换)位置
- 进一步,我们可以得到
- (测量和算子)物理量的测量值为数学期望。比如,位置
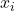 的测量值为
的测量值为
对位置![Rendered by QuickLaTeX.com \[ \mathbb{E}[x_i] = \int_{\mathbb{R}^3} x_i|\psi(r)|^2dr. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2e367ae05ace4dfa21a9abfee759933e_l3.png)
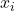 的测量对应于乘法算子
的测量对应于乘法算子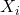 ,
,![Rendered by QuickLaTeX.com \[ X_i\psi(r) = x_i\psi(r),\; \mathbb{E}[x_i] = \langle{X_i\psi, \psi}\rangle_{L^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-276932695d5db472df1d5e045e66a375_l3.png)
- (自伴算子)对于一般的物理量,为了得到实的测量值,测量对应的线性算子
 应该满足
应该满足
在Hilbert空间![Rendered by QuickLaTeX.com \[ \langle{A\psi, \psi}\rangle_{L^2} = \overline{\langle{A\psi, \psi}\rangle_{L^2}} = \langle{\psi, A\psi}\rangle_{L^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2bcc0073bd0c28452719de7e745c1c10_l3.png)
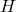 中
中
- 如果
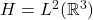 ,那么
,那么 的伴随算子
的伴随算子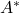 满足
满足
自伴算子满足![Rendered by QuickLaTeX.com \[ \langle{Ax, y}\rangle_{H} = \langle{x, A^*y}\rangle_{H}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9cc20179943054c086833840f4559baa_l3.png)
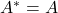
- 如果
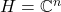 ,那么
,那么 的伴随算子
的伴随算子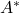 满足
满足
Hermite矩阵满足![Rendered by QuickLaTeX.com \[ \langle{Ax, y}\rangle_{H} = \langle{x, A^*y}\rangle_{H}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9cc20179943054c086833840f4559baa_l3.png)
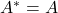
- 如果
- (测量和算子)物理量的测量值为数学期望。比如,位置
- 在无限维的自伴算子,在有限维是Hermite矩阵,所以它也叫做Hermite算子。将量子力学建立在Hilbert空间的基础之上,可以统一Schrödinger的波动力学、Heisenberg的矩阵力学
- 如果
 的特征值为
的特征值为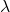 、单位特征向量为
、单位特征向量为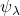 ,那么物理量在状态
,那么物理量在状态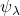 下的测量值为
下的测量值为
类似于Hermite矩阵的特征值为实数,物理量的测量值也是自伴算子的实特征值![Rendered by QuickLaTeX.com \[ \langle{A\psi_\lambda, \psi_\lambda}\rangle = \langle{\lambda\psi_\lambda, \psi_\lambda}\rangle = \lambda. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-861b4063ab5997a5de7e0096b43dd6ef_l3.png)
- 如果
Hamilton算子
- 现在我们考虑Schrödinger方程
之所以在方程中乘以![Rendered by QuickLaTeX.com \[ i\hbar\partial_t\psi = -\frac{\hbar^2}{2m}\Delta\psi. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3dd8daeda14d1fcd7696e7a0829bcdb2_l3.png)
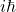 ,是因为利用Fourier变换,可得
,是因为利用Fourier变换,可得![Rendered by QuickLaTeX.com \[ \bigg(-\frac{\hbar^2}{2m}\Delta\bigg)^\wedge = \frac{\hbar^2|k|^2}{2m} = \frac{|p|^2}{2m}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6b22af2a7c80a241ce7fb61078a1fae1_l3.png)
- 由Hamilton方程可知,在相空间中,保守力场的Hamiltonian为
因此,带有势能![Rendered by QuickLaTeX.com \[ \mathcal{H} = \frac{|p|^2}{2m} + V(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ac85c26f43cba0926e2756fdcb5f56a1_l3.png)
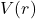 的Schrödinger方程为
的Schrödinger方程为
并且Hamilton算子为![Rendered by QuickLaTeX.com \[ i\hbar\partial_t\psi = \bigg(-\frac{\hbar^2}{2m}\Delta + V(r)\bigg)\psi, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4b84c133893133c9399d6ebf5b8f0e0b_l3.png)
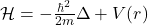
- 注意,在Hamiltonian中,
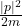 位于动量空间,
位于动量空间,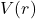 位于位置空间。因此,Hamilton算子也可以在这两个空间中表示
位于位置空间。因此,Hamilton算子也可以在这两个空间中表示
- 在位置空间中,Hamilton算子有一个微分算子、一个乘法算子
![Rendered by QuickLaTeX.com \[ \mathcal{H} = -\frac{\hbar^2}{2m}\Delta + V(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ba977aeb0a3061ea52416507dd9b414e_l3.png)
- 在动量空间中,Hamilton算子有一个乘法算子、一个卷积算子
![Rendered by QuickLaTeX.com \[ \widehat{\mathcal{H}} = \frac{|p|^2}{2m} + \widehat{V}(p / \hbar) *. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-886e4b4042e41bc4688543af728d37f5_l3.png)
- 在位置空间中,Hamilton算子有一个微分算子、一个乘法算子