参考资料:Real-Time Rendering
仿射变换
- 关于仿射变换群,可参见矩阵群
 上的仿射变换,是仿射变换群
上的仿射变换,是仿射变换群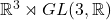 中的元素
中的元素![Rendered by QuickLaTeX.com \[ f(x) = Ax + b,\; A \in GL(3, \mathbb{R}),\; b \in \mathbb{R}^3. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-13d0564e5b1e7c190f6fa2b10be72b5c_l3.png)
 上的仿射变换,也是
上的仿射变换,也是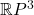 上保持无穷远超平面
上保持无穷远超平面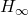 的射影变换
的射影变换![Rendered by QuickLaTeX.com \[ f\bigg(\begin{bmatrix}x \\ 1\end{bmatrix}\bigg) = \begin{bmatrix}A & b \\ 0 & 1\end{bmatrix}\begin{bmatrix}x \\ 1\end{bmatrix} = \begin{bmatrix}Ax + b \\ 1\end{bmatrix},\; \begin{bmatrix}x \\ 1\end{bmatrix} \in \mathbb{R}^3, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f88de8c1f99f391aa08ca35e0e2b0a99_l3.png)
![Rendered by QuickLaTeX.com \[ f\bigg(\begin{bmatrix}x \\ 0\end{bmatrix}\bigg) = \begin{bmatrix}A & b \\ 0 & 1\end{bmatrix}\begin{bmatrix}x \\ 0\end{bmatrix} = \begin{bmatrix}Ax \\ 0\end{bmatrix},\; \begin{bmatrix}x \\ 0\end{bmatrix} \in H_\infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9eda17362c9a890278300fe39f6e6133_l3.png)
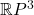 是3维实射影空间
是3维实射影空间
也就是说,![Rendered by QuickLaTeX.com \[ \mathbb{R}P^3 = (\mathbb{R}^4 - \{ 0 \})/\sim, \text{ where } v \sim \lambda v \text{ for any } \lambda \neq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-551521b5bfb473a0808c33efb78e8496_l3.png)
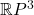 可以用4维坐标来表示(不能为原点),其中相差非零常数倍的坐标是等价的。
可以用4维坐标来表示(不能为原点),其中相差非零常数倍的坐标是等价的。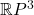 中的点是一个等价类,即
中的点是一个等价类,即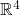 中通过原点的直线;记最后一个坐标为1的平面为
中通过原点的直线;记最后一个坐标为1的平面为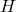 ,那么这些直线可以分为2类
,那么这些直线可以分为2类
- 一类是直线与
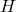 相交,得到
相交,得到 中的点。上面的第一类公式即为
中的点。上面的第一类公式即为 中的点的仿射变换
中的点的仿射变换
- 另一类是直线与
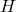 平行,得到
平行,得到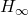 中的点。由平行性,它也可以视为
中的点。由平行性,它也可以视为 中的向量,上面的第二类公式即为
中的向量,上面的第二类公式即为 中的向量的仿射变换
中的向量的仿射变换 - 进一步,
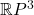 上的射影变换构成射影变换群
上的射影变换构成射影变换群
也就是说,射影变换可以由![Rendered by QuickLaTeX.com \[ PGL(4, \mathbb{R}) = GL(4, \mathbb{R})/\sim, \text{ where } A \sim \lambda A\text{ for any } \lambda \neq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f9ac915b0aeb0a4cbbf6ac641065b658_l3.png)
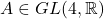 诱导,
诱导,![Rendered by QuickLaTeX.com \[ [A]: \mathbb{R}P^3 \to \mathbb{R}P^3,\; [v] \mapsto [Av]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bb5a32c9a61636520a0588ce032eff4c_l3.png)
- 一类是直线与
- 由从线性方程出发中的Gauss消元法可知,
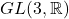 可以由初等变换生成。因此,
可以由初等变换生成。因此, 上的仿射变换可以由平移、初等变换生成,这些初等变换都有几何意义
上的仿射变换可以由平移、初等变换生成,这些初等变换都有几何意义
- 平移(Translation)
![Rendered by QuickLaTeX.com \[ \begin{bmatrix}1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-15121101addf59d00b53a2e4de39f561_l3.png)
- 伸缩(Scaling)
![Rendered by QuickLaTeX.com \[ \begin{bmatrix}s & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-308cf500f44cb950f2106330db08c4d8_l3.png)
- 切变(Shearing)
![Rendered by QuickLaTeX.com \[ \begin{bmatrix}1 & s & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9ac59856e6bf0ed2f4e3b191996fd37e_l3.png)
- 镜面反射(Mirror Reflection)
![Rendered by QuickLaTeX.com \[ \begin{bmatrix}0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c7b780285a570692b98419ea308b42b1_l3.png)
- 平移(Translation)
刚体变换
- 关于刚体变换群,可参见矩阵群
 赋予典范Riemann度量,成为一个Riemann流形
赋予典范Riemann度量,成为一个Riemann流形![Rendered by QuickLaTeX.com \[ g_{can}(v, w) = v_1w_1 + v_2w_2 + v_3w_3. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-54634bbabdbf4de2035fa38b537c3d6f_l3.png)
 上的刚体变换,是保持定向的等距变换群
上的刚体变换,是保持定向的等距变换群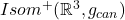 中的元素
中的元素
- 一方面,刚体变换群满足
![Rendered by QuickLaTeX.com \[ SE(3, \mathbb{R}) = \mathbb{R}^3 \rtimes SO(3, \mathbb{R}) \subset Isom^+(\mathbb{R}^3, g_{can}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-033248487b3fa04931c0d89a5afb015a_l3.png)
- 另一方面,由Riemann几何的结果可知,
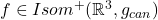 可以由其1阶展开确定,
可以由其1阶展开确定,
从而,![Rendered by QuickLaTeX.com \[ f(x) = f(0) + df_0 \cdot x,\; df_0 \in SO(3, \mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c5c7f9fd7ad8e2837d06111081f4ed19_l3.png)
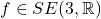 。因此,
。因此, 上的刚体变换,也是刚体变换群
上的刚体变换,也是刚体变换群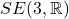 中的元素
中的元素
- 一方面,刚体变换群满足
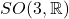 中的元素都是绕某条直线的旋转(Rotation),从而
中的元素都是绕某条直线的旋转(Rotation),从而 上的刚体变换可以由平移、绕某条直线的旋转生成
上的刚体变换可以由平移、绕某条直线的旋转生成
- 设
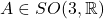 。那么,
。那么,
即![Rendered by QuickLaTeX.com \[ \det(A - I) = \det(A^T(A - I)) = \det(I - A^T) = (-1)^3\det(A - I), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-20291ab31a163fbe00e91e0e04715123_l3.png)
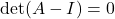 。因此,线性方程
。因此,线性方程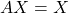 存在非零解
存在非零解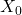 ,从而
,从而 保持
保持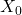 方向的直线
方向的直线 不变
不变 - 同时,
 在与
在与 正交的2维平面上,也是保持定向的等距变换,并且保持原点不变,所以是
正交的2维平面上,也是保持定向的等距变换,并且保持原点不变,所以是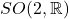 中的元素。由四元数可知,
中的元素。由四元数可知,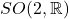 中的元素是绕原点的旋转,所以
中的元素是绕原点的旋转,所以 是绕直线
是绕直线 的旋转
的旋转
- 设
- 由数值线性代数中的奇异值分解可知,
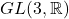 可以由对角元素为正的对角矩阵、
可以由对角元素为正的对角矩阵、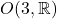 生成。由矩阵群可知,
生成。由矩阵群可知,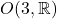 可以由
可以由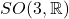 、一个行列式为-1的矩阵生成
、一个行列式为-1的矩阵生成
- 对角元素为正的对角矩阵 –> 对角元素为正的伸缩
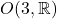 –> 旋转、镜面反射
–> 旋转、镜面反射
- 因此,我们也可以将上面的伸缩更换为对角元素为正的伸缩,将上面的切变更换为旋转。在计算机图形学中,旋转通常用四元数来表示
四元数和旋转
- 关于四元数,可参见四元数
- 四元数的集合
 可以视为
可以视为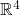 ,并且可以分解为实部(基底为1,可以视为
,并且可以分解为实部(基底为1,可以视为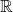 )、虚部(基底为
)、虚部(基底为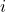 、
、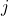 、
、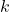 ,可以视为
,可以视为 )。只有实部的四元数为实数,只有虚部的四元数为纯虚数
)。只有实部的四元数为实数,只有虚部的四元数为纯虚数 - 设
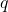 为四元数,
为四元数,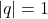 。定义
。定义
那么,![Rendered by QuickLaTeX.com \[ f_q: \mathbb{H} \to \mathbb{H}, x \mapsto qxq^{-1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-084ae400c6c540e7fbb292a4232e5304_l3.png)
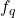 为
为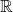 -线性变换,并且保持1不变,从而保持实数不变。因此,我们只需考虑纯虚数的情形,并且将
-线性变换,并且保持1不变,从而保持实数不变。因此,我们只需考虑纯虚数的情形,并且将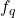 视为
视为 上的
上的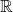 -线性变换
-线性变换 - 模长为1的纯虚数具有良好的性质。设
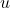 、
、 为模长为1的纯虚数,那么
为模长为1的纯虚数,那么
同时,![Rendered by QuickLaTeX.com \[ u^{-1} = \overline{u} = -u,\; v^{-1} = \overline{v} = -v,\; u^2 = v^2 = -1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-da1927bd9b26826b4d99ecbf7960478c_l3.png)
在最后一步,我们将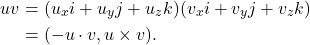
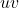 视为
视为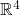 中的向量,将
中的向量,将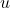 、
、 视为
视为 中的向量。因此,模长为1的纯虚数的乘法,实部相当于向量的内积,虚部相当于向量的外积
中的向量。因此,模长为1的纯虚数的乘法,实部相当于向量的内积,虚部相当于向量的外积 - 将
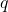 分解为实部、虚部,
分解为实部、虚部,
其中,![Rendered by QuickLaTeX.com \[ q = \cos(\phi) + \sin(\phi)u,\; q^{-1} = \overline{q} = \cos(\phi) - \sin(\phi)u, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2e4cacf4a1ee64f231213d6e538cf9ac_l3.png)
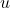 为模长为1的纯虚数。计算
为模长为1的纯虚数。计算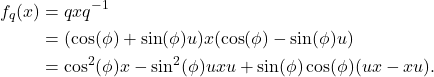
- 由
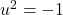 可知,
可知,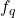 保持
保持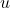 不变,从而保持
不变,从而保持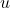 方向的直线
方向的直线 不变
不变 - 同时,在与
 正交的2维平面上,任取一个模长为1的纯虚数
正交的2维平面上,任取一个模长为1的纯虚数 。利用
。利用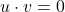 ,可得
,可得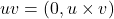 ,它也是模长为1的纯虚数,并且对应于
,它也是模长为1的纯虚数,并且对应于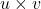 。由此可知,
。由此可知,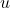 、
、 、
、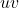 构成右手坐标系,并且
构成右手坐标系,并且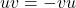 。因此,
。因此,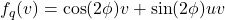 将
将 绕直线
绕直线 旋转
旋转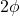
- 由
计算机图形学的MVP变换
- 计算机图形学可以将
 中的模型渲染为
中的模型渲染为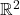 中的图像,其原理类似于相机拍摄模型的照片
中的图像,其原理类似于相机拍摄模型的照片 - 模型(Model)变换是一个仿射变换(模型 –> M –> 世界空间)
- 模型变换可以让我们将模型设置为合适的位置(平移)、合适的大小(伸缩)、合适的角度(旋转)
- 视觉(View)变换是一个仿射变换(世界空间 –> V –> 视觉空间)
- 视觉变换可以让我们获得在相机的位置和角度,人眼所见的原风景
- 设相机的位置(Eye)为
 ,相机对准的方向(Gaze)为
,相机对准的方向(Gaze)为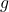 ,相机朝上的方向(Top)为
,相机朝上的方向(Top)为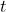 。首先,我们使用一个平移,将相机的位置变为原点
。首先,我们使用一个平移,将相机的位置变为原点![Rendered by QuickLaTeX.com \[ \begin{bmatrix}1 & 0 & 0 & -e_x \\ 0 & 1 & 0 & -e_y \\ 0 & 0 & 1 & -e_z \\ 0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}e_x \\ e_y \\ e_z \\ 1\end{bmatrix} = \begin{bmatrix}0 \\ 0 \\ 0 \\ 1\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e707a05a154613fea218bd3f34520f4c_l3.png)
- 其次,我们使用一个旋转,将
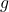 变为
变为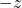 轴,将
轴,将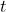 变为
变为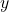 轴,将
轴,将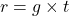 变为
变为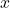 轴。之所以取
轴。之所以取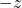 轴,是因为在右手坐标系中,如果人眼所见为
轴,是因为在右手坐标系中,如果人眼所见为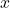 轴水平向右、
轴水平向右、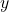 轴垂直向上,那么
轴垂直向上,那么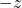 轴的方向是人眼所见的方向
轴的方向是人眼所见的方向![Rendered by QuickLaTeX.com \[ \begin{bmatrix}r_x & r_y & r_z & 0 \\ t_x & t_y & t_z & 0 \\ -g_x & -g_y & -g_z & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}r_x & t_x & g_x \\ r_y & t_y & g_y \\ r_z & t_z & g_z \\ 0 & 0 & 0\end{bmatrix} = \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 0\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0b2818373839a47d4a32253ebbab835a_l3.png)
- 投影(Projection)变换是一个射影变换(视觉空间 –> P –> 照片)
- 投影变换可以让我们从3维降低到2维
- 在相机拍摄模型的照片时,人眼所见的原风景并不是整个
 ,而是一个有限的视觉体积(View Volume)。根据透视原理,我们可以取视觉体积为从原点出发的锥体
,而是一个有限的视觉体积(View Volume)。根据透视原理,我们可以取视觉体积为从原点出发的锥体 - 因为我们拍摄的照片通常是矩形的,所以我们让锥体的底面为矩形。因为视觉体积有限,所以我们用一个较远的平面来截断锥体,得到远底面;因为人眼位于原点,所以我们取一个较近的平面作为照片,得到近底面,然后投影到其上
- 设近底面、远底面的
 坐标分别为
坐标分别为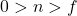 。对于近底面
。对于近底面 、远底面
、远底面 之间的所有模型上的点
之间的所有模型上的点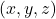 ,我们都使用透视将其投影到近底面
,我们都使用透视将其投影到近底面 上,
上,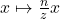 ,
,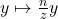 。这无法用仿射变换来实现,原因是
。这无法用仿射变换来实现,原因是 坐标是变量,故我们使用射影变换
坐标是变量,故我们使用射影变换
取![Rendered by QuickLaTeX.com \[ \begin{bmatrix}n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ * & * & * & * \\ 0 & 0 & 1 & 0\end{bmatrix}\begin{bmatrix}x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix}nx \\ ny \\ * \\ z \end{bmatrix} \sim \begin{bmatrix}\frac{nx}{z} \\ \frac{ny}{z} \\ * \\ 1 \end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a72685eccd9af3c1fc0248c1eb25c412_l3.png)
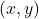 坐标而忽略
坐标而忽略 坐标,即可得到想要的照片
坐标,即可得到想要的照片
- 因为近的模型会挡住远的模型,所以
 坐标用于判断模型的远近
坐标用于判断模型的远近
- 如果我们让射影变换保持近底面
 、远底面
、远底面 不变,并且
不变,并且 坐标与
坐标与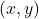 坐标无关,那么我们可以得到完整的射影变换
坐标无关,那么我们可以得到完整的射影变换
并非所有模型上的![Rendered by QuickLaTeX.com \[ \begin{bmatrix}n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -nf \\ 0 & 0 & 1 & 0\end{bmatrix}\begin{bmatrix}x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix}nx \\ ny \\ (n + f)z - nf \\ z \end{bmatrix} \sim \begin{bmatrix}\frac{nx}{z} \\ \frac{ny}{z} \\ n + f - \frac{nf}{z} \\ 1 \end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c3c734e09407edd2829874f3ce55e6ec_l3.png)
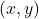 坐标都会出现在照片上,只有对应的
坐标都会出现在照片上,只有对应的 坐标距离原点最近才行(由于
坐标距离原点最近才行(由于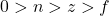 ,这需要
,这需要 最大)
最大)
- 如果我们让射影变换保持近底面