浮点数
- 浮点数格式
- 基数
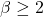
- 精度
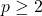
- 最小指数
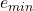 、最大指数
、最大指数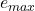
- 在实际的浮点数格式中,
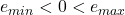 。在IEEE 754中,
。在IEEE 754中,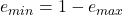
- 基数
- 在上面的浮点数格式中,浮点数至少具有一种表示
![Rendered by QuickLaTeX.com \[ x = M \cdot \beta^{e - p + 1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-666bce7519b254342b5055df2ee2bf98_l3.png)
 为整数的有效数字,
为整数的有效数字,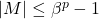
 为整数的指数,
为整数的指数,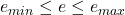
- //
IEEE754-2008
- 浮点数格式
- 基数
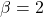 ,或者
,或者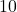
- 最小指数、最大指数
![Rendered by QuickLaTeX.com \[ e_{min} = 1 - e_{max}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-683161fb9b25ed8e1807b579374b8284_l3.png)
- 基数
- 二进制交换格式
- 16位
![Rendered by QuickLaTeX.com \[ p = 11,\; e_{min} = -14,\; e_{max} = +15. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-58fa796a51f3cf94c534c783748ebd5c_l3.png)
- 32位,单精度
![Rendered by QuickLaTeX.com \[ p = 24,\; e_{min} = -126,\; e_{max} = +127. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a6bb26ea557dff2e74208da19dab661d_l3.png)
- 64位,双精度
![Rendered by QuickLaTeX.com \[ p = 53,\; e_{min} = -1022,\; e_{max} = +1023. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1e3ba149a80d2f7765f5fe4b65c5602a_l3.png)
- 128位
![Rendered by QuickLaTeX.com \[ p = 113,\; e_{min} = -16382,\; e_{max} = +16383. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a0d1f86aa329e0d21302a63d8ae438ee_l3.png)
- 16位
- 二进制编码
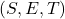
- 1位符号
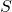 ,
,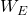 位指数
位指数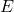 ,
,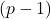 位尾部有效数字
位尾部有效数字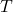
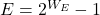 ,
,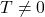
- NaN(Not a Number,非数)
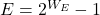 ,
,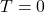
- 无穷大
![Rendered by QuickLaTeX.com \[ (-1)^S \times (+\infty). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1f13dc88d0435969d84255d0f8d74835_l3.png)
- 无穷大
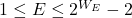
- 规范化浮点数
![Rendered by QuickLaTeX.com \[ (-1)^S \times 2^{E - b} \times (1 + T \cdot 2^{1 - p}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-114919887113d534e88d92c46e9acda9_l3.png)
- 指数偏移为
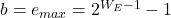
- 规范化浮点数
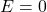 ,
,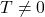
- 非规范化浮点数
![Rendered by QuickLaTeX.com \[ (-1)^S \times 2^{e_{min}} \times (0 + T \cdot 2^{1 - p}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6b805e77f7625a7b5acc0b970c6b32e4_l3.png)
- 非规范化浮点数
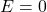 ,
,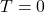
- 零
![Rendered by QuickLaTeX.com \[ (-1)^S \times (+0). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9306ac4e87fab40365daac6b668f063e_l3.png)
- 零
- 1位符号