命题逻辑
- 归纳(Induction)、演绎(Deduction)是同一公理系统的不同表现
- 归纳是从特殊结论到一般结论,比如归纳定义、结构归纳法
- 演绎是从一般结论到特殊结论,比如推理规则、演绎树
- 在从不动点定理到编程语言中,我们考虑归纳。在这里,我们考虑演绎
- 命题逻辑的语言
- 字母表
- (命题变量)
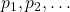
- (连词)
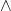 、
、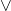 、
、 、
、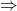
- (括号)
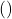
- 我们可以将
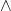 、
、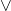 、
、 、
、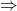 分别视为与、或、非、推出。不过,我们应该用形式化的方式来演算
分别视为与、或、非、推出。不过,我们应该用形式化的方式来演算
- (命题变量)
- 公式,归纳定义
- 命题变量是公式
- 如果
 、
、 是公式,那么
是公式,那么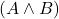 、
、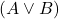 、
、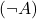 、
、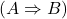 也是公式
也是公式
- 字母表
- 命题逻辑的公理系统
- 公理
- (公理1)
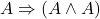
- (公理2)
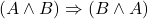
- (公理3)
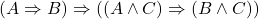
- (公理4)
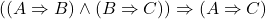
- (公理5)
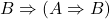
- (公理6)
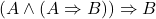
- //
- (公理7)
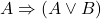
- (公理8)
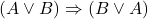
- (公理9)
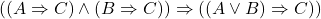
- //
- (公理10)
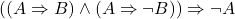
- (公理1)
- 推理规则
- 如果
 成立,并且
成立,并且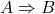 成立,那么
成立,那么 成立。这称为假言推理(Modus Ponens,MP),它类似于Aristotle的三段论
成立。这称为假言推理(Modus Ponens,MP),它类似于Aristotle的三段论![Rendered by QuickLaTeX.com \[ \dfrac{A \quad A \Rightarrow B}{B} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-632e5f372d7dc95ce87329e4bcd2cfe6_l3.png)
- 如果
- 公理
从公理出发
- 导出过程(Derivation)是一列公式
 ,其中
,其中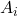 ,
,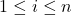 为下面两种情形之一
为下面两种情形之一
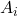 为公理
为公理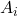 由前面的公式、MP得到
由前面的公式、MP得到- 如果
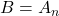 ,那么
,那么 称为定理(Theorem)。因为导出过程给出了
称为定理(Theorem)。因为导出过程给出了 的证明(Proof),所以
的证明(Proof),所以 也称为可证明的(Provable),记为
也称为可证明的(Provable),记为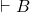
- 我们只有一个推理规则MP,如果直接从公理出发,那么导出过程会非常繁琐。因此,我们可以先建立一些中间结论,即引理(Lemma)。比如
- (
 -引入)如果
-引入)如果 、
、 成立,那么
成立,那么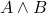 成立
成立
- 1.(假设)

- 2.(公理5)
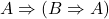
- 3.(MP 1、2)
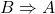
- 4.(公理3)
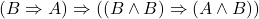
- 5.(MP 3、4)
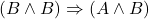
- //
- 6.(假设)

- 7.(公理1)
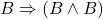
- 8.(MP 6、7)
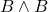
- 9.(MP 5、8)
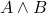
- 1.(假设)
- (
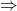 -传递)如果
-传递)如果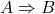 、
、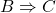 成立,那么
成立,那么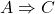 成立
成立
- 1.(假设)
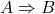
- 2.(假设)
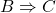
- 3.(
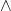 -引入)
-引入)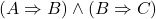
- 4.(公理4)
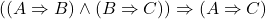
- 5.(MP 3、4)
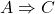
- 1.(假设)
- 利用
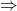 -传递,我们可以更方便地证明定理
-传递,我们可以更方便地证明定理
- (
- (定理1)
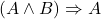
- 1.(公理5)
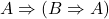
- 2.(公理3)
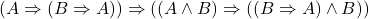
- 3.(MP 1、2)
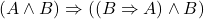
- 4.(公理2)
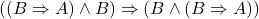
- 5.(
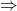 -传递 3、4)
-传递 3、4)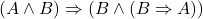
- 6.(公理6)
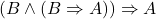
- 7.(
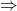 -传递 5、6)
-传递 5、6) 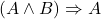
- 1.(公理5)
- 定理1的导出过程等价于如下的演绎树,令
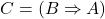
![Rendered by QuickLaTeX.com \[ \dfrac{\dfrac{\dfrac{Ax5 \quad Ax3}{(A \wedge B) \Rightarrow (C \wedge B)} \quad \dfrac{}{(C \wedge B) \Rightarrow (B \wedge C)}}{(A \wedge B) \Rightarrow (B \wedge C)} \quad \dfrac{}{(B \wedge C) \Rightarrow A}}{(A \wedge B) \Rightarrow A} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f1472c62d32820db9c263cbf6f70941d_l3.png)
从假设出发的导出过程
- 在建立上面的引理时,我们实际上使用了从假设出发的导出过程(Derivation from Assumptions),它在导出过程中,增加了
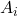 属于假设
属于假设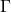 的情形
的情形
- 如果
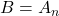 ,那么
,那么 称为(从
称为(从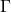 出发)可导出的(Derivable),记为
出发)可导出的(Derivable),记为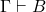
- 如果
 为可证明的,那么
为可证明的,那么 为可导出的,此时
为可导出的,此时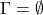
- 如果
- 基本性质
- (公理)如果
 为公理,那么
为公理,那么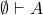
- (假设)如果
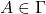 ,那么
,那么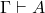
- (减弱)如果
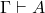 ,
,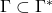 ,那么
,那么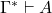
- (MP)如果
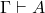 ,
,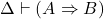 ,那么
,那么
- 我们有从
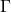 、
、 出发的导出过程
出发的导出过程![Rendered by QuickLaTeX.com \[ A_1, \ldots, A_n = A,\; B_1, \ldots, B_m = (A \Rightarrow B). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d488de54897478f8645526c3f0987099_l3.png)
- 因此,我们有从
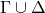 出发的导出过程
出发的导出过程![Rendered by QuickLaTeX.com \[ A_1, \ldots, A_n,\; B_1, \ldots, B_m,\; B. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d7298993eb78d83121989ec3e7bdf061_l3.png)
- 我们有从
- 类似地,我们可以得到
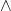 -引入、
-引入、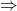 -传递
-传递
- (公理)如果
- (演绎定理,Deduction Theorem)如果
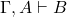 ,那么
,那么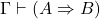
- 我们有从
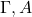 出发的导出过程
出发的导出过程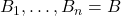 。对
。对 使用数学归纳法
使用数学归纳法 - 当
 时,我们有如下3种情形
时,我们有如下3种情形
 为公理
为公理
- 1.(公理)
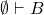
- 2.(公理5)
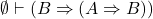
- 3.(MP 1、2)
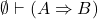
- 4.(减弱)
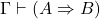
- 1.(公理)
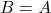
- 1.(公理1、定理1)
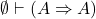
- 2.(减弱)
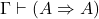
- 1.(公理1、定理1)
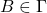
- 1.(假设)
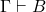
- 2.(公理5)
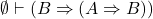
- 3.(MP 1、2)
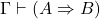
- 1.(假设)
- 如果对于小于
 的情形成立,那么考虑
的情形成立,那么考虑 的情形。我们需要使用一个可证明的定理
的情形。我们需要使用一个可证明的定理![Rendered by QuickLaTeX.com \[ \emptyset \vdash (A \Rightarrow (B \Rightarrow C)) \Rightarrow ((A \Rightarrow B) \Rightarrow (A \Rightarrow C)) \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8b815b5791d6fdfff1018117e7a70f96_l3.png)
- 如果
 为公理、
为公理、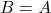 、
、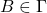 ,那么由上述可知,
,那么由上述可知,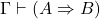
- 如果
 由MP得到,那么存在
由MP得到,那么存在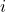 、
、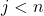 ,使得
,使得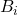 、
、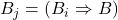
- 1.(归纳假设)
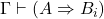
- 2.(归纳假设)
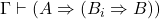
- 3.(一个可证明的定理)
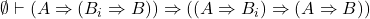
- 4.(MP 2、3)
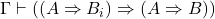
- 5.(MP 1、4)
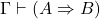
- 1.(归纳假设)
- 如果
- 我们有从
公理系统的独立性
- Hilbert认为,公理系统应该满足如下条件。对于
 、
、 ,可证明的公式数量记为
,可证明的公式数量记为
- (相容性)

- (完备性)
- (独立性)一条公理不能由其余公理导出
- (相容性)
- 公理系统的例子
- 算术的公理系统具有相容性。然而,由Gödel不完备定理可知,算术的公理系统不具有完备性
- Euclid几何的公理系统具有独立性。其中,平行公设不能由其他公设导出,这可以通过构造非Euclid几何的模型得到。关于平行公设,可参见从Euclid几何到非Euclid几何
- 因此,我们既需要考虑证明论(Proof Theory),也需要考虑模型论(Model Theory)
- 之前,我们讨论的公理系统为最小逻辑系统
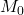 ,它关于
,它关于 只有一个公理
只有一个公理
- (公理10)
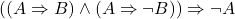
- (公理10)
- 现在,我们添加关于
 的公理
的公理