偏序关系
- 集合
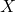 上的偏序关系
上的偏序关系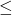 满足如下条件。对任意
满足如下条件。对任意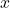 、
、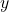 、
、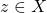 ,
,
- (自反性)
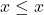
- (反对称性)如果
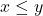 ,
,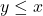 ,那么
,那么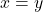
- (传递性)如果
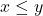 ,
,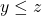 ,那么
,那么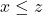
- (自反性)
- 设
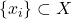 为序列,
为序列, 为映射
为映射
- 如果
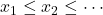 ,那么
,那么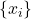 称为递增序列
称为递增序列 - 如果对任意
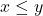 ,我们有
,我们有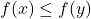 ,那么
,那么 称为递增映射
称为递增映射
- 如果
- 设
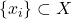 为递增序列,
为递增序列, 为递增映射
为递增映射
- 如果
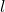 为
为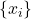 的最小上界,那么它称为
的最小上界,那么它称为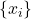 的极限,记为
的极限,记为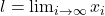
- 如果对任意递增序列
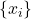 ,我们有
,我们有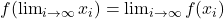 ,那么
,那么 称为连续映射
称为连续映射
- 如果
- 注意,在连续映射的定义中,未必每个递增序列都有极限。如果每个递增序列都有最小上界,那么
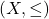 称为弱完备空间,连续映射需要定义在弱完备空间中
称为弱完备空间,连续映射需要定义在弱完备空间中
进一步,如果每个子集 都有最小上界(记为
都有最小上界(记为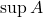 ,称为上确界),那么
,称为上确界),那么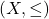 称为强完备空间。强完备空间是弱完备空间,原因是递增序列是子集
称为强完备空间。强完备空间是弱完备空间,原因是递增序列是子集 - 强完备空间
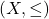 的每个子集
的每个子集 都有最大下界(记为
都有最大下界(记为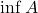 ,称为下确界)
,称为下确界)
- 设
为![Rendered by QuickLaTeX.com \[ B = \{ y \in X : y \leq x \text{ for any } x \in A \} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1a9af6f7dfea1ab697db936882bfc4b3_l3.png)
 的下界构成的集合。由
的下界构成的集合。由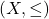 的强完备性,可取
的强完备性,可取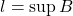
- 对任意
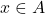 ,
,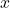 为
为 的上界。由上确界的最小性,可得
的上界。由上确界的最小性,可得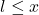 。也就是说,
。也就是说,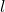 为
为 的下界
的下界 - 如果
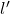 为
为 的另一个下界,那么
的另一个下界,那么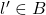 。由上确界是上界,可得
。由上确界是上界,可得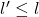
- 设
- 设
 为集合,
为集合,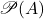 为
为 的幂集,
的幂集,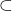 为“包含”关系。
为“包含”关系。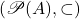 是弱完备的,原因是每个递增序列
是弱完备的,原因是每个递增序列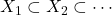 都有极限
都有极限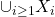
进一步,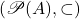 是强完备的,原因是每个子集
是强完备的,原因是每个子集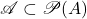 都有最小上界
都有最小上界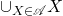
不动点定理
- (第一不动点定理)设
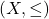 为弱完备空间。如果
为弱完备空间。如果 连续,并且
连续,并且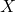 有最小元素
有最小元素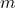 ,那么如下的迭代方法给出了
,那么如下的迭代方法给出了 的最小不动点
的最小不动点![Rendered by QuickLaTeX.com \[ p = \lim_{i \to \infty} f^i(m). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-86e01f279c6b051ed5a7e3aa67abeaa1_l3.png)
 为不动点:
为不动点:
- 因为
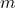 为最小元素,
为最小元素, 递增,所以
递增,所以
由![Rendered by QuickLaTeX.com \[ m \leq f(m) \leq \cdots \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5e3473d8d386f304ca954198b0effc57_l3.png)
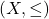 的弱完备性,递增序列
的弱完备性,递增序列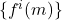 有极限
有极限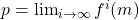
- 由于
 连续,故
连续,故![Rendered by QuickLaTeX.com \[ f(p) = f(\lim_{i \to \infty} f^i(m)) = \lim_{i \to \infty} f^{i + 1}(m) = p. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-59a237f85db640fa26a66cfadf8a2f59_l3.png)
- 因为
 为最小不动点:
为最小不动点:
- 如果
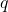 为另一个不动点,那么
为另一个不动点,那么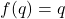 ,并且
,并且
也就是说,![Rendered by QuickLaTeX.com \[ m \leq q,\; f(m) \leq f(q) = q,\; \ldots \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b3bd5cec393a79a30d59bc04ac43aa00_l3.png)
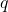 为
为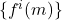 的上界。由极限的最小性,可得
的上界。由极限的最小性,可得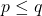
- 如果
- (第二不动点定理)设
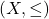 为强完备空间。如果
为强完备空间。如果 递增,那么如下的下确界方法给出了
递增,那么如下的下确界方法给出了 的最小不动点
的最小不动点![Rendered by QuickLaTeX.com \[ p = \inf A, \text{ where } A = \{ x \in X : f(x) \leq x \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-31571ff39ea96616446f1b4e6d6e5bc3_l3.png)
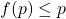 :
:
- 对任意
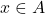 ,由于
,由于 递增,故
递增,故
也就是说,![Rendered by QuickLaTeX.com \[ p \leq x \Rightarrow f(p) \leq f(x) \leq x. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9bc640a8020670e60cede73ec0746aff_l3.png)
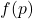 为
为 的一个下界。由下确界的最大性,可得
的一个下界。由下确界的最大性,可得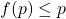
- 对任意
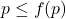 :
:
- 由于
 递增,故
递增,故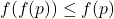 。也就是说,
。也就是说,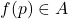 。由下确界是下界,可得
。由下确界是下界,可得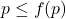
- 由于
 为最小不动点:
为最小不动点:
- 如果
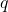 为另一个不动点,那么
为另一个不动点,那么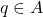 。由下确界是下界,可得
。由下确界是下界,可得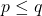
- 如果
从不动点定理到编程语言
- 编程语言源于归纳定义,归纳定义源于不动点定理
- 归纳定义
- 设
 为集合,
为集合,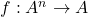 为映射。如果子集
为映射。如果子集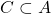 满足
满足
那么![Rendered by QuickLaTeX.com \[ x_1, \ldots, x_n \in C \Rightarrow f(x_1, \ldots, x_n) \in C, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-79efd8e4b82346cbf5133ced2c4e1455_l3.png)
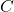 称为在
称为在 下封闭
下封闭
- 进一步,如果
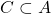 是在
是在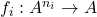 ,
,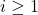 下封闭的最小子集,那么
下封闭的最小子集,那么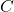 由
由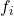 归纳定义
归纳定义
- 设
- 归纳定义的存在性
- 定义
那么![Rendered by QuickLaTeX.com \[ F: \mathscr{P}(A) \to \mathscr{P}(A),\; F(X) = \cup_{i \geq 1} f_i(X^{n_i}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cbd8241330319018da11d3702ea09652_l3.png)
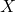 在
在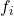 ,
,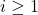 下封闭当且仅当
下封闭当且仅当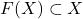
- 由上面的笔记,
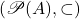 是强完备的。进一步,
是强完备的。进一步, 递增。因此,我们可以使用第二不动点定理,得到
递增。因此,我们可以使用第二不动点定理,得到 的最小不动点
的最小不动点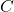
注意,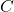 也是在
也是在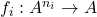 ,
,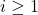 下封闭的最小子集,原因是
下封闭的最小子集,原因是![Rendered by QuickLaTeX.com \[ C = \inf \mathscr{A}, \text{ where } \mathscr{A} = \{ X \in \mathscr{P}(A) : F(X) \subset X \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dda814ddcf220b5d08370f0be635e360_l3.png)
- 我们也可以使用第一不动点定理。注意到
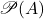 有最小元素
有最小元素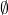 ,并且
,并且 连续,
连续,
因此,![Rendered by QuickLaTeX.com \[ F(\cup_{j \geq 1} X_j) = \cup_{i, j \geq 1} f_i(X_j^{n_i}) = \cup_{j \geq 1} F(X_j). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-015e348b86f6727cf82ef6b682bed00e_l3.png)
为了得到![Rendered by QuickLaTeX.com \[ C = \lim_{i \to \infty} F^i(\emptyset) = \cup_{i \geq 1} F^i(\emptyset). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c7633492300ff93044f8430f31f95c52_l3.png)
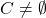 ,某些
,某些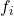 必须将空集
必须将空集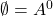 映射到非空集
映射到非空集
- 定义
- 归纳定义的第一个作用是定义递归结构,比如设
 为
为 、
、 、
、 的字符串构成的集合。那么,
的字符串构成的集合。那么,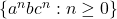 的归纳定义为
的归纳定义为
如果我们将![Rendered by QuickLaTeX.com \[ f_1: \emptyset \to A,\; \mapsto b.\quad f_2: A \to A,\; t \mapsto atc. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8b7208b491c84ffae4bafdf333b2acaa_l3.png)
 视为左括号、将
视为左括号、将 视为右括号,那么上面定义了一种嵌套括号的语言
视为右括号,那么上面定义了一种嵌套括号的语言 - 归纳定义的第二个作用是对递归结构进行证明。在数理逻辑和计算机科学中,
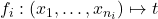 称为推理规则,记为
称为推理规则,记为
这里,![Rendered by QuickLaTeX.com \[ \dfrac{x_1 \ldots x_{n_i}}{t} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c8d844ad6c2b0cc1f712049cac27d302_l3.png)
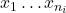 为前提,
为前提,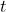 为结论。没有前提的推理规则称为公理。比如
为结论。没有前提的推理规则称为公理。比如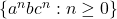 的推理规则为
的推理规则为![Rendered by QuickLaTeX.com \[ \dfrac{}{b} \quad \dfrac{t}{atc} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-23648533f89193be411f93d999e80e95_l3.png)
- 首先,我们可以利用推理规则证明
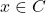 。注意,
。注意,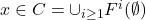 等价于
等价于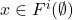 对某个
对某个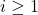 成立,所以我们只需构造一个从公理出发的、有限的推理规则链,比如
成立,所以我们只需构造一个从公理出发的、有限的推理规则链,比如
在一般情况下,这会构成一棵树,称为演绎树![Rendered by QuickLaTeX.com \[ \dfrac{}{\dfrac{b}{\dfrac{abc}{aabcc}}} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-106e5804c49cb5732112b632d034010e_l3.png)
- 其次,我们可以对推理规则使用结构归纳法。如果
 具有性质
具有性质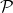 可以推出
可以推出 具有性质
具有性质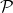 ,
,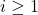 ,那么整个
,那么整个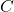 也具有性质
也具有性质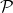
- 令
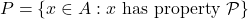
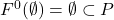 。如果
。如果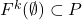 ,那么对任意
,那么对任意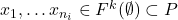 ,由条件可知,
,由条件可知,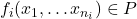 ,
,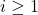 。因此,
。因此,
由数学归纳法,![Rendered by QuickLaTeX.com \[ F^{k + 1}(\emptyset) = \cup_{i \geq 1} f_i(F^k(\emptyset)^{n_i}) \subset P. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-57fc4e2261915afe30a97e19d8eb989c_l3.png)
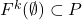 ,
, 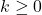 ,故
,故![Rendered by QuickLaTeX.com \[ C = \cup_{i \geq 1} F^i(\emptyset) \subset P. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9e6364f89a6a34c742fd5ceaeb87f19f_l3.png)
- 令
- 结构归纳法是数学归纳法的一种推广形式,原因是数学归纳法是如下推理规则的结构归纳法
![Rendered by QuickLaTeX.com \[ \dfrac{}{0} \quad \dfrac{n}{n + 1} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b03b0ed3c02e66141cb2f9015d09c83d_l3.png)