参考资料:Lambda Calculus with Types
给Lambda项增加类型
- 类似于编程视角下的范畴和函子,我们让变量具有对象的类型,让函数具有箭头的类型。这样,只有函数(箭头的类型)应用于变量(对象的类型)是合法的
- 简单类型的集合
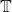
- (对象)如果
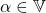 ,那么
,那么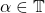
- (箭头)如果
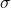 、
、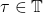 ,那么
,那么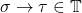
- (对象)如果
- Lambda项的类型
- (变量)
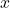 具有唯一的类型
具有唯一的类型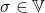 ,记为
,记为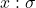
- (抽象)如果
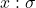 、
、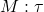 ,那么
,那么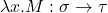
- (应用)如果
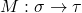 、
、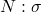 ,那么
,那么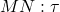
- (变量)
- 注意,并非所有Lambda项都具有类型(比如变量应用于变量)。如果一个Lambda项具有类型,那么它称为可类型化的Lambda项
类型论的三个问题
- 可类型化(Typability)
- 类型检查(Type Checking)
- 寻找项(Term Finding)