音乐的五线谱
- 关于音乐,可参见图解和声。关于时频分析,可参见频率响应和采样率
- 在音乐的五线谱中
- 水平方向表示时间(音符的时值),时间上的变化是音乐的节奏(Rhythm)
- 垂直方向表示频率(音符的音高),频率上的变化是音乐的曲调(Tune)
- 进一步,节奏、曲调的结合是旋律(Melody)
- 按照时频分析的观点
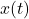 是信号的时域特征,它对应于音乐的节奏
是信号的时域特征,它对应于音乐的节奏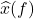 是信号的频域特征,它对应于音乐的曲调
是信号的频域特征,它对应于音乐的曲调
- 人在听音乐时,能够同时感知到节奏、曲调的结合(即旋律),所以我们需要同时对时域和频域进行分析。在理想情形下,我们应该得到时间
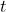 的频率
的频率 ,也就是信号的瞬时频率。然而,测不准原理指出,我们无法测量出信号的瞬时频率。因此,绝对的HiFi(High Fidelity,高保真)是无法实现的
,也就是信号的瞬时频率。然而,测不准原理指出,我们无法测量出信号的瞬时频率。因此,绝对的HiFi(High Fidelity,高保真)是无法实现的
时频分析中的测不准原理
- 设
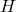 为Hilbert空间,
为Hilbert空间, 、
、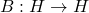 为自伴算子。那么,对于任意
为自伴算子。那么,对于任意 、
、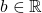 ,我们有
,我们有![Rendered by QuickLaTeX.com \[ \frac 12|\langle{[A, B]f, f}\rangle_H| \leq ||(A - a)f||_H \cdot ||(B - b)f||_H. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dfc3b573eafff841f5b8d935c747af9b_l3.png)
 、
、 的Poisson括号为
的Poisson括号为![Rendered by QuickLaTeX.com \[ [A, B] = AB - BA = (A - a)(B - b) - (B - b)(A - a). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-eb7af19d94934cadbf483c3d0f7c1d40_l3.png)
- 由于
 、
、 为自伴算子,故
为自伴算子,故
由Cauchy-Schwartz不等式,可得![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \langle{[A, B]f, f}\rangle_H &= \langle{(A - a)(B - b)f, f}\rangle_H - \langle{(B - b)(A - a)f, f}\rangle_H \\ &= \langle{(B - b)f, (A - a)f}\rangle_H - \langle{(A - a)f, (B - b)f}\rangle_H \\ &= 2iIm\langle{(B - b)f, (A - a)f}\rangle_H. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-35834be3fa91bc6975d66b5267991b60_l3.png)
![Rendered by QuickLaTeX.com \[ |\langle{[A, B]f, f}\rangle_H| \leq 2||(A - a)f||_H \cdot ||(B - b)f||_H. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-00b8f195d14757be195c1bb1a0691a0d_l3.png)
- 考虑如下的乘法算子和微分算子。它们是Hilbert空间
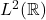 上的自伴算子
上的自伴算子![Rendered by QuickLaTeX.com \[ Xf(x) = xf(x),\; Pf(x) = \frac{1}{2\pi i}f'(x). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e27c24b4c5fbd8a508b898869f88d6e5_l3.png)
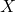 、
、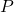 的Poisson括号为
的Poisson括号为![Rendered by QuickLaTeX.com \[ [X, P]f = \frac{1}{2\pi i}[xf' - (xf)'] = -\frac{1}{2\pi i}f. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e5bf3a4c7704ee00b5fd55e9e1f73caa_l3.png)
- 由上面的笔记可知,
对![Rendered by QuickLaTeX.com \[ \frac{1}{4\pi}||f||_2^2 = \frac 12|\langle{[X, P]f, f}\rangle_{L^2}| \leq ||(X - a)f||_2 \cdot ||(P - b)f||_2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4367aff8bfd5425e390e1d3aafe389da_l3.png)
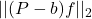 使用Plancherel定理,可得
使用Plancherel定理,可得![Rendered by QuickLaTeX.com \[ \frac{1}{4\pi}||f||_2^2 \leq ||(x - a)f||_2 \cdot ||(\xi - b)\widehat{f}||_2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f11d82a0f6bfe63c3094b308ab66e975_l3.png)
- 在时频分析中,测不准原理为
![Rendered by QuickLaTeX.com \[ \frac{1}{4\pi}||x||_2^2 \leq ||(t - t_0)x(t)||_2 \cdot ||(f - f_0)\widehat{x}(f)||_2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ba7164fce080cd986a27c4d14896d385_l3.png)
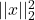 是信号的能量,
是信号的能量,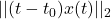 、
、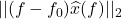 分别表示信号在时间
分别表示信号在时间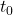 、频率
、频率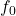 附近的集中程度
附近的集中程度- 如果我们测量一定能量的信号,那么它越集中于任何时间
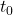 ,就越偏离于任何频率
,就越偏离于任何频率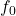 。因此,我们无法测量出信号的瞬时频率。这与测量仪器的精度无关,而是由数学本质决定的
。因此,我们无法测量出信号的瞬时频率。这与测量仪器的精度无关,而是由数学本质决定的
量子力学中的Heisenberg测不准原理
- 我们使用量子化的物质波中的Fourier变换。由此可知
- 位置
 经过Fourier变换后变为
经过Fourier变换后变为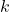 ,并且动量
,并且动量 ,所以我们可以得到位置
,所以我们可以得到位置 、动量
、动量 的Heisenberg测不准原理
的Heisenberg测不准原理 - 当波函数
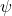 接近于粒子时,
接近于粒子时,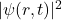 保持不变,所以我们可以认为
保持不变,所以我们可以认为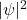 对应于粒子的概率密度函数
对应于粒子的概率密度函数
- 位置
- 考虑如下的乘法算子和微分算子。它们是Hilbert空间
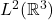 上的自伴算子
上的自伴算子![Rendered by QuickLaTeX.com \[ X_i\psi(r) = x_i\psi(r),\; P_j\psi(r) = \frac 1i\frac{\partial \psi}{\partial x_j}(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-636dde5fb7c59a58374d6103f7394186_l3.png)
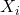 、
、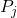 的Poisson括号为
的Poisson括号为![Rendered by QuickLaTeX.com \[ [X_i, P_j]\psi = \frac 1i[x_i\partial_j\psi - \partial_j(x_i\psi)] = -\frac 1i\psi\delta_{ij}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-70edcf3a77bb6db2cf293fbaa6e96f0b_l3.png)
- 由上面的笔记可知,
对![Rendered by QuickLaTeX.com \[ \frac 12||\psi||_2^2\delta_{ij} = \frac 12|\langle{[X_i, P_j]\psi, \psi}\rangle_{L^2}| \leq ||(X_i - a)\psi||_2 \cdot ||(P_j - b)\psi||_2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fd4e6e389a7edc6d1a8ea54605ac681d_l3.png)
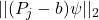 使用Plancherel定理,可得
使用Plancherel定理,可得![Rendered by QuickLaTeX.com \[ \frac 12||\psi||_2^2\delta_{ij} \leq ||(x_i - a)\psi(r)||_2 \cdot ||(k_j - b)\widehat{\psi}(k)||_2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c4ece3943bf4e7307d9ccaca930293dd_l3.png)
- 对于概率密度函数
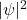 ,我们有
,我们有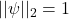 ,并且
,并且
- 位置的数学期望为
位置的方差为![Rendered by QuickLaTeX.com \[ \mathbb{E}[x_i] = \int_{\mathbb{R}^3} x_i|\psi(r)|^2dr. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2e367ae05ace4dfa21a9abfee759933e_l3.png)
![Rendered by QuickLaTeX.com \[ (\Delta x_i)^2 = \int_{\mathbb{R}^3} (x_i - \mathbb{E}[x_i])^2|\psi(r)|^2dr. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c37867269959d9e72b75d0c49778a54d_l3.png)
- 动量的数学期望为
动量的方差为![Rendered by QuickLaTeX.com \[ \mathbb{E}[p_j] = \int_{\mathbb{R}^3} \hbar k_j|\widehat{\psi}(k)|^2dk. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4fdbb167579a79a98edabf9caf6adc93_l3.png)
![Rendered by QuickLaTeX.com \[ (\Delta p_j)^2 = \int_{\mathbb{R}^3} (\hbar k_j - \mathbb{E}[p_j])^2|\widehat{\psi}(k)|^2dk. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-90d7e89af1404a519fd7491a0bb4c52e_l3.png)
- 位置的数学期望为
- 在量子力学中,Heisenberg测不准原理为
利用![Rendered by QuickLaTeX.com \[ \frac 12\delta_{ij} \leq ||(x_i - \mathbb{E}[x_i])\psi(r)||_2 \cdot ||(k_j - \mathbb{E}[p_j] / \hbar)\widehat{\psi}(k)||_2 = \Delta x_i \cdot \frac{1}{\hbar}\Delta p_j. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e7ce5493a5fb189ea7de1520e10adfae_l3.png)
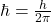 ,
,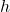 为Planck常数,当
为Planck常数,当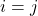 时,
时,![Rendered by QuickLaTeX.com \[ \Delta x_i \cdot \Delta p_i \geq \frac{h}{4\pi}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8aae49af5332436a457630fb0d3333ef_l3.png)
- 在Lagrange力学中,根据Newton方程,给定初始位置、初始速度,我们可以求解任意时刻的位置、速度。然而,在量子力学中,我们无法同时测量出任意时刻的位置、速度。这与测量仪器的精度无关,而是由数学本质决定的