参考资料:The Lambda Calculus Its Syntax and Semantics
Lambda项
- 关于归纳定义,可参见从不动点定理到编程语言
- Lambda演算是函数的演算
- 函数
 –> 抽象
–> 抽象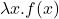
- 求值
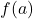 –> 应用
–> 应用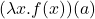
- 函数的变量可以重命名,
![Rendered by QuickLaTeX.com \[ f \rightarrow \lambda x.f(x),\; \lambda y.f(y). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-317dba11b9338985329a0e2bee408c10_l3.png)
- 函数的求值可以视为替换,
![Rendered by QuickLaTeX.com \[ f(a) \rightarrow (\lambda x.f(x))(a) = f(x)|_{x = a}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a97728aeeffb7934bf17833a9ad3426c_l3.png)
- 在不同的地方,
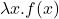 有不同的形式。在数学中,它可以记为
有不同的形式。在数学中,它可以记为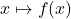 ;在编程语言中,它可以记为fn x => f(x)
;在编程语言中,它可以记为fn x => f(x)
- 函数
- 上面的演算经过形式化,可以得到无类型的Lambda演算,它可能不符合函数的特点。比如,函数应该应用于变量,但是我们允许变量应用于变量
- (变量)变量的集合
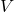
- (抽象)变量
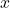 ,表达式
,表达式 –>
–> 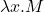
- (应用)表达式
 、
、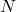 –>
–> 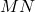
- (变量)变量的集合
- Lambda项
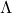 ,归纳定义
,归纳定义
- (变量)如果
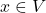 ,那么
,那么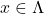
- (抽象)如果
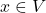 ,
, ,那么
,那么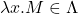
- (应用)如果
 、
、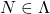 ,那么
,那么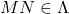
- (变量)如果
 的子项
的子项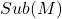 ,归纳定义
,归纳定义
- (变量)
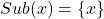
- (抽象)
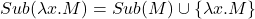
- (应用)
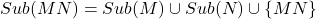
- (变量)
 的自由变量
的自由变量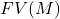 ,归纳定义
,归纳定义
- (变量)
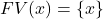
- (抽象)
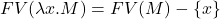
- (应用)
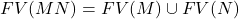
- 也就是说,出现在
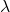 后面的变量是绑定变量,不出现在
后面的变量是绑定变量,不出现在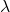 后面的变量是自由变量。如果
后面的变量是自由变量。如果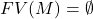 ,即
,即 没有自由变量,那么
没有自由变量,那么 称为闭的Lambda项
称为闭的Lambda项
- (变量)
替换、Alpha转换、Beta化归
- 在Lambda项
 中,将其中的变量
中,将其中的变量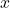 替换为另一个Lambda项
替换为另一个Lambda项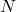 ,记为
,记为
替换的规则,归纳定义![Rendered by QuickLaTeX.com \[ M[x \mapsto N] \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-57379df80c800e14dc8b2a34c02218df_l3.png)
- (变量)
![Rendered by QuickLaTeX.com x[x \mapsto N] \equiv N](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-80a0e9c2fbe15a0817ffbd72aa4aae34_l3.png) ,
,![Rendered by QuickLaTeX.com y[x \mapsto N] \equiv y](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-167f25509c9f843d8a7d8c35646e99cf_l3.png) (
(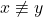 )
) - (抽象)
![Rendered by QuickLaTeX.com (\lambda y.M)[x \mapsto N] \equiv \lambda y.(M[x \mapsto N])](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f5e6daae9f3903b2e198b40a903f8acc_l3.png)
- (应用)
![Rendered by QuickLaTeX.com (M_1M_2)[x \mapsto N] \equiv (M_1[x \mapsto N])(M_2[x \mapsto N])](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e9ddd19efb7c82e37ea94ed362074592_l3.png)
- (变量)
- (Alpha转换)将函数的变量
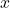 重命名为变量
重命名为变量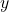 ,这对应于Alpha转换(Alpha Conversion)
,这对应于Alpha转换(Alpha Conversion)
我们需要避免如下的情形,比如![Rendered by QuickLaTeX.com \[ \lambda x.M \equiv_\alpha \lambda y.M[x \mapsto y]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2bde277d9bf007ab4386d93c9c4942fb_l3.png)
- (新的绑定旧的)
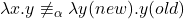
- (旧的绑定新的)
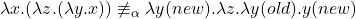
- 也就是说,重名名使用的变量
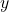 不能是
不能是 的自由变量,也不能是
的自由变量,也不能是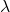 后面的绑定变量,所以我们必须使用全新的变量,比如
后面的绑定变量,所以我们必须使用全新的变量,比如![Rendered by QuickLaTeX.com \[ \lambda x.y \equiv_\alpha \lambda z.y,\; \lambda x.(\lambda z.(\lambda y.x)) \equiv_\alpha \lambda w.\lambda z.\lambda y.w \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1fe3f93af6fd9cca31629ddd8610c20d_l3.png)
- 因为
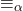 是一个等价关系,所以也叫做Alpha等价。以后,我们将Alpha等价的Lambda项视为恒等的,并且将
是一个等价关系,所以也叫做Alpha等价。以后,我们将Alpha等价的Lambda项视为恒等的,并且将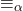 视为
视为
- (新的绑定旧的)
- (Beta化归)将函数的求值视为替换,这对应于Beta化归(Beta Reduction)
除了Beta化归以外,我们还有如下的关系![Rendered by QuickLaTeX.com \[ (\lambda x.M)(N) = M[x \mapsto N]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a54dd838a256a6c59978b548cf58f7e0_l3.png)
- (等价关系)
 是一个等价关系
是一个等价关系 - (抽象)如果
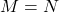 ,那么
,那么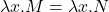
- (应用)如果
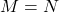 ,那么
,那么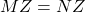 ,
,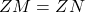
- (等价关系)
Church-Rosser定理
- 根据Beta化归,我们可以对Lambda项进行计算,这类似于函数的化简
- 然而,Lambda项的计算可能没有结果,或者结果不唯一。Church-Rosser定理用于刻画Lambda项的计算结果