参考资料:常微分方程教程
Bessel方程
- Bessel方程为如下二阶ODE。在平面波、球面波、柱面波中,它对应于球面波的径向方向
利用幂级数解法,令![Rendered by QuickLaTeX.com \[ x^2\frac{d^2y}{dx^2} + x\frac{dy}{dx} + (x^2 - \alpha^2)y = 0,\; \alpha \geq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-df3c365b85bc31582320556b54bf1d99_l3.png)
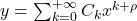 ,
,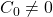 。那么,
。那么,
其中,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} 0 &= x^2\sum_{k = 0}^{+\infty} C_k(k + \rho)(k + \rho - 1)x^{k + \rho - 2} + x\sum_{k = 0}^{+\infty} C_k(k + \rho)x^{k + \rho - 1} \\ &\mathrel{\phantom{=}} + (x^2 - \alpha^2)\sum_{k = 0}^{+\infty} C_kx^{k + \rho} \\ &= \sum_{k = 0}^{+\infty} C_k[(k + \rho)^2 - \alpha^2]x^{k + \rho} + \sum_{k = 0}^{+\infty} C_kx^{k + \rho + 2} \\ &= \sum_{k = 0}^{+\infty} [C_k(k + \rho - \alpha)(k + \rho + \alpha) + C_{k - 2}]x^{k + \rho}, \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-61cbf23bd674e971f5f94957e09738b3_l3.png)
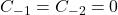 。对于
。对于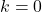 ,
,![Rendered by QuickLaTeX.com \[ C_0(\rho - \alpha)(\rho + \alpha) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1df776e2776728a6d8835a28f83c2abf_l3.png)
Bessel函数
- 第一种情形,
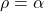
- 我们有递推公式
![Rendered by QuickLaTeX.com \[ C_kk(2\alpha + k) + C_{k - 2} = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c2cb6035bc6ea419ac294df320e20504_l3.png)
- 我们有
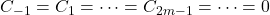 ,并且
,并且
如果取![Rendered by QuickLaTeX.com \[ C_{2m} = \prod_{l = 1}^m \frac{-1}{2l(2\alpha + 2l)}C_0 = \frac{(-1)^m}{2^{2m}m!\prod_{l = 1}^m(\alpha + l)}C_0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e2276c35f3b692f2fa8baee37e6300a2_l3.png)
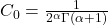 ,那么我们可以得到解
,那么我们可以得到解![Rendered by QuickLaTeX.com \[ y = J_\alpha(x) = \sum_{m = 0}^\infty \frac{(-1)^m}{\Gamma(m + 1)\Gamma(\alpha + m + 1)}\bigg(\frac{x}{2}\bigg)^{2m + \alpha}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7df664d21b07ef06f45ceb23deac1611_l3.png)
- 我们有递推公式
- 第二种情形,
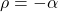
- 我们有递推公式
![Rendered by QuickLaTeX.com \[ C_k(k - 2\alpha)k + C_{k - 2} = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-867f611cb0538eb1f84643db2bc5cdae_l3.png)
- 如果
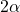 不是整数,那么我们有
不是整数,那么我们有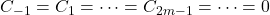 ,并且
,并且
如果取![Rendered by QuickLaTeX.com \[ C_{2m} = \prod_{l = 1}^m \frac{-1}{(2l - 2\alpha)2l}C_0 = \frac{(-1)^m}{2^{2m}m!\prod_{l = 1}^m(l - \alpha)}C_0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-378b585289376b226cead5d65f5da544_l3.png)
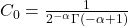 ,那么我们可以得到解
,那么我们可以得到解![Rendered by QuickLaTeX.com \[ y = J_{-\alpha}(x) = \sum_{m = 0}^\infty \frac{(-1)^m}{\Gamma(m + 1)\Gamma(-\alpha + m + 1)}\bigg(\frac{x}{2}\bigg)^{2m - \alpha}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2b61b6a6c343f76b9c2052d94e1cabc7_l3.png)
- 如果
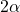 是奇数
是奇数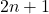 ,那么
,那么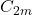 和上面一样,并且
和上面一样,并且
递推公式在![Rendered by QuickLaTeX.com \[ C_{-1} = C_1 = \cdots = C_{2n - 1} = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-51a4ee9239042e0e0d8006136eaf5b04_l3.png)
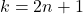 时成立。如果令
时成立。如果令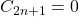 ,那么我们回到上面的情形
,那么我们回到上面的情形 - 如果
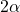 是偶数
是偶数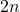 ,那么
,那么
递推公式在![Rendered by QuickLaTeX.com \[ C_0 \neq 0, \ldots, C_{2n - 2} \neq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-93b39e7edc78ecaab6df868d5d143288_l3.png)
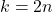 时不成立
时不成立
- 我们有递推公式
- 当
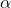 不是整数时,我们有两个线性无关的解
不是整数时,我们有两个线性无关的解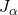 、
、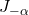 。通常,我们使用
。通常,我们使用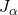 ,以及
,以及
当![Rendered by QuickLaTeX.com \[ Y_\alpha(x) = \frac{J_\alpha(x)\cos(\alpha\pi) - J_{-\alpha}(x)}{\sin(\alpha\pi)}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d8ecb10bcf6c7a102aadb91f1f1ed3ca_l3.png)
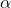 是整数
是整数 时,我们使用
时,我们使用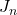 ,以及
,以及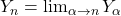
- 实际上,
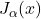 、
、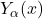 类似于
类似于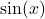 、
、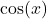 ,它们分别称为第一类、第二类Bessel函数
,它们分别称为第一类、第二类Bessel函数