参考资料:Introduction to Sonar Transducer Design
Laplace-Beltrami算子
- 对于电磁波
- 对于声波,我们考虑频谱离散的情形
然后求解齐次Helmholtz方程![Rendered by QuickLaTeX.com \[ p(\cdot, t) = \sum_a p_a(\cdot)e^{j\omega_a t}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8b5a9f0aea3a2a467f5a0362d3605026_l3.png)
我们不使用Fourier变换,而是在直角坐标系、球坐标系、柱坐标系下使用分离变量法,这更加具有几何意义![Rendered by QuickLaTeX.com \[ \Delta p_a + k^2p_a = 0,\; k = \frac{\omega_a}{c}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ff3b07ebedc60d222ebb169088fd3b2b_l3.png)
- 在局部坐标系下,Laplace算子
 可以视为Riemann流形上的Laplace-Beltrami算子
可以视为Riemann流形上的Laplace-Beltrami算子
- 直角坐标系
![Rendered by QuickLaTeX.com \[ \Delta = \partial_{xx} + \partial_{yy} + \partial_{zz}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-57444215294159e05bc8961e3557eb85_l3.png)
- 球坐标系
- 坐标变换
![Rendered by QuickLaTeX.com \[ x = r\sin\theta\cos\phi,\; y = r\sin\theta\sin\phi,\; z = r\cos\theta. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-485bff509719252254fcaf1f07d9b14a_l3.png)
- Jacobi矩阵
![Rendered by QuickLaTeX.com \[ J = \begin{bmatrix}\sin\theta\cos\phi & r\cos\theta\cos\phi & -r\sin\theta\sin\phi \\ \sin\theta\sin\phi & r\cos\theta\sin\phi & r\sin\theta\cos\phi \\ \cos\theta & -r\sin\theta & 0\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-db1650c00b4c1e6811e6cbe7e181cf1b_l3.png)
- Riemann度量
![Rendered by QuickLaTeX.com \[ g = \begin{bmatrix}1 & 0 & 0 \\ 0 & r^2 & 0 \\ 0 & 0 & r^2\sin^2\theta\end{bmatrix},\; G = \det(g) = r^4\sin^2\theta. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-23dd79eb12b9251224147ba317cc5739_l3.png)
- Laplace-Beltrami算子
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \Delta &= \frac{1}{\sqrt{G}}[\partial_r(\sqrt{G}g^{rr}\partial_r) + \partial_\theta(\sqrt{G}g^{\theta\theta}\partial_\theta) + \partial_\phi(\sqrt{G}g^{\phi\phi}\partial_\phi)] \\ &= \frac{1}{r^2\sin\theta}\bigg[\partial_r(r^2\sin\theta\partial_r) + \partial_\theta(\sin\theta\partial_\theta) + \partial_\phi\bigg(\frac{1}{\sin\theta}\partial_\phi\bigg)\bigg] \\ &= \partial_{rr} + 2r^{-1}\partial_r + r^{-2}\partial_{\theta\theta} + r^{-2}\cot\theta\partial_\theta + (r\sin\theta)^{-2}\partial_{\phi\phi}. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8d441227f9fe8341fcd94aa47936b030_l3.png)
- 坐标变换
- 柱坐标系
- 坐标变换
![Rendered by QuickLaTeX.com \[ x = r\cos\theta,\; y = r\sin\theta,\; z = z. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3305ee82c9ed1c93be98627e090d1c1f_l3.png)
- Jacobi矩阵
![Rendered by QuickLaTeX.com \[ J = \begin{bmatrix}\cos\theta & -r\sin\theta & 0 \\ \sin\theta & r\cos\theta & 0 \\ 0 & 0 & 1\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6d9e3cd79564a0c6375d761207eb2c43_l3.png)
- Riemann度量
![Rendered by QuickLaTeX.com \[ g = \begin{bmatrix}1 & 0 & 0 \\ 0 & r^2 & 0 \\ 0 & 0 & 1\end{bmatrix},\; G = \det(g) = r^2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1916680d5f91634fe7072ea93f079352_l3.png)
- Laplace-Beltrami算子
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \Delta &= \frac{1}{\sqrt{G}}[\partial_r(\sqrt{G}g^{rr}\partial_r) + \partial_\theta(\sqrt{G}g^{\theta\theta}\partial_\theta) + \partial_z(\sqrt{G}g^{zz}\partial_z)] \\ &= \frac 1r\bigg[\partial_r(r\partial_r) + \partial_\theta(r^{-1}\partial_\theta) + \partial_z(r\partial_z)\bigg] \\ &= \partial_{rr} + r^{-1}\partial_r + r^{-2}\partial_{\theta\theta} + \partial_{zz}. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-112384083936bca11f260e5f92cfe107_l3.png)
- 坐标变换
- 直角坐标系
求解齐次Helmholtz方程
- 直角坐标系——平面波
- 考虑分离变量的解
由Laplace-Beltrami算子在直角坐标系下的表达式,可得![Rendered by QuickLaTeX.com \[ p_a = X(x)Y(y)Z(z). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-92c5375f4cc5b61856fa539454b218de_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{X''}{X} + \frac{Y''}{Y} + \frac{Z''}{Z} + k^2 = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-986f0d6cbc05b23420b4f5e3e64ea624_l3.png)
- 由于方程中包含
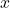 、
、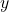 、
、 的项分别只有
的项分别只有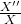 、
、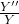 、
、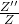 ,故我们分别令其为常数
,故我们分别令其为常数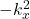 、
、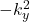 、
、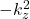 。由此可知,
。由此可知,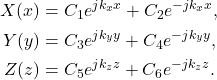
- 波动方程的解为如下平面波的线性组合
其中![Rendered by QuickLaTeX.com \[ p = e^{j[(\pm k_x)x + (\pm k_y)y + (\pm k_z)z]}e^{j\omega_at}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-96caa1f5ecf2e1f01dda013934e2e426_l3.png)
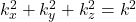
- 考虑分离变量的解
- 球坐标系——球面波
- 考虑分离变量的解
由Laplace-Beltrami算子在球坐标系下的表达式,可得![Rendered by QuickLaTeX.com \[ p_a = R(r)\Theta(\theta)\Phi(\phi). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ed1047e403135eea22d4905cb842edc4_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{R'' + 2r^{-1}R'}{R} + r^{-2}\frac{\Theta'' + \cot\theta\Theta'}{\Theta} + (r\sin\theta)^{-2}\frac{\Phi''}{\Phi} + k^2 = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0916a5e9b549076c222118def1b6a9cd_l3.png)
- 由于方程中包含
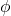 的项只有
的项只有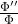 ,故我们令其为常数
,故我们令其为常数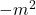 。由此可知,
。由此可知,![Rendered by QuickLaTeX.com \[ \Phi = C_1\cos(m\phi) + C_2\sin(m\phi). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-52acd477c917829ae46a44a02c385dfb_l3.png)
- 由球谐函数可知,Laplace-Beltrami算子在2维球面上的谱为
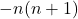 。因此,当
。因此,当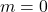 时,包含
时,包含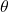 的项 –>
的项 –> 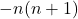 ,包含
,包含 的项 –>
的项 –> 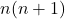
- 由球谐函数可知,Laplace-Beltrami算子在2维球面上的谱为
- 由于方程中包含
 的项只有
的项只有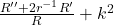 ,故我们令其在乘以
,故我们令其在乘以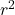 之后等于常数
之后等于常数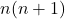 。由此可知,
。由此可知,
令![Rendered by QuickLaTeX.com \[ r^2R'' + 2rR' + [k^2r^2 - n(n + 1)]R = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2e50f60d0029774c675b7cc627ef7d70_l3.png)
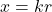 。由于
。由于![Rendered by QuickLaTeX.com \[ \frac{d}{dx} = \frac{dr}{dx}\frac{d}{dr} = \frac 1k\frac{d}{dr}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a76c75740aeb7ab0f2c9e157034c7a74_l3.png)
故![Rendered by QuickLaTeX.com \[ \frac{d^2}{dx^2} = \frac 1k\frac{d}{dr}\bigg(\frac 1k\frac{d}{dr}\bigg) = \frac{1}{k^2}\frac{d^2}{dr^2}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b1a1aaa2e1f64e028c71ffcd3896580d_l3.png)
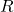 满足球面Bessel方程,
满足球面Bessel方程,
由Bessel函数可知,其解为![Rendered by QuickLaTeX.com \[ x^2\frac{d^2R}{dx^2} + 2x\frac{dR}{dx} + [x^2 - n(n + 1)]R = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-355e365834a1d0577e827728c7138cad_l3.png)
其中![Rendered by QuickLaTeX.com \[ R = C_3j_n(kr) + C_4y_n(kr), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-519151c256b238c1d1a8deee9c667e78_l3.png)
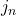 、
、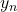 分别为第一类、第二类球面Bessel函数
分别为第一类、第二类球面Bessel函数 - 最后求解
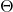 ,
,
令![Rendered by QuickLaTeX.com \[ \Theta'' + \cot\theta\Theta' + \bigg[n(n + 1) - \frac{m^2}{\sin^2\theta}\bigg]\Theta = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b51330b5de1f4adbe6f8e261c7ad7b44_l3.png)
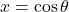 。由于
。由于![Rendered by QuickLaTeX.com \[ \frac{d}{dx} = \frac{d\theta}{dx}\frac{d}{d\theta} = \frac{1}{-\sin\theta}\frac{d}{d\theta}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7685ec447a5b6d8285c49420d260fe56_l3.png)
故![Rendered by QuickLaTeX.com \[ \frac{d^2}{dx^2} = \frac{1}{-\sin\theta}\frac{d}{d\theta}\bigg(\frac{1}{-\sin\theta}\frac{d}{d\theta}\bigg) = \frac{1}{\sin^2\theta}\frac{d^2}{d\theta^2} - \frac{\cos\theta}{\sin^3\theta}\frac{d}{d\theta}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-68e4c0d58a15ac6d479da48cb1ee01cf_l3.png)
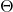 满足Legendre方程,
满足Legendre方程,
由Legendre函数可知,其解为![Rendered by QuickLaTeX.com \[ (1 - x^2)\frac{d^2\Theta}{dx^2} - 2x\frac{d\Theta}{dx} + \bigg[n(n + 1) - \frac{m^2}{1 - x^2}\bigg]\Theta = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1fc841e507a470f8d11b23e5c64cbad1_l3.png)
其中![Rendered by QuickLaTeX.com \[ \Theta = P_n^m(\cos\theta), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-481817c159d5138619c31071539dfbbe_l3.png)
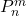 为连带Legendre函数
为连带Legendre函数 - 如果我们考虑声波向外传播,那么波动方程的解为如下球面波的线性组合
其中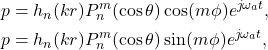
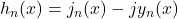 称为球面Hankel函数。在天线理论的电磁波中,我们可以得到旋转对称的解,即
称为球面Hankel函数。在天线理论的电磁波中,我们可以得到旋转对称的解,即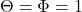 ,
,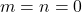 ,并且
,并且![Rendered by QuickLaTeX.com \[ R(r) = j_0(kr) - jy_0(kr) = \frac{\sin(kr)}{kr} + j\frac{\cos(kr)}{kr} = j\frac{e^{-jkr}}{kr}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-59e4c3fa647068fd7b6b32172885ced3_l3.png)
- 考虑分离变量的解
- 柱坐标系——柱面波
- 考虑分离变量的解
由Laplace-Beltrami算子在柱坐标系下的表达式,可得![Rendered by QuickLaTeX.com \[ p_a = R(r)\Theta(\theta)Z(z). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b8d2dbf69ee851b5560ad314ea82a911_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{R'' + r^{-1}R'}{R} + r^{-2}\frac{\Theta''}{\Theta} + \frac{Z''}{Z} + k^2 = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-99fefa8a17285dbf42a690b6dde71202_l3.png)
- 由于方程中包含
 的项只有
的项只有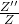 ,故我们令其为常数
,故我们令其为常数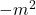 。由此可知,
。由此可知,![Rendered by QuickLaTeX.com \[ Z = C_1e^{jmz} + C_2e^{-jmz}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7b575fdaf5dd7b79e2a00c9274e7778d_l3.png)
- 由于方程中包含
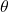 的项只有
的项只有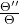 ,故我们令其为常数
,故我们令其为常数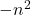 。由此可知,
。由此可知,![Rendered by QuickLaTeX.com \[ \Theta = C_3\cos(n\theta) + C_4\sin(n\theta). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f5162d372dcf5677a5d86a73c6cad0f6_l3.png)
- 最后求解
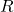 ,
,
令![Rendered by QuickLaTeX.com \[ r^2R'' + rR' + [(k^2 - m^2)r^2 - n^2]R = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-00c5b05128ade85a27caa77302c6b406_l3.png)
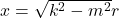 。类似于球坐标系的情形,
。类似于球坐标系的情形,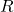 满足Bessel方程,
满足Bessel方程,
其解为![Rendered by QuickLaTeX.com \[ x^2\frac{d^2R}{dx^2} + x\frac{dR}{dx} + (x^2 - n^2)R = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-970770115d5ba33698cf076819cf7a14_l3.png)
其中![Rendered by QuickLaTeX.com \[ R = C_5J_n(\sqrt{k^2 - m^2}r) + C_6Y_n(\sqrt{k^2 - m^2}r), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5707570818e7ce1626932ca650016ec6_l3.png)
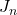 、
、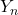 分别为第一类、第二类Bessel函数
分别为第一类、第二类Bessel函数 - 如果我们考虑声波向外传播,那么波动方程的解为如下柱面波的线性组合
其中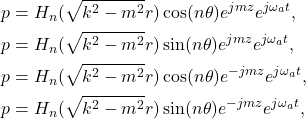
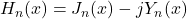 称为Hankel函数
称为Hankel函数
- 考虑分离变量的解