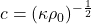参考资料:Acoustics An Introduction to Its Physical Principles and Applications
守恒定律
- 设
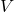 为流体中的体积(比如空气)
为流体中的体积(比如空气) - 一般地,设
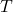 为张量。那么,
为张量。那么,
其中,![Rendered by QuickLaTeX.com \[ \frac{d}{dt}\int_V Tdx = \int_V \partial_tTdx + \int_{\partial V} Tv \cdot ndS = \int_V [\partial_tT + div(T \otimes v)]dx, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b2b6558631b1c76011566a49d27f3d50_l3.png)
 为流体的速度,并且
为流体的速度,并且![Rendered by QuickLaTeX.com \[ div(T \otimes v) = \langle{DT, v}\rangle + Tdiv(v). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-130954e991fb4b1de7e35e3f264bb741_l3.png)
- 质量守恒定律
其中,![Rendered by QuickLaTeX.com \[ 0 = \frac{d}{dt}\int_V \rho dx = \int_V [\partial_t\rho + div(\rho v)]dx, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bd4669eb35a7766c1e29d2d98e2a8b4d_l3.png)
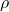 为流体的密度。由于
为流体的密度。由于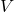 任意,故
任意,故![Rendered by QuickLaTeX.com \[ \partial_t\rho + \langle{D\rho, v}\rangle + \rho div(v) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e899b50da4de8cce3ec13507d2db6d18_l3.png)
- 动量守恒定律
其中,![Rendered by QuickLaTeX.com \[ -\int_V \nabla pdx = -\int_{\partial V} pndS = \frac{d}{dt}\int_V \rho vdx = \int_V [\partial_t(\rho v) + div(\rho v \otimes v)]dx, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b93cf99444a6cff4400d42a5d96e49ca_l3.png)
 为流体的压强。由于
为流体的压强。由于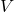 任意,故
任意,故
由质量守恒定律,上述方程等价于![Rendered by QuickLaTeX.com \[ \partial_t(\rho v) + \langle{D(\rho v), v}\rangle + \rho vdiv(v)= -\nabla p. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ccb94502751d58f8cc3b078dc0370c04_l3.png)
![Rendered by QuickLaTeX.com \[ \rho[\partial_tv + \langle{Dv, v}\rangle] = -\nabla p. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-42f888ee3190edc39ad56d0aaa175bff_l3.png)
线性声学的假设
- 为了得到线性声学的方程,我们需要做如下假设
- 我们只考虑
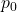 、
、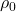 处的线性扰动
处的线性扰动
所以方程只保留线性、一阶项![Rendered by QuickLaTeX.com \[ p' = p_0 + p,\; \rho' = \rho_0 + \rho, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b39c554f4270f7cb761baff1b8f388ef_l3.png)
- 流体在空间上是均匀的(homogeneous),在时间上是静止的(quiescent),所以
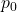 、
、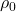 与空间、时间无关
与空间、时间无关
- 我们只考虑
- 由上面的方程,
![Rendered by QuickLaTeX.com \[ \partial_t(\rho_0 + \rho) + \langle{D(\rho_0 + \rho), v}\rangle + (\rho_0 + \rho)div(v) = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0b976dbb34c42a352d831ed316834b19_l3.png)
如果方程只保留线性、一阶项,那么可得线性声学的方程![Rendered by QuickLaTeX.com \[ (\rho_0 + \rho)[\partial_tv + \langle{Dv, v}\rangle] = -\nabla(p_0 + p). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c98ab5735c23c46a15e8eb6d0b0df165_l3.png)
![Rendered by QuickLaTeX.com \[ \partial_t\rho + \rho_0div(v) = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-10d708a991a828b3cf152d6c8e17460e_l3.png)
![Rendered by QuickLaTeX.com \[ \rho_0\partial_tv = -\nabla p. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e58a30f4e997b97f14fb14c82bcbb519_l3.png)
- 如果流体是可压缩的,等温压缩率为
那么,![Rendered by QuickLaTeX.com \[ \kappa = \frac 1\rho\frac{\partial\rho}{\partial p}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-886a296f09ed496fa85f85eb5887696b_l3.png)
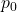 、
、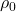 处的线性扰动满足
处的线性扰动满足
从而,![Rendered by QuickLaTeX.com \[ \rho = \frac{\partial\rho}{\partial p}(p_0)p = \kappa\rho_0p. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-21dfc13e3d4cdf879fa88ced22c7a0e6_l3.png)
这是波动方程。因此,声音可以通过声波的形式传播,传播速度为![Rendered by QuickLaTeX.com \[ \kappa\rho_0\partial_{tt}p = \partial_{tt}\rho = -div(\rho_0\partial_tv) = \Delta p, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f9e4ef87e82a71f877a1a250ba6b3f76_l3.png)