参考资料:常微分方程教程
Legendre方程
- Legendre方程为如下二阶ODE。在平面波、球面波、柱面波中,它对应于球面波的纬度方向
利用幂级数解法,令![Rendered by QuickLaTeX.com \[ (1 - x^2)\frac{d^2y}{dx^2} - 2x\frac{dy}{dx} + n(n + 1)y = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a262b2e673ff204d3fa4fde4e8e764ea_l3.png)
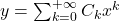 。那么,
。那么,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} 0 &= (1 - x^2)\sum_{k = 2}^{+\infty} C_kk(k - 1)x^{k - 2} - 2x\sum_{k = 1}^{+\infty} C_kkx^{k - 1} + n(n + 1)\sum_{k = 0}^{+\infty} C_kx^k \\ &= \sum_{k = 0}^{+\infty} [C_{k + 2}(k + 2)(k + 1) - C_kk(k - 1) - 2C_kk + n(n + 1)C_k]x^k \\ &= \sum_{k = 0}^{+\infty} [C_{k + 2}(k + 2)(k + 1) + C_k(n - k)(n + k + 1)]x^k. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4f0735093a1185ce2ee57d41bf43da49_l3.png)
- 因此,我们可以得到递推公式,
由此可知,![Rendered by QuickLaTeX.com \[ C_{k + 2} = -\frac{(n - k)(n + k + 1)}{(k + 2)(k + 1)}C_k. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-355068160661aa60248d471056f48396_l3.png)
当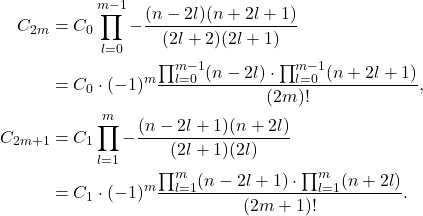
 为偶数时,只有有限个
为偶数时,只有有限个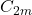 非零;当
非零;当 为奇数时,只有有限个
为奇数时,只有有限个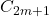 非零。在两种情形下,我们都可以得到多项式的解
非零。在两种情形下,我们都可以得到多项式的解
Legendre函数
- 下面,我们需要使用双阶乘的公式。对于
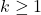 ,
,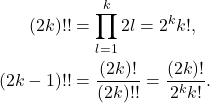
- 当
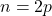 时,我们可以得到多项式的解
时,我们可以得到多项式的解
计算![Rendered by QuickLaTeX.com \[ y = C_0\sum_{m = 0}^p (-1)^m\frac{\prod_{l = 0}^{m - 1} (2p - 2l) \cdot \prod_{l = 0}^{m - 1} (2p + 2l + 1)}{(2m)!}x^{2m}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c5d97635d3131130bbb969aa727311f8_l3.png)
因此,在相差一个关于![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} &\mathrel{\phantom{=}} \prod_{l = 0}^{m - 1} (2p - 2l)\prod_{l = 0}^{m - 1} (2p + 2l + 1) \\ &= \frac{(2p)!!}{(2p - 2m)!!}\frac{(2p + 2m - 1)!!}{(2p - 1)!!} \\ &= \frac{2^pp!}{2^{p - m}(p - m)!}\frac{(2p + 2m)!/[2^{p + m}(p + m)!]}{(2p)!/(2^pp!)} \\ &= \frac{p!(2p + 2m)!p!}{(p - m)!(2p)!(p + m)!}. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8f7e90980fdbc64a633b97fcae2628b4_l3.png)
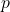 的常数下,我们可以得到Legendre函数
的常数下,我们可以得到Legendre函数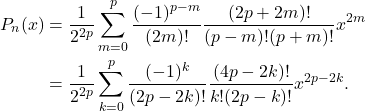
- 当
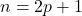 时,我们可以得到多项式的解
时,我们可以得到多项式的解
类似地,我们可以得到Legendre函数![Rendered by QuickLaTeX.com \[ y = C_1\sum_{m = 0}^p (-1)^m\frac{\prod_{l = 1}^m (2p - 2l + 2) \cdot \prod_{l = 1}^m (2p + 2l + 1)}{(2m + 1)!}x^{2m + 1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8ddb431c1a6b487d84e4a674736a38da_l3.png)
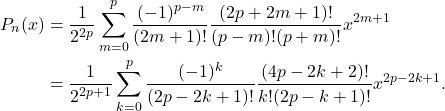
- 因为Legendre函数为多项式,所以它也叫做Legendre多项式。在两种情形下,我们都可以得到如下的表达式
![Rendered by QuickLaTeX.com \[ P_n(x) = \frac{1}{2^n}\sum_{k = 0}^{[\frac n2]} \frac{(-1)^k(2n - 2k)!}{(n - 2k)!k!(n - k)!}x^{n - 2k}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ee4ed16ffbf6d9aff9220be1a5cfcf31_l3.png)
- 因为Legendre函数的系数和二项式系数类似,所以我们也可以得到如下的Rodrigues公式
即![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \frac{d^n}{dx^n}(x^2 - 1)^n &= \frac{d^n}{dx^n}\sum_{k = 0}^n \binom{n}{k}x^{2n - 2k}(-1)^{k} \\ &= \sum_{k = 0}^{[\frac n2]}\frac{d^n}{dx^n} \binom{n}{k}x^{2n - 2k}(-1)^{k} \\ &= \sum_{k = 0}^{[\frac n2]} (-1)^{k}\frac{n!}{k!(n - k)!}\frac{(2n - 2k)!}{(n - 2k)!}x^{n - 2k} \\ &= 2^nn!P_n(x). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4e2c024ea496908dbc5d2306c6b39b37_l3.png)
![Rendered by QuickLaTeX.com \[ P_n(x) = \frac{1}{2^nn!} \frac{d^n}{dx^n}(x^2 - 1)^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e1880d90c8c38167576df7998e9f3cf1_l3.png)