静电学
- 设
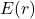 为静电场。由Coulomb定律,
为静电场。由Coulomb定律,
其中,![Rendered by QuickLaTeX.com \[ dE(r) = \frac{\rho(r')(r - r')}{|r - r'|^3}dV', \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fb8bbcd040c6f9f985ef1f63a0cac2db_l3.png)
 为电荷密度。由线性叠加原理,
为电荷密度。由线性叠加原理,
令![Rendered by QuickLaTeX.com \[ E(r) = \int \frac{\rho(r')(r - r')}{|r - r'|^3}dV'. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d1ccd0af0954ee00688ff8c49642dcc3_l3.png)
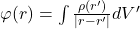 为电势。那么,
为电势。那么,![Rendered by QuickLaTeX.com \[ E(r) = -\nabla\varphi(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cb39a323ee3e5e9d2bb1bdb9c51b3e32_l3.png)
- 静电学的方程
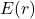 的旋度(curl)为
的旋度(curl)为![Rendered by QuickLaTeX.com \[ curlE(r) = -curl\nabla\varphi(r) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f7ca9842dc90b0062c8fb3ea640f0a4c_l3.png)
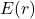 的散度(div)为
的散度(div)为
注意到![Rendered by QuickLaTeX.com \[ divE(r) = -div\nabla\varphi(r) = -\Delta\varphi(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c5c8c81e186a69aa667c3095d70ac6a0_l3.png)
因此,![Rendered by QuickLaTeX.com \[ \Delta\varphi(r) = \int \rho(r') \cdot [-4\pi\delta(r - r')]dV' = -4\pi\rho(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-42f794f9f7ddb607a070f6ebf734d4e7_l3.png)
![Rendered by QuickLaTeX.com \[ divE(r) = 4\pi\rho(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6af6b67e392efea0337da70ad0fa6234_l3.png)
静磁学
- 设
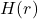 为静磁场。由Biot-Savart定律,
为静磁场。由Biot-Savart定律,
其中,![Rendered by QuickLaTeX.com \[ dH(r) = \frac 1c\frac{j(r') \times (r - r')}{|r - r'|^3}dV', \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d4108fb15b789bbcf6d7edad080197a1_l3.png)
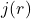 为电流密度,
为电流密度, 为光速。由线性叠加原理,
为光速。由线性叠加原理,
令![Rendered by QuickLaTeX.com \[ H(r) = \int \frac 1c\frac{j(r') \times (r - r')}{|r - r'|^3}dV'. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f62800270f175c086964fd54bc68b478_l3.png)
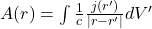 为磁势。那么,
为磁势。那么,![Rendered by QuickLaTeX.com \[ H(r) = curlA(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6bed669e29381e2a895660866171846e_l3.png)
- 由电荷守恒定律(与时间无关),
因为积分区域任意,所以![Rendered by QuickLaTeX.com \[ 0 = \int j(r) \cdot dS = \int divj(r)dV. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7b977164669f830b3890848ac4957d25_l3.png)
![Rendered by QuickLaTeX.com \[ divj(r) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2e9774598fd04741ec21b73012bd6fbf_l3.png)
- 静磁学的方程
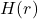 的散度(div)为
的散度(div)为![Rendered by QuickLaTeX.com \[ divH(r) = div\,curlA(r) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8eaf50211f2d19b26c9fd3b076647b9a_l3.png)
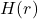 的旋度(curl)为
的旋度(curl)为
注意到![Rendered by QuickLaTeX.com \[ curlH(r) = curl\,curlA(r) = \nabla divA(r) - \Delta A(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3b9c762cde7d9b2c8e78b83212e0ddd7_l3.png)
以及由分部积分公式,![Rendered by QuickLaTeX.com \[ \Delta A(r) = \int \frac 1cj(r') \cdot [-4\pi\delta(r - r')]dV' = -\frac{4\pi}{c}j(r), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1165f45feedc715d60cdbb16568346ce_l3.png)
这里,我们需要假设积分区域外![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} divA(r) &= -\int \frac 1cj(r') \cdot \nabla'\frac{1}{|r - r'|}dV' \\ &= \int \frac 1cdiv'[j(r')] \cdot \frac{1}{|r - r'|}dV' \\ &= 0. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a3400db074882d35c429ae3efadbce63_l3.png)
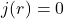 ,从而分部积分的边界项消失。因此,
,从而分部积分的边界项消失。因此,![Rendered by QuickLaTeX.com \[ curlH(r) = \frac{4\pi}{c}j(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8b54311df5c4a7317662d9b8eebf56c1_l3.png)
导出Maxwell方程组
- 设
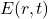 、
、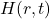 分别为与时间有关的电场、磁场
分别为与时间有关的电场、磁场 - (磁生电)由Faraday定律,
因为积分区域任意,所以![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} 0 &= \int E(r, t) \cdot dl + \frac 1c\int \frac{\partial H(r, t)}{\partial t} \cdot dS \\ &= \int \bigg[curlE(r, t) + \frac 1c\frac{\partial H(r, t)}{\partial t}\bigg] \cdot dS. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cc3851345d6c1fc956ac7ebb5ffeb3ba_l3.png)
![Rendered by QuickLaTeX.com \[ curlE(r, t) = -\frac 1c\frac{\partial H(r, t)}{\partial t}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-895a196f2a0d848016bedff82a1f0963_l3.png)
- 由电荷守恒定律(与时间有关),
因为积分区域任意,所以![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} 0 &= \int \frac{\partial\rho(r, t)}{\partial t}dV + \int j(r, t) \cdot dS \\ &= \int \bigg[\frac{\partial\rho(r, t)}{\partial t} + divj(r, t)\bigg]dV. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-660c905900e2e5e99e269141c4c8a4fe_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{\partial\rho(r, t)}{\partial t} + divj(r, t) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b737c3ccf44ecbe2839590bc30eaf35f_l3.png)
- (电生磁)注意,
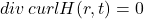 必须成立。我们令
必须成立。我们令
从而,![Rendered by QuickLaTeX.com \[ curlH(r, t) = \frac 1c\frac{\partial E(r, t)}{\partial t} + \frac{4\pi}{c}j(r, t), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-138c8f06b39430fd519f2fabf0e4f6b6_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} div\,curlH(r, t) &= \frac{4\pi}{c}\bigg[\frac{1}{4\pi}\frac{\partial divE(r, t)}{\partial t} + divj(r, t)\bigg] \\ &= \frac{4\pi}{c}\bigg[\frac{\partial\rho(r, t)}{\partial t} + divj(r, t)\bigg] \\ &= 0. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-be6322e4cb6d13228b6dcc703309a942_l3.png)
- 最终,Maxwell方程组为
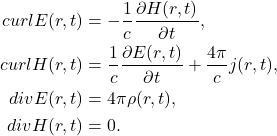
电磁波
- 如果
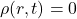 ,
,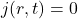 ,那么由Maxwell方程组,
,那么由Maxwell方程组,![Rendered by QuickLaTeX.com \[ \frac{1}{c^2}\frac{\partial^2E(r, t)}{\partial t^2} = -curl\,curlE(r, t) = \Delta E(r, t), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-477ab9148dbe1370fa97d20e7a76ae3c_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{1}{c^2}\frac{\partial^2H(r, t)}{\partial t^2} = -curl\,curlH(r, t) = \Delta H(r, t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b42029905a05670fc6eff0f6cfce2741_l3.png)
- 这是波动方程。因此,电磁场可以通过电磁波的形式传播,传播速度为光速