边缘算子
- 关于单纯形,可参见三角剖分和单纯复形
- 由电磁场和de Rham上同调可知
- 我们可以考虑边缘算子
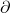 ,它应该满足
,它应该满足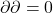
- 外积
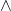 为反对称性、线性的,它对应于行列式。正如行列式的展开具有交错和的形式,外微分算子
为反对称性、线性的,它对应于行列式。正如行列式的展开具有交错和的形式,外微分算子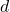 的展开也具有交错和的形式。利用伴随性,边缘算子
的展开也具有交错和的形式。利用伴随性,边缘算子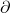 也一样
也一样
- 我们可以考虑边缘算子
- 首先,我们考虑2维情形
- 对于三角形区域
![Rendered by QuickLaTeX.com \Omega = [v_0v_1v_2]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2538aab8ec713cb925d23e5842fcb653_l3.png) ,其边界
,其边界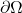 为
为
此时,边缘算子![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ {} & v_2 \ar[dl]_{-[v_0v_2]} & {} \\ v_0 \ar[rr]_{[v_0v_1]} & {} & v_1 \ar[ul]_{[v_1v_2]} } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-93bf1d0bfdbf4a3b56a15de0b3dbb8f6_l3.png)
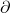 在2维区域上的展开具有交错和的形式
在2维区域上的展开具有交错和的形式![Rendered by QuickLaTeX.com \[ \partial\Omega = \sum_{i = 0}^2 (-1)^i[v_0 \cdots \widehat{v_i} \cdots v_2]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2e046bdaadfb7b3bb320e46bb390a9b5_l3.png)
- 对于一般的拓扑空间
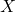 ,我们需要取
,我们需要取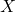 中的三角形区域
中的三角形区域
- 一种办法是取
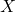 上的三角剖分(对应于单纯同调),这对
上的三角剖分(对应于单纯同调),这对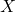 有限制
有限制 - 另一种办法是取三角形到
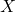 的连续映射(对应于奇异同调)。因为所有三角形都是同胚的,所以我们只需固定一个标准2-单纯形
的连续映射(对应于奇异同调)。因为所有三角形都是同胚的,所以我们只需固定一个标准2-单纯形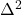 ,然后取
,然后取![Rendered by QuickLaTeX.com \[ \sigma: \Delta^2 \to X. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7b5a975488ba0fbacfddfdbfe3cd278c_l3.png)
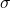 可能是退化的,像集不同胚于三角形,所以它称为奇异
可能是退化的,像集不同胚于三角形,所以它称为奇异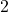 -单纯形
-单纯形
- 一种办法是取
- 对于三角形区域
- 现在,我们考虑
 维情形
维情形
- 固定一个标准
 -单纯形
-单纯形
然后取奇异![Rendered by QuickLaTeX.com \[ \Delta^n = [e_0 \cdots e_n]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a6c49344f15be82449c0cf9f4aa82b46_l3.png)
 -单纯形
-单纯形![Rendered by QuickLaTeX.com \[ \sigma: \Delta^n \to X. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0c5f31ded7ff891801f7cef577c5fa04_l3.png)
- 边缘算子
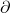 在奇异
在奇异 -单纯形
-单纯形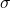 上的作用为
上的作用为
满足![Rendered by QuickLaTeX.com \[ \partial\sigma = \sum_{i = 0}^n (-1)^i\sigma|_{[e_0 \cdots \hat{e}_i \cdots e_n]}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d3a55e4046609717a2797e639f6c966a_l3.png)
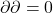 ,
,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \partial_{n - 1}\partial_n(\sigma) &= \partial_{n - 1}\bigg(\sum_{i = 0}^n (-1)^i\sigma|_{[e_0 \cdots \hat{e}_i \cdots e_n]}\bigg) \\ &= \sum_{i = 0}^n (-1)^i\sum_{j < i} (-1)^j\sigma|_{[e_0 \cdots \hat{e}_j \cdots \hat{e}_i \cdots e_n]} \\ &\quad + \sum_{i = 0}^n (-1)^i\sum_{j > i} (-1)^{j - 1}\sigma|_{[e_0 \cdots \hat{e}_i \cdots \hat{e}_j \cdots e_n]} \\ &= \sum_{i = 0}^n \sum_{j < i} [(-1)^{i + j} + (-1)^{i + j - 1}]\sigma|_{[e_0 \cdots \hat{e}_j \cdots \hat{e}_i \cdots e_n]} \\ &= 0. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cd556df9a95d122774c2d54aaf23389a_l3.png)
- 由于需要进行加法,故取奇异
 -单纯形生成的自由Abel群
-单纯形生成的自由Abel群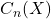 ,它称为奇异链群。同时,边缘算子
,它称为奇异链群。同时,边缘算子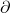 自由扩张到
自由扩张到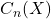 ,得到Abel群的同态,
,得到Abel群的同态,![Rendered by QuickLaTeX.com \[ \partial_n: C_n(X) \to C_{n - 1}(X). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b405f7680b5f72e58f94e4320094ce7a_l3.png)
- 固定一个标准
奇异链复形、奇异同调群
- 奇异链群、边缘算子构成Abel群、Abel群的同态形成的序列
满足![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ \cdots \ar[r] & C_n(X) \ar[r]^-{\partial_n} & C_{n - 1}(X) \ar[r] & \cdots \ar[r] & C_1(X) \ar[r]^-{\partial_1} & C_0(X) \ar[r]^-{\partial_0} & 0 }, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d32f7b1bed27aed124bac5a6f772fd1c_l3.png)
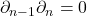 。这样的结构称为奇异链复形
。这样的结构称为奇异链复形
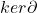 中的元素称为闭链,
中的元素称为闭链,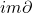 中的元素称为边缘链。因为奇异链复形满足
中的元素称为边缘链。因为奇异链复形满足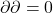 ,所以
,所以![Rendered by QuickLaTeX.com \[ im\partial_{n + 1} \subset ker\partial_n \subset C_n(X). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-84d085049662868d0bb3b14e4091daf8_l3.png)
- 奇异同调群为
边缘链一定是闭链,但是闭链不一定是边缘链,奇异同调群反映了从闭链到边缘链的障碍![Rendered by QuickLaTeX.com \[ H_n(X) = ker\partial_n/im\partial_{n + 1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-01258b6c9ecad4d4cad02b37a4c4a0cc_l3.png)
- 拓扑空间的连续映射
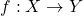 ,诱导奇异链复形的链映射
,诱导奇异链复形的链映射
满足![Rendered by QuickLaTeX.com \[ f_*: C_n(X) \to C_n(Y),\; \sigma \mapsto f \circ \sigma, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-987228ef556ccf1740bc86a33a98adec_l3.png)
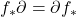 ,
,![Rendered by QuickLaTeX.com \[ f_*\partial(\sigma) = \sum_{i = 0}^n (-1)^if \circ \sigma|_{[e_0 \cdots \hat{e}_i \cdots e_n]} = \partial f_*(\sigma). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-89263d048bd2eb040d0e545e5923b3d1_l3.png)
- 链映射将闭链映射到闭链,将边缘链映射到边缘链,
![Rendered by QuickLaTeX.com \[ \partial c_n = 0 \Rightarrow \partial f_*(c_n) = f_*\partial(c_n) = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e0f7c4126c50bf65561a6f1868615791_l3.png)
![Rendered by QuickLaTeX.com \[ c_{n - 1} = \partial(c_n) \Rightarrow f_*(c_{n - 1}) = f_*\partial(c_n) = \partial f_*(c_n). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5e0f3f0150361e0fa60b54bdfcd06475_l3.png)
- 链映射
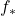 诱导奇异同调群的同态
诱导奇异同调群的同态
这里,代表元素![Rendered by QuickLaTeX.com \[ f_*: H_n(X) \to H_n(Y),\; [c_n] \mapsto [f_*(c_n)]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-795dee1c433135f421d95bc93e0fd30b_l3.png)
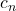 为闭链,并且边缘链
为闭链,并且边缘链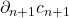 等价于0
等价于0
- 链映射将闭链映射到闭链,将边缘链映射到边缘链,
奇异同调群的长正合列
- 由从链复形到同调群可知,从链复形的短正合列,可以得到同调群的长正合列
- 关键在于构造链复形的短正合列。一种办法是使用子群、商群的分解,
因此,我们有奇异链复形的短正合列,![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ 0 \ar[r] & A \ar[r]^-{i} & A' \ar[r]^-{p} & A' / A \ar[r] & 0 } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0086346a4cc4195fcd710b2a5aea47c9_l3.png)
其中,![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ 0 \ar[r] & C_*(A) \ar[r]^-{i} & C_*(X) \ar[r]^-{p} & C_*(X) / C_*(A) \ar[r] & 0 } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3b67438ba5d0fd9f3f82e3d672c8ecb5_l3.png)
 为子空间
为子空间
- 将
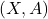 作为拓扑空间对,将
作为拓扑空间对,将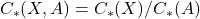 作为相对奇异链群,它对应于相对奇异同调群
作为相对奇异链群,它对应于相对奇异同调群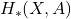 。因此,我们有奇异同调群的长正合列
。因此,我们有奇异同调群的长正合列![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ \cdots \ar[r] & H_{n + 1}(X, A) \ar[r]^-{\partial} & H_n(A) \ar[r]^-{i_*} & H_n(X) \ar[r]^-{p_*} & H_n(X, A) \ar[r] & \cdots } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-656a362cf0fe810f2fcfa403704b64f4_l3.png)
- 奇异同调群的长正合列,既可以看成由子空间的分解生成,
也可以看成由子空间、商空间的分解生成,![Rendered by QuickLaTeX.com \[ X = A \cup (X - A), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6823c804a03fe7c0d8cde50543a125a8_l3.png)
第二种视角和同伦群的长正合列一致,比如对于纤维丛![Rendered by QuickLaTeX.com \[ A \hookrightarrow X \to X / A. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ef60a9e8bafd3390d0fdc803076bb0d6_l3.png)
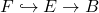 或者Lie群
或者Lie群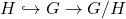 ,我们有同伦群的长正合列
,我们有同伦群的长正合列
- 将