参考资料:Measure Theory
一般的测度
- 类似于Lebesgue测度,我们可以建立一般的测度。设
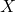 为集合
为集合
- (外测度)
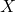 上的外测度为
上的外测度为
它满足如下条件![Rendered by QuickLaTeX.com \[ \mu^*: \mathscr{P}(X) \to [0, +\infty]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6c6e8e2e79335a47ff0142cf0f4257d9_l3.png)
- (空集)我们有
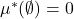
- (单调性)如果
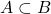 ,那么
,那么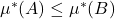
- (可数次可加性)如果
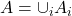 ,那么
,那么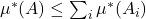
- (空集)我们有
- (
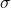 -代数)我们只考虑满足可加性的集合
-代数)我们只考虑满足可加性的集合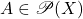 ,
,
这称为Carathéodory判别准则。满足Carathéodory判别准则的集合,称为![Rendered by QuickLaTeX.com \[ \mu^*(B) = \mu^*(A \cap B) + \mu^*(A^c \cap B) \text{ for any } B \in \mathscr{P}(X). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-47590fcc483e6407a5cbca5059a83932_l3.png)
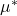 -可测集,它们构成一个子族
-可测集,它们构成一个子族
这一子族称为![Rendered by QuickLaTeX.com \[ \mathscr{M}_{\mu^*} \subset \mathscr{P}(X). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-69e5958ab17441d9b5b052809df3359c_l3.png)
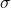 -代数,它满足如下条件
-代数,它满足如下条件
- (空集)我们有
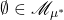
- (补集)如果
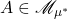 ,那么
,那么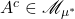
- (可数并)如果
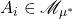 ,那么
,那么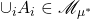
- (空集)我们有
- (测度)对于
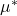 -可测集,外测度
-可测集,外测度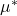 提升为测度
提升为测度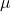 ,它满足如下条件
,它满足如下条件
- (空集)我们有
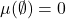
- (可数可加性)如果
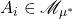 ,并且两两不相交,那么
,并且两两不相交,那么
注意,可数可加性强于单调性、可数次可加性。如果![Rendered by QuickLaTeX.com \[ \mu(\cup_i A_i) = \sum_i \mu(A_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-04e94d01bb66b8f101551ba9cc4c379a_l3.png)
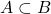 ,那么
,那么![Rendered by QuickLaTeX.com \[ \mu(A) \leq \mu(A) + \mu(B - A) = \mu(B). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-395d804cd632145b9b6a3289407170a9_l3.png)
- (空集)我们有
- (外测度)
- 测度空间是集合、集合上的
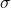 -代数、
-代数、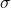 -代数上的测度构成的三元组
-代数上的测度构成的三元组![Rendered by QuickLaTeX.com \[ (X, \mathscr{A}, \mu). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-12bd575c5a3eccb3879fecb7c10b3b38_l3.png)
- 由上述可知,如果建立了
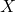 上的外测度
上的外测度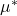 ,那么我们有测度空间
,那么我们有测度空间![Rendered by QuickLaTeX.com \[ (X, \mathscr{M}_{\mu^*}, \mu). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cb83736bb13725160664287155bcece6_l3.png)
- 对于
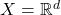 ,我们通常使用Lebesgue测度空间
,我们通常使用Lebesgue测度空间![Rendered by QuickLaTeX.com \[ (\mathbb{R}^d, \mathscr{M}_{\lambda^*}, \lambda). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c9b42d4dbac43dc18fed2fceca405293_l3.png)
- 由上述可知,如果建立了
- 如果只有集合、集合上的
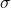 -代数,那么我们可以得到可测空间
-代数,那么我们可以得到可测空间
由于可测空间没有指定测度,故我们可以在上面建立不同的测度![Rendered by QuickLaTeX.com \[ (X, \mathscr{A}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b9119201593bfc1f77c9b5cfcf8ab921_l3.png)
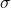 -代数是二进制、逻辑和Boole代数中的幂集代数的扩展。代数支持有限个元素的加法,
-代数是二进制、逻辑和Boole代数中的幂集代数的扩展。代数支持有限个元素的加法,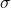 -代数支持可数个元素的加法。这里,Sigma源于可数求和
-代数支持可数个元素的加法。这里,Sigma源于可数求和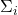
从Riemann积分到测度空间上的积分
- Lebesgue控制收敛定理、Fubini定理