范畴、函子
- 范畴的组成部分
- (对象)全体对象可能不再是一个集合,而是一个类
- (态射)类似于集合的映射
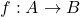
- (复合)类似于映射的复合
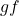 ,满足结合律
,满足结合律 - (恒等)类似于恒等映射,
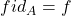 ,
,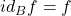
- 函子既作用于对象,也作用于态射,并且保持复合、恒等
- (对象)
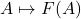
- (态射)
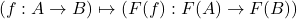
- (复合)
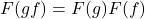
- (恒等)
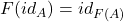
- (对象)
- 一般的范畴
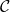 ,需要定义对象、态射,剩下的复合、恒等应该是态射的性质
,需要定义对象、态射,剩下的复合、恒等应该是态射的性质
- 对象记为
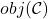
- 态射记为
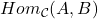 ,
, 、
、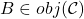
- 通常,对象不是集合,但是态射是集合,此时
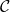 称为局部小范畴。在其他情形下,如果二者都是(或者都不是)集合,那么
称为局部小范畴。在其他情形下,如果二者都是(或者都不是)集合,那么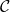 称为小范畴(或者大范畴)
称为小范畴(或者大范畴)
- 对象记为
- 如果将对象视为顶点,将态射视为有向边(箭头),那么范畴可以用有向图来描述
- 范畴通常只依赖于有向图的结构,而与对象、态射的具体内容无关。比如,有向图经过的路径,对应于态射的复合;如果两条路径的起点、终点相同,那么态射的复合相等,这构成一个交换图表
- 如果范畴
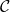 的有向图顶点不变,箭头反向,那么可以得到反范畴
的有向图顶点不变,箭头反向,那么可以得到反范畴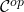 。比如,链复形范畴的反范畴为上链复形范畴
。比如,链复形范畴的反范畴为上链复形范畴 - 我们可以不断将箭头提升至高阶,比如
- (0阶)对象的箭头为态射
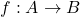 ,它对应于映射
,它对应于映射 - (1阶)态射的箭头为函子
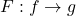 ,它对应于算子
,它对应于算子 - (2阶)函子的箭头为自然变换
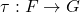 ,它对应于算子之间的变换
,它对应于算子之间的变换
- (0阶)对象的箭头为态射
- 因为有向图可以视为单纯复形,所以在高等范畴论中,我们也可以从单纯复形的视角来研究范畴
万有性质
- 集合论和范畴论
- 在集合论中,我们可以取集合的元素,然后定义新的集合
- 在范畴论中,我们只能取对象、态射,所以需要用万有性质来定义新的对象
- 范畴论和编程语言
- 在范畴论中,我们不能对元素进行操作;就像在编程语言中,我们不能对逻辑门进行操作
- 范畴论提供了一层抽象封装,使得我们可以考虑高层次结构;就像编程语言提供了一层抽象封装,使得我们可以考虑高层次算法
- 正向极限(Direct Limit)、反向极限(Inverse Limit)
- 在从不动点定理到编程语言中,我们有上确界、下确界,它们可以用万有性质来定义
- 上确界既是上界,也是最小的上界
- 对任意上界
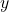 ,我们有
,我们有
- 对任意上界
- 下确界既是下界,也是最大的下界
- 对任意下界
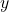 ,我们有
,我们有
- 对任意下界
- 上确界既是上界,也是最小的上界
- 因此,万有性质既要求定义的对象满足条件,也要求它具有最特殊的性质。由于后者需要用“任意对象”来叙述,故这种性质是“万有的(Universal)”
- 类似地,对任意物体,我们有Newton的万有引力定律(Newton’s Law of Universal Gravitation)
- 如果将偏序关系(
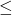 )更换为范畴中的箭头(
)更换为范畴中的箭头(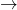 ),那么上确界可以定义为递增序列的正向极限,下确界可以定义为递减序列的反向极限
),那么上确界可以定义为递增序列的正向极限,下确界可以定义为递减序列的反向极限
- (上确界,正向极限)对任意上界
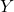 ,我们有
,我们有![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{X_1 \ar[r] & X_2 \ar[r] & \cdots \ar[r] & \underset{\longrightarrow}{\lim} X_i \ar[r] & Y.} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-81776c52c793844f6e37f19e19f32a18_l3.png)
- (下确界,反向极限)对任意下界
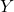 ,我们有
,我们有![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{Y \ar[r] & \underset{\longleftarrow}{\lim} X_i \ar[r] & \cdots \ar[r] & X_2 \ar[r] & X_1.} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9ece32b76705150536c67bf12de21bd3_l3.png)
- (上确界,正向极限)对任意上界
- 因为正向极限、反向极限分别对应于入射(Injection)、投射(Projection),所以它们也叫做入射极限(Injective Limit)、投射极限(Projective Limit)
- 类似地,在同调代数中,我们需要用入射消解(Injective Resolution)、投射消解(Projective Resolution)来定义导出函子
- 在从不动点定理到编程语言中,我们有上确界、下确界,它们可以用万有性质来定义
对偶
- 正向极限(入射极限)、反向极限(投射极限)是在偏序关系的图表下定义的对象,余极限(Colimit)、极限(Limit)是在一般的图表下定义的对象。因为它们的箭头是相反的,所以这一现象称为对偶(Duality)
- 正向、入射 –> 余极限
- 反向、投射 –> 极限
- 始对象(Initial Object)、终对象(Final Object)
- (余极限)对于空图表(没有对象,没有态射)
始对象定义为![Rendered by QuickLaTeX.com \[ \emptyset \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a5ae9d064266c44e0e6983f782fe87b5_l3.png)
![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ \ar[r] & Initial \ar[r] & Y } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6ee51fc0af22c21a17e552538c5434c2_l3.png)
- (极限)对于空图表(没有对象,没有态射)
终对象定义为![Rendered by QuickLaTeX.com \[ \emptyset \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a5ae9d064266c44e0e6983f782fe87b5_l3.png)
![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ Y \ar[r] & Final \ar[r] & } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d0249f67159a49fc45768bd27bfbed98_l3.png)
- (余极限)对于空图表(没有对象,没有态射)
- 余乘积(Coproduct)、乘积(Product)
- (余极限)对于离散图表(有对象,没有态射)
余乘积定义为![Rendered by QuickLaTeX.com \[ X_\alpha, \text{ for any } \alpha \in \mathscr{A} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-66ee7de3204e7756beef25f69e79107c_l3.png)
![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ X_\alpha \ar[r] & \coprod_{\alpha \in \mathscr{A}} X_\alpha \ar[r] & Y } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-96af5bda65ae45f383b921b9ec1dc22e_l3.png)
- (极限)对于离散图表(有对象,没有态射)
乘积定义为![Rendered by QuickLaTeX.com \[ X_\alpha, \text{ for any } \alpha \in \mathscr{A} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-66ee7de3204e7756beef25f69e79107c_l3.png)
![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ Y \ar[r] & \prod_{\alpha \in \mathscr{A}} X_\alpha \ar[r] & X_\alpha } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6fab8d96a53bd68e6cc311a761b42b0e_l3.png)
- (余极限)对于离散图表(有对象,没有态射)
- 推出(Pushout)、拉回(Pullback)
- (余极限)对于如下图表(有对象,有态射)
推出定义为![Rendered by QuickLaTeX.com \[ \xymatrix{ A \ar[r] \ar[d] & X_2 \\ X_1 & } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9fb9fbc9d3e0450856cc45b343ee2284_l3.png)
这里,我们省略了![Rendered by QuickLaTeX.com \[ \xymatrix{ A \ar[r] \ar[d] & X_2 \ar[d] \ar[ddr] & \\ X_1 \ar[r] \ar[drr] & X_1 \cup_A X_2 \ar[dr] & \\ & & Y } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-97891924943fac887fb1c41fbc06114b_l3.png)
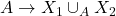 、
、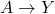 ,它们可以由交换图表中态射的复合得到
,它们可以由交换图表中态射的复合得到 - (极限)对于如下图表(有对象,有态射)
![Rendered by QuickLaTeX.com \[ \xymatrix{ & X_2 \ar[d] \\ X_1 \ar[r] & A } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d67cb233d7ea6da0e7455518204515c3_l3.png)
这里,我们省略了![Rendered by QuickLaTeX.com \[ \xymatrix{ Y \ar[drr] \ar[ddr] \ar[dr] & & \\ & X_1 \times_A X_2 \ar[r] \ar[d] & X_2 \ar[d] \\ & X_1 \ar[r] & A } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8526fd30cabfb4f7c4fc37d6e94a96e8_l3.png)
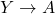 、
、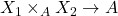 ,它们可以由交换图表中态射的复合得到
,它们可以由交换图表中态射的复合得到
- (余极限)对于如下图表(有对象,有态射)
集合论中的对象
- 在上面的定义中,名称、记号源于集合论
- 集合论和类型论
- 在集合论中,我们有不交并
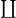 、Descartes积
、Descartes积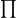
- 在类型论中,我们有并集(|)、乘积(*)
- 在集合论中,我们有不交并