Euclid几何、晶体群

变换群、几何

关于仿射变换群、射影变换群、Euclid群，可参见计算机图形学的几何变换
$\mathbb{R}^3$ 上保持定向的等距变换群为特殊Euclid群
$Isom^+(\mathbb{R}^3, g_{can}) \cong SE(3, \mathbb{R}).$
如果去掉保持定向的条件，并且考虑一般的维数 $n$ ，那么等距变换群为Euclid群
$Isom(\mathbb{R}^n, g_{can}) \cong E(n, \mathbb{R}).$
根据Erlangen纲领，几何由变换群确定
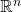- $\mathbb{R}^n$ 上的仿射几何，由仿射变换群 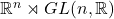$\mathbb{R}^n \rtimes GL(n, \mathbb{R})$ 确定
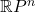- $\mathbb{R}P^n$ 上的射影几何，由射影变换群 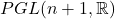$PGL(n + 1, \mathbb{R})$ 确定
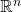- $\mathbb{R}^n$ 上的Euclid几何，由Euclid群 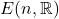$E(n, \mathbb{R})$ 确定。特别地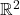， $\mathbb{R}^2$ 上的Euclid几何为平面几何， $\mathbb{R}^3$ 上的Euclid几何为立体几何
根据Erlangen纲领，几何研究变换群下的不变量。如果变换群越小，那么不变量越多、几何越丰富。因为
$E(n, \mathbb{R}) \subset \mathbb{R}^n \rtimes GL(n, \mathbb{R}) \subset PGL(n + 1, \mathbb{R}),$
所以射影几何最贫瘠、Euclid几何最丰富
- Euclid几何的不变量
  - （度量）
- 仿射几何的不变量
  - （有向Lebesgue测度比）
- 射影几何的不变量

现在，我们考虑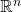上的Euclid几何
- 如果我们取离散子群 $\Gamma \subset E(n, \mathbb{R})$ ，那么我们可以得到Euclid流形
  $\mathbb{R}^n / \Gamma.$
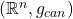  我们称 $(\mathbb{R}^n, g_{can})$ 为Euclid流形的几何模型（Geometric Model）
- 如果Euclid流形还是紧的，那么我们称 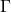$\Gamma$ 为晶体群（Crystallographic Group）。当 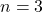$n = 3$ 时，晶体群可以刻画晶体的对称性