晶体学和几何拓扑
- 关于晶体群,可参见Euclid几何、晶体群
- 我们考虑如下晶体群
它对应的Euclid流形为3维环面![Rendered by QuickLaTeX.com \[ \Gamma = \mathbb{Z}^3, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-816612a0916444019e2e4190ad4866aa_l3.png)
![Rendered by QuickLaTeX.com \[ \mathbb{T}^3 = \mathbb{R}^3 / \mathbb{Z}^3. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-72d14b151efec00a6575c9cbb77ae7d4_l3.png)
- 在流形的三角剖分中,我们考虑将流形剖分为单纯形(Simplex),此时流形对应于一个单纯复形(Simplicial Complex)。这在2维、3维是可以实现的
- 2维流形对应于一个2维单纯复形,即多边形(Polygon),然后我们需要将多边形的边界进行粘贴
- 3维流形对应于一个3维单纯复形,即多面体(Polyhedron),然后我们需要将多面体的边界进行粘贴
- 比如,上面的3维环面
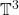 可以视为将立方体
可以视为将立方体![Rendered by QuickLaTeX.com [0, 1]^3](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-99b4b58f882484a50f7e15a13b00cc03_l3.png) 的3个相对的面进行粘贴
的3个相对的面进行粘贴
- 单纯形也可以视为胞腔(Cell),单纯复形也可以视为胞腔复形(Cell Complex)或者CW复形。在晶体学中,我们将胞腔称为单位晶胞(Unit Cell)。由上述可知,单位晶胞相当于将多面体的边界进行粘贴
- Poincaré曾经猜想,3维同调球(即同调群同构于
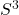 的3维闭流形)同胚于
的3维闭流形)同胚于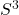 ,然而他找到了一个反例——Poincaré同调球,它相当于一个正12面体的边界进行粘贴,它是3维同调球,然而它的基本群的阶为120
,然而他找到了一个反例——Poincaré同调球,它相当于一个正12面体的边界进行粘贴,它是3维同调球,然而它的基本群的阶为120 - 据此,Poincaré提出疑问,基本群为0的3维闭流形是否同胚于
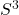 ?这称为Poincaré猜想。进一步,广义Poincaré猜想为
?这称为Poincaré猜想。进一步,广义Poincaré猜想为 维同伦球(即同伦群同构于
维同伦球(即同伦群同构于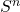 的
的 维闭流形)同胚于
维闭流形)同胚于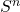
- 在化学中,我们也有多边形、多面体的结构,比如苯环(Benzene Ring)
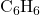 为正6边形,最小的富勒烯(Fullerene)
为正6边形,最小的富勒烯(Fullerene)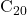 为正12面体
为正12面体
- Poincaré曾经猜想,3维同调球(即同调群同构于