参考资料:Measure Theory
公理化的层次
- 数学的历史
- (算术化)Newton、Leibniz建立了微积分的基本原理。然而,无穷小微分存在矛盾之处。微积分的算术化利用极限,将无穷小微分化归为有限差分,所以二者的演算是类似的。关于算术化,可参见从切空间到局部
- (公理化)有限差分建立在实数的加法、减法、乘法、除法之上,极限建立在实数的全序关系之上。实数的公理化将实数作为一个集合,它是一个完备的全序域。然而,Russell悖论指出,集合的构造本身存在矛盾之处,所以我们需要公理化集合论。关于公理化,可参见公理化集合论
- (结构化)我们希望将数学建立在公理化集合论的基础之上。然而,Gödel不完备定理指出,在算术的公理系统中,某些命题的真假是不可证明的。因此,我们从公理转向更广泛的结构,从集合转向更广泛的范畴。关于结构化,可参见范畴的定义
- (形式化)现在,我们可以将数学形式化,然后将其建立在计算机的计算之上。形式化通常使用类型论,它源于Russell。关于形式化,可参见数学基础——从集合论、范畴论到同伦类型论
- 在这里,我们位于公理化的层次。在集合上,我们可以建立度量、拓扑、测度
从Newton-Leibniz公式出发
- 我们从Newton-Leibniz公式出发
然后考虑这一公式的成立条件![Rendered by QuickLaTeX.com \[ f(b) - f(a) = \int_a^b f'(x)dx, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ee22e13ef084bb3934ca8e273311a321_l3.png)
- 如果
 在
在![Rendered by QuickLaTeX.com [a, b]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3a803190c367e33f6d04b9a3bf8ba342_l3.png) 上连续,在
上连续,在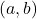 上可微,那么由Lagrange微分中值定理,
上可微,那么由Lagrange微分中值定理,
关于![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} f(b) - f(a) = \sum_i [f(x_i) - f(x_{i - 1})] = \sum_i f'(\xi_i)(x_i - x_{i - 1}). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-80354af7370609aab7f0035eb3b53bd8_l3.png)
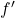 的求和为Riemann和,如果它收敛,那么求和的极限为Riemann积分,此时,Newton-Leibniz公式成立
的求和为Riemann和,如果它收敛,那么求和的极限为Riemann积分,此时,Newton-Leibniz公式成立 - 如果
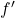 无界,那么Riemann和可以趋近于无穷。因此,我们需要
无界,那么Riemann和可以趋近于无穷。因此,我们需要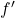 有界,此时
有界,此时
其中,![Rendered by QuickLaTeX.com \[ \sum_i m_i(x_i - x_{i - 1}) \leq \sum_i f'(\xi_i)(x_i - x_{i - 1}) \leq \sum_i M_i(x_i - x_{i - 1}), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-85160564072a9881d41e70c61052ff1d_l3.png)
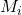 、
、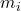 分别为
分别为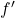 在区间
在区间![Rendered by QuickLaTeX.com [x_{i - 1}, x_i]}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d79921fae5f60eaaac67a697ef672633_l3.png) 的上、下确界。进一步,如果不等式两边收敛到同一个值,那么Riemann和也收敛到该值。因此,我们还需要
的上、下确界。进一步,如果不等式两边收敛到同一个值,那么Riemann和也收敛到该值。因此,我们还需要![Rendered by QuickLaTeX.com \[ \sum_i \omega_i(x_i - x_{i - 1}) \to 0, \text{ where } \omega_i = M_i - m_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9dab18c27ba847458c995b118c7f896e_l3.png)
- 如果
- (振幅)
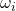 为区间
为区间![Rendered by QuickLaTeX.com [x_{i - 1}, x_i]}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d79921fae5f60eaaac67a697ef672633_l3.png) 上
上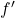 的振幅。它可以扩展为幂集上的函数,
的振幅。它可以扩展为幂集上的函数,
它具有如下性质![Rendered by QuickLaTeX.com \[ \omega: \mathscr{P}([a, b]) \to [0, +\infty],\; \omega(A) = sup_A f' - inf_Af'. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-95d9c9f2c67aa02999f1675004dc1fb8_l3.png)
- (空集)我们有
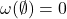
- (子集)如果
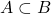 ,那么
,那么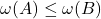
- (可数并)如果
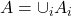 ,那么
,那么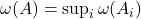
- (空集)我们有
- (长度)
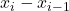 为区间
为区间![Rendered by QuickLaTeX.com [x_{i - 1}, x_i]}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d79921fae5f60eaaac67a697ef672633_l3.png) 的长度。为了将其扩展为幂集上的函数,我们用开区间
的长度。为了将其扩展为幂集上的函数,我们用开区间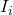 来覆盖集合,然后取总长度的下确界,
来覆盖集合,然后取总长度的下确界,
它具有如下性质![Rendered by QuickLaTeX.com \[ \lambda^*: \mathscr{P}([a, b]) \to [0, +\infty],\; \lambda^*(A) = \inf_{A \subset \cup_i I_i} \sum_i Len(I_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1e0802949e989b593af677d1a669a133_l3.png)
- (空集)我们有
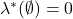
- (子集)如果
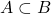 ,那么
,那么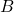 的开区间覆盖
的开区间覆盖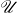 ,也是
,也是 的开区间覆盖。因此,
的开区间覆盖。因此,
对所有![Rendered by QuickLaTeX.com \[ \lambda^*(A) \leq Total\_Len(\mathscr{U}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ffe8acf77c9a93282ec5af1e6598ede9_l3.png)
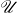 取下确界,可得
取下确界,可得![Rendered by QuickLaTeX.com \[ \lambda^*(A) \leq \lambda^*(B). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9297d1762935282561d2d5260be5aa6b_l3.png)
- (可数并)如果
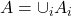 ,那么
,那么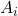 的开区间覆盖
的开区间覆盖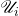 ,可以合成为
,可以合成为 的开区间覆盖。因此,
的开区间覆盖。因此,
对所有![Rendered by QuickLaTeX.com \[ \lambda^*(A) \leq Total\_Len(\cup_i \mathscr{U}_i) = \sum_i Total\_Len(\mathscr{U}_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1e68f517aa9bc6ba0a53faced21041c9_l3.png)
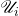 取下确界,可得
取下确界,可得![Rendered by QuickLaTeX.com \[ \lambda^*(A) \leq \sum_i \lambda^*(A_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-72c15159d982f053d3dfaec854446da2_l3.png)
- (空集)我们有
- (Lebesgue外测度)类似地,在计算机图形学的重心坐标中,光线追踪的BVH(Bounding Volume Hierarchy,包围体积层次结构)用AABB(Axis-Aligned Bounding Box,沿坐标轴对齐的包围盒)来包围
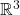 中的三角形网格;在这里,我们用开的AABB来覆盖
中的三角形网格;在这里,我们用开的AABB来覆盖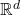 中的集合,
中的集合,![Rendered by QuickLaTeX.com \[ \lambda^*: \mathscr{P}(\mathbb{R}^d) \to [0, +\infty],\; \lambda^*(A) = \inf_{A \subset \cup_i I_i} \sum_i Vol(I_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1f65a28205a68166239eeef1af5c8ecc_l3.png)
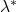 称为
称为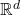 上的Lebesgue外测度,它的性质和上面相同
上的Lebesgue外测度,它的性质和上面相同
- (空集)我们有
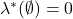
- (单调性)如果
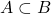 ,那么
,那么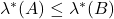
- (可数次可加性)如果
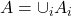 ,那么
,那么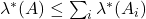
- (空集)我们有
- (Lebesgue外测度是体积的推广)设
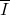 为闭的AABB,那么它的Lebesgue外测度等于它的体积。注意,AABB –> 沿坐标轴对齐,立方体 –> 不一定沿坐标轴对齐;对于后者,我们需要考虑AABB的仿射变换
为闭的AABB,那么它的Lebesgue外测度等于它的体积。注意,AABB –> 沿坐标轴对齐,立方体 –> 不一定沿坐标轴对齐;对于后者,我们需要考虑AABB的仿射变换
- 一方面,用一个体积更大的、开的AABB来覆盖
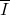 ,使得
,使得
令![Rendered by QuickLaTeX.com \[ \lambda^*(\overline{I}) \leq Vol(\overline{I}) + \epsilon. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-644a17551f1536c70375249a322d3f1e_l3.png)
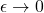 ,可得
,可得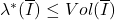
- 另一方面,由实数的完备性可知,
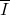 为紧的。因此,对于
为紧的。因此,对于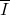 的任意一个开的AABB覆盖
的任意一个开的AABB覆盖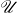 ,存在一个有限覆盖
,存在一个有限覆盖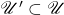 。将
。将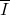 分解为有限个子AABB,使得它们都包含在
分解为有限个子AABB,使得它们都包含在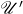 中的某个AABB中。从而, 我们有体积不等式
中的某个AABB中。从而, 我们有体积不等式
对所有![Rendered by QuickLaTeX.com \[ Vol(\overline{I}) \leq Total\_Vol(\mathscr{U}') \leq Total\_Vol(\mathscr{U}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b31cbf601b11ff47f7e642b75b385689_l3.png)
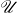 取下确界,可得
取下确界,可得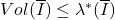
- 一方面,用一个体积更大的、开的AABB来覆盖
Lebesgue测度
- 尽管Lebesgue外测度的确是体积的一种推广,然而它只有次可加性,我们希望得到可加性。一种方法是只考虑满足可加性的集合
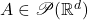 ,
,
这称为Carathéodory判别准则——对于不相交的集合![Rendered by QuickLaTeX.com \[ \lambda^*(B) = \lambda^*(A \cap B) + \lambda^*(A^c \cap B) \text{ for any } B \in \mathscr{P}(\mathbb{R}^d). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d1201ac3283b4558b246755f9fe55280_l3.png)
 、
、 ,它们的Lebesgue外测度可以相加
,它们的Lebesgue外测度可以相加 - 满足Carathéodory判别准则的集合,称为Lebesgue可测集,它们构成一个子族
由![Rendered by QuickLaTeX.com \[ \mathscr{M}_{\lambda^*} \subset \mathscr{P}(\mathbb{R}^d). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1ab3be325eb42d6138ff02dd8098be1b_l3.png)
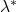 的次可加性,我们只需检验
的次可加性,我们只需检验
一个典型的例子是Lebesgue外测度为0的集合,称为零测集。如果![Rendered by QuickLaTeX.com \[ \lambda^*(B) \geq \lambda^*(A \cap B) + \lambda^*(A^c \cap B) \text{ for any } B \in \mathscr{P}(\mathbb{R}^d). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3a3bebb4344119f1a5fa68a658c0a18d_l3.png)
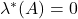 ,那么
,那么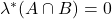 。因此,
。因此, 满足Carathéodory判别准则,
满足Carathéodory判别准则,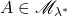
- (空集)
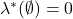 ,所以
,所以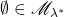
- (超平面)沿坐标轴对齐的超平面
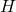 可以用总体积任意小的、开的AABB来覆盖,
可以用总体积任意小的、开的AABB来覆盖,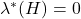 ,所以
,所以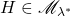
- (半空间)沿坐标轴对齐的超平面
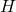 将
将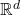 划分为两个开的半空间
划分为两个开的半空间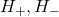 。对于
。对于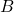 的任意一个开的AABB覆盖,我们可以沿着
的任意一个开的AABB覆盖,我们可以沿着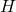 将其划分为两个开的AABB覆盖,分别覆盖
将其划分为两个开的AABB覆盖,分别覆盖
因此,![Rendered by QuickLaTeX.com \[ H_+ \cap B,\; H_- \cap B. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4df0f2b22162ab1c7dac55d222e55e72_l3.png)
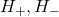 满足Carathéodory判别准则,
满足Carathéodory判别准则,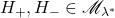
- (空集)
- 对于Lebesgue可测集,Lebesgue外测度
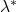 提升为Lebesgue测度
提升为Lebesgue测度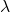 ,它满足可加性。为此,我们还需要先说明相应的集合为Lebesgue可测集
,它满足可加性。为此,我们还需要先说明相应的集合为Lebesgue可测集
- (补集)如果
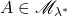 ,那么
,那么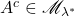
- (有限并)如果
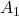 、
、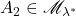 ,那么利用Carathéodory判别准则,
,那么利用Carathéodory判别准则,
由于![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \lambda^*(B) &= \lambda^*(A_1 \cap B) + \lambda^*(A_1^c \cap B) \\ &= \lambda^*(A_1 \cap B) + \lambda^*[A_2 \cap (A_1^c \cap B)] + \lambda^*[A_2^c \cap (A_1^c \cap B)]. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-92426024b7773e97a2cf4da0539a7e6b_l3.png)
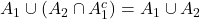 、
、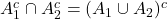 ,故
,故
因此,![Rendered by QuickLaTeX.com \[ \lambda^*(B) \geq \lambda^*[(A_1 \cup A_2) \cap B] + \lambda^*[(A_2 \cup A_1)^c \cap B]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9295d0f4cf1d5b18fdf52029e4f01ee1_l3.png)
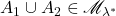 。利用数学归纳法,可得有限并。进一步,利用补集、有限并,可得有限交
。利用数学归纳法,可得有限并。进一步,利用补集、有限并,可得有限交 - (有限可加性)如果
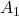 、
、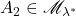 ,并且二者不相交,那么
,并且二者不相交,那么
利用数学归纳法,可得有限可加性![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \lambda(A_1 \cup A_2) &= \lambda[A_1 \cap (A_1 \cup A_2)] + \lambda[A_1^c \cap (A_1 \cup A_2)] \\ &= \lambda(A_1) + \lambda(A_2). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-de236686c7bf3a3885bb689a4ade742e_l3.png)
- (可数并)对于
 ,不妨设它们两两不相交。否则,我们可以考虑并集相同的、两两不相交的集合
,不妨设它们两两不相交。否则,我们可以考虑并集相同的、两两不相交的集合
利用有限可加性,![Rendered by QuickLaTeX.com \[ A_1, A_2 \cap A_1^c, A_3 \cap (A_1 \cup A_2)^c \ldots \in \mathscr{M}_{\lambda^*}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6e37218c6395259a3d568fb4be2107f8_l3.png)
令![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \lambda^*(B) &= \lambda^*[(\cup_{i = 1}^n A_i) \cap B] + \lambda^*[(\cup_{i = 1}^n A_i)^c \cap B] \\ &= \sum_{i = 1}^n \lambda^*(A_i \cap B) + \lambda^*[(\cup_{i = 1}^n A_i)^c \cap B] \\ &\geq \sum_{i = 1}^n \lambda^*(A_i \cap B) + \lambda^*[(\cup_{i = 1}^\infty A_i)^c \cap B]. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a141fcc0bbd3d8f26d23bc37aeb00717_l3.png)
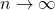 ,可得
,可得
因此,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \lambda^*(B) &\geq \sum_{i = 1}^\infty \lambda^*(A_i \cap B) + \lambda^*[(\cup_{i = 1}^\infty A_i)^c \cap B] \\ &\geq \lambda^*[(\cup_{i = 1}^\infty A_i) \cap B] + \lambda^*[(\cup_{i = 1}^\infty A_i)^c \cap B]. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dee17422a6f9467da953fb736cb5d92b_l3.png)
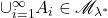 。进一步,利用补集、可数并,可得可数交
。进一步,利用补集、可数并,可得可数交 - (可数可加性)利用有限可加性,
令![Rendered by QuickLaTeX.com \[ \lambda(\cup_{i = 1}^\infty A_i) \geq \lambda(\cup_{i = 1}^n A_i) = \sum_{i = 1}^n \lambda(A_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-edb5a955013040e753fc604eae119e99_l3.png)
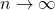 ,可得
,可得
相反方向的不等式可以由可数次可加性得到![Rendered by QuickLaTeX.com \[ \lambda(\cup_{i = 1}^\infty A_i) \geq \sum_{i = 1}^\infty \lambda(A_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d71dd52fb42ad8f5a72d6da4f4880420_l3.png)
- (补集)如果
- 有了补集、可数并,我们可以得到更多的Lebesgue可测集
- 半空间 –> (有限交) –> 开的AABB –> (可数并) –> 开集 –> (补集、可数并) –> Borel集
- 一个Lebesgue可测集,用一列开的AABB覆盖来趋近它的Lebesgue测度。如果取这一列开覆盖的可数交,那么可以得到一个Borel集,它和Lebesgue可测集只相差一个零测集
- 仿射变换为同胚,它将Borel集变为Borel集;由下面的计算可知,它将零测集变为零测集。因此,仿射变换将Lebesgue可测集变为Lebesgue可测集(仿射变换也可以减弱为Jacobi矩阵有界的
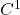 微分同胚)
微分同胚)
- 有了可数可加性,我们可以计算更多的Lebesgue测度
- 设
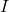 为开的AABB,它的边界
为开的AABB,它的边界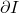 包含在有限个超平面中,所以为零测集。因此,
包含在有限个超平面中,所以为零测集。因此,
类似地,对于![Rendered by QuickLaTeX.com \[ \lambda(I) = \lambda(I) + \lambda(\partial I) = \lambda(\overline{I}) = Vol(\overline{I}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3df3c11b18895d8c3b5248bbd7cdaa33_l3.png)
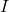 和部分边界的并集,它的Lebesgue测度也等于它的体积
和部分边界的并集,它的Lebesgue测度也等于它的体积 - 由计算机图形学的几何变换可知,仿射变换可以由平移、伸缩、切变、镜面反射生成。设
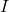 为开的AABB
为开的AABB
- 如果
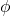 为平移、伸缩、镜面反射,那么
为平移、伸缩、镜面反射,那么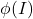 也为AABB,并且
也为AABB,并且![Rendered by QuickLaTeX.com \[ \lambda[\phi(I)] = |\det(D\phi)| \cdot \lambda(I). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4c38c20ecc48aa702ac00ce4e95e435b_l3.png)
- 如果
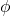 为切变,那么
为切变,那么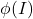 在切变的两个维度上,由AABB变为平行四边形。在平面几何中,我们可以利用面积割补法,证明平行四边形的面积等于AABB的面积,这本质上是Lebesgue测度的可加性。因此,我们有
在切变的两个维度上,由AABB变为平行四边形。在平面几何中,我们可以利用面积割补法,证明平行四边形的面积等于AABB的面积,这本质上是Lebesgue测度的可加性。因此,我们有![Rendered by QuickLaTeX.com \[ \lambda[\phi(I)] = |\det(D\phi)| \cdot \lambda(I). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4c38c20ecc48aa702ac00ce4e95e435b_l3.png)
- 如果
- 对于一般的Lebesgue可测集
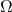 、一般的仿射变换
、一般的仿射变换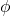 ,我们也有
,我们也有
这里,Jacobi矩阵![Rendered by QuickLaTeX.com \[ \lambda[\phi(\Omega)] = |\det(D\phi)| \cdot \lambda(\Omega). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e23f42f476a9fbf3d9412179f10d89cb_l3.png)
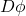 等于
等于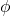 的可逆的线性变换部分。因为仿射变换可以由平移、伸缩、切变、镜面反射生成,所以我们只需考虑
的可逆的线性变换部分。因为仿射变换可以由平移、伸缩、切变、镜面反射生成,所以我们只需考虑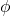 为四种情形之一
为四种情形之一
- 如果
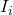 为
为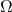 的开的AABB覆盖,那么
的开的AABB覆盖,那么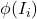 为
为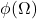 的开覆盖。因此,
的开覆盖。因此,
对所有![Rendered by QuickLaTeX.com \[ \lambda[\phi(\Omega)] \leq \sum_i \lambda[\phi(I_i)] = |\det(D\phi)| \cdot \sum_i \lambda(I_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-652b1fbe5e41262f04dfc8bc742b2f9b_l3.png)
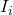 取下确界,可得
取下确界,可得![Rendered by QuickLaTeX.com \[ \lambda[\phi(\Omega)] \leq |\det(D\phi)| \cdot \lambda(\Omega). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-60892cc52f8085312e766b64a02244b7_l3.png)
- 对于相反方向的不等式,我们使用逆变换
![Rendered by QuickLaTeX.com \[ \lambda(\Omega) \leq |\det(D\phi^{-1})| \cdot \lambda[\phi(\Omega)]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-169f6d39185981e4be4c078ffbe765b3_l3.png)
- 如果
- 设