二进制编码
- 关于编码,可参见Shannon熵。关于一般的域上的线性空间,可参见数值线性代数
- 二进制串的集合为
它是一个![Rendered by QuickLaTeX.com \[ \mathbb{F}_2^n = \{ x = (x_1, \ldots, x_n) : x_i \in \mathbb{F}_2 \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b593df32c01403dc4c514924fe78c67e_l3.png)
 维
维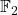 -线性空间,内积为
-线性空间,内积为
由二进制、逻辑和Boole代数可知,![Rendered by QuickLaTeX.com \[ x \cdot y = (x_1, \ldots, x_n) \cdot (y_1, \ldots, y_n) = \sum_{i = 1}^n x_iy_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e67cd9607215efcfbbb47df11ab31991_l3.png)
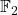 不是全序域。因此,由度量和拓扑可知,内积无法诱导度量,不过,我们可以使用其他度量
不是全序域。因此,由度量和拓扑可知,内积无法诱导度量,不过,我们可以使用其他度量 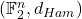 为一个度量空间,其中
为一个度量空间,其中
称为Hamming码距![Rendered by QuickLaTeX.com \[ d_{Ham}(x, y) = card(\{ i : x_i \neq y_i \}) \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e1b83b891f34780a6fbb98b42b68ae82_l3.png)
- 只需证明三角不等式。注意到
因此,![Rendered by QuickLaTeX.com \[ x_i \neq z_i \Rightarrow x_i \neq y_i \text{ or } y_i \neq z_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fa86cfd11c4262f1f3058a63339f60f6_l3.png)
![Rendered by QuickLaTeX.com \[ card(\{ i : x_i \neq z_i \}) \leq card(\{ i : x_i \neq y_i \}) + card(\{ i : y_i \neq z_i \}), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7b1fc08f84ec10d88528d83557eec64a_l3.png)
![Rendered by QuickLaTeX.com \[ d_{Ham}(x, z) \leq d_{Ham}(x, y) + d_{Ham}(y, z). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1d41f62b2e782951d157b49ea859efaa_l3.png)
- 只需证明三角不等式。注意到
- 二进制编码
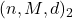 满足如下条件
满足如下条件
- 基本码字
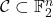
- 基本码字的个数为
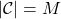
- 不同基本码字之间的最小距离为
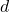
- 基本码字
- 在距离空间
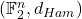 中,考虑一族互不相交的、半径为
中,考虑一族互不相交的、半径为![Rendered by QuickLaTeX.com e = [(d - 1) / 2]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0d9176a9b9da54d39f2b247b5f0ef382_l3.png) 的闭球
的闭球
如果一个二进制串![Rendered by QuickLaTeX.com \[ \{ \overline{B}(x, e) : x \in \mathcal{C} \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d5c8391d0dc63eba33906ee594e6755c_l3.png)
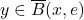 ,那么
,那么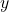 和
和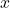 至多相差
至多相差 位,
位,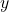 可以纠错为
可以纠错为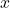 。因为最小距离
。因为最小距离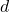 确定了纠错位数
确定了纠错位数 ,所以在实际的通信中,我们希望
,所以在实际的通信中,我们希望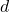 越大越好
越大越好
扩展到一般线性编码
- 我们可以将
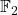 扩展到一般的有限域。由有限域的阶可知,我们可取有限域
扩展到一般的有限域。由有限域的阶可知,我们可取有限域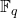 ,其中
,其中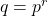 ,
, 为素数。此时,
为素数。此时,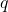 阶串的集合为
阶串的集合为
它是一个![Rendered by QuickLaTeX.com \[ \mathbb{F}_q^n = \{ x = (x_1, \ldots, x_n) : x_i \in \mathbb{F}_q \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-44144685ae6fd869a59a4dda39417d82_l3.png)
 维
维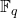 -线性空间
-线性空间 - 一般线性编码
![Rendered by QuickLaTeX.com [n, k, d]_q](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-865f99cf851c813c11e926b83f42924e_l3.png) 满足如下条件
满足如下条件
- 基本码字
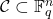 为线性子空间
为线性子空间 - 基本码字的个数为
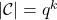 ,其中
,其中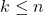 为线性子空间的维数
为线性子空间的维数 - 不同基本码字之间的最小距离为
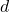
- 基本码字