Newton方程
- 质点的Newton方程为
其中![Rendered by QuickLaTeX.com \[ ma = F(r, v, t),\; v = \frac{dr}{dt},\; a = \frac{dv}{dt} = \frac{d^2r}{dt^2}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bb297091e6e6e28538d2b2f77f338193_l3.png)
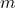 为质量,
为质量, 为力,
为力, 、
、 、
、 分别为位置向量、速度、加速度
分别为位置向量、速度、加速度- 如果
 已知,那么由ODE的结果可知,给定初值
已知,那么由ODE的结果可知,给定初值
Newton方程存在唯一解![Rendered by QuickLaTeX.com \[ r(t_0) = r_0,\; v(t_0) = v_0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e9ed5bf812bb5462bff1a3a3559c4020_l3.png)
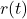
- 守恒定律
- 保守力场的能量守恒定律
- 保守力场满足
其中,![Rendered by QuickLaTeX.com \[ F = -\nabla V(r), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bf61ced5fd394189cfe3003277983847_l3.png)
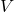 为势能
为势能 - 动能、总能量分别为
由Newton方程,![Rendered by QuickLaTeX.com \[ T = \frac 12mv^2,\; E = T + V. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c701aec32fdce41c659709b9521697a9_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{dE}{dt} = ma \cdot v + \nabla V(r) \cdot v = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bd6c3da60a1353d402e9eee1b62d2421_l3.png)
![Rendered by QuickLaTeX.com \[ E = const. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5d408673579cac1cc587eb92f66abbee_l3.png)
- 保守力场满足
- 向心保守力场的角动量守恒定律
- 向心保守力场满足
![Rendered by QuickLaTeX.com \[ F = -\nabla V(|r|) = -\frac{dV}{d|r|}\frac{r}{|r|}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5bd0482e918525ffcf1c4468dc889b2a_l3.png)
- 角动量为
由Newton方程,![Rendered by QuickLaTeX.com \[ L = r \times mv. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-789db5fe56171f151983aecfdf65d069_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{dL}{dt} = v \times mv + r \times \bigg(-\frac{dV}{d|r|}\frac{r}{|r|}\bigg) = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-79b1d4deb39b0f66e66797d3339c30a2_l3.png)
![Rendered by QuickLaTeX.com \[ L = const. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ed67baf3f585875bacf02e383c6f926a_l3.png)
- 向心保守力场满足
- 孤立系统的动量守恒定律
- 孤立系统满足
其中,![Rendered by QuickLaTeX.com \[ F_i = \sum_{j \neq i} F_{ji},\; F_{ji} = -F_{ij}\; (j \neq i), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-416d4dceb602276ea33afc7e07620f73_l3.png)
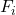 为作用于质点
为作用于质点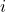 的力,
的力,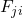 为质点
为质点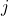 作用于质点
作用于质点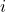 的力
的力 - 动量为
由Newton方程,![Rendered by QuickLaTeX.com \[ P = \sum_i m_iv_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-070c8104daed09b575d87c0207e36e9a_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{dP}{dt} = \sum_i\sum_{j \neq i} F_{ji} = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-afac6bed9144bc536bec9be4b79749a2_l3.png)
![Rendered by QuickLaTeX.com \[ P = const. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9d0e9fa8728abc2d6490d8fd09cae4b1_l3.png)
- 孤立系统满足
- 保守力场的能量守恒定律
相对性原理
- 关于Galileo变换群、Poincaré变换群,可参见矩阵群
- Galileo相对性原理
- 在孤立系统、向心保守力场中,Newton方程为
![Rendered by QuickLaTeX.com \[ m_i\frac{d^2r_i}{dt^2} = -\sum_{j \neq i} \nabla_i V(\ldots, |r_i - r_j|, \ldots) = -\sum_{j \neq i} \frac{\partial V}{\partial|r_i - r_j|}\frac{r_i - r_j}{|r_i - r_j|}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-13879ca9ec9732680f75bcc56eedd21e_l3.png)
- 如下的Galileo变换将解变为解,
Galileo变换群为![Rendered by QuickLaTeX.com \[ \begin{bmatrix}R & v \\ 0 & 1\end{bmatrix} \cdot \begin{bmatrix}r \\ t\end{bmatrix} + \begin{bmatrix}r_0 \\ t_0\end{bmatrix} = \begin{bmatrix}r' \\ t'\end{bmatrix},\; R \in O(3),\; v \in \mathbb{R}^3. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d9b11644b519e745a35ad6d1df546832_l3.png)
![Rendered by QuickLaTeX.com \mathbb{R}^4 \rtimes [\mathbb{R}^3 \rtimes O(3)]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c99dd8bd93be24572fc5d734e605d0bc_l3.png) ,其中,可逆的线性变换部分为Euclid群
,其中,可逆的线性变换部分为Euclid群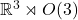
- 在孤立系统、向心保守力场中,Newton方程为
- 狭义相对性原理
- 在Minkowski时空中,光速不变的方程为
![Rendered by QuickLaTeX.com \[ dr^2 - c^2dt^2 = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d9d47d2f5b002f49958bfdf825853077_l3.png)
- 如下的Poincaré变换将解变为解,
Poincaré变换群为![Rendered by QuickLaTeX.com \[ A \cdot \begin{bmatrix}r \\ ct\end{bmatrix} + \begin{bmatrix}r_0 \\ ct_0\end{bmatrix} = \begin{bmatrix}r' \\ ct'\end{bmatrix},\; A \in O(3, 1). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8151be725d4d4a959d7d929d02d4e7d4_l3.png)
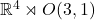 ,其中,可逆的线性变换部分为Lorentz群
,其中,可逆的线性变换部分为Lorentz群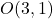
- 在Minkowski时空中,光速不变的方程为
最小作用量原理
- 在保守力场中,作用量为
泛函![Rendered by QuickLaTeX.com \[ \mathcal{S} = \int_{t_1}^{t_2} (T - V)dt = \int_{t_1}^{t_2} \bigg[\frac 12mv^2 - V(r)\bigg]dt. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-12b88f6e848fa66192e86d2776c14c9a_l3.png)
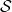 的变分为
的变分为
因此,当端点固定时,泛函![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \delta\mathcal{S} &= \int_{t_1}^{t_2} \bigg[mv \cdot \delta v - \nabla V(r) \cdot \delta r\bigg]dt \\ &= \int_{t_1}^{t_2} \bigg[mv \cdot \frac{d\delta r}{dt} + F \cdot \delta r\bigg]dt \\ &= mv \cdot \delta r\bigg|_{t_1}^{t_2} + \int_{t_1}^{t_2} (-ma + F) \cdot \delta rdt. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c6a83acdadf8f1a494dd357ae3e4d126_l3.png)
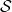 在Newton方程的解上达到临界值
在Newton方程的解上达到临界值 - 一般地,作用量为
其中,![Rendered by QuickLaTeX.com \[ \mathcal{S} = \int_{t_1}^{t_2} \mathcal{L}(q, \dot{q}, t)dt, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-71c2dd517314abc8c58f9bb29f2a5b84_l3.png)
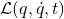 为在广义坐标
为在广义坐标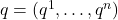 、广义速度
、广义速度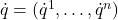 下的Lagrangian。泛函
下的Lagrangian。泛函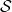 的变分为
的变分为
因此,当端点固定时,泛函![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \delta\mathcal{S} &= \int_{t_1}^{t_2} \bigg[\frac{\partial\mathcal{L}}{\partial\dot{q}} \cdot \delta \dot{q} + \frac{\partial\mathcal{L}}{\partial q} \cdot \delta q\bigg]dt \\ &= \int_{t_1}^{t_2} \bigg[\frac{\partial\mathcal{L}}{\partial\dot{q}} \cdot \frac{d\delta q}{dt} + \frac{\partial\mathcal{L}}{\partial q} \cdot \delta q\bigg]dt \\ &= \frac{\partial\mathcal{L}}{\partial\dot{q}} \cdot \delta q \bigg|_{t_1}^{t_2} + \int_{t_1}^{t_2} \bigg[-\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial\dot{q}} + \frac{\partial\mathcal{L}}{\partial q}\bigg] \cdot \delta qdt. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6a9062c6ef7339d314b8aed93c2bd277_l3.png)
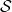 在如下的Euler-Lagrange方程的解上达到临界值,
在如下的Euler-Lagrange方程的解上达到临界值,![Rendered by QuickLaTeX.com \[ \frac{d}{dt}\frac{\partial\mathcal{L}}{\partial\dot{q}} - \frac{\partial\mathcal{L}}{\partial q} = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-da4db08e11e337a9940d658b7768fc42_l3.png)