佚名

网络的随机模型

通信系统概述

  • 有线传输
    • 同轴电缆
    • 双绞线
    • 光纤
  • 无线传输
    • 微波视距
    • 卫星
      • 静止卫星（Geostationary Satellite）
      • 近地轨道（Low Earth Orbit，LEO）
      • 中地轨道（Medium Earth Orbit，MEO）
      • 闪电轨道（Molniya Orbit）
    • 蜂窝网络
      • 中央电话局（Telephone Central Office）
      • 移动交换中心（Mobile Switching Center）
      • 基站（Base Station）
      • 蜂窝（Cell）
      • 手机（Cell Phone）
    • 移动通信
      • 1G –> 模拟通信，电话
      • 2G –> 数字通信，短信
      • 3G –> 低速流量，上网
      • 4G –> 高速流量，App
    • 自组织网络
    • 无线传感器网络
  • 网络
    • 交换机
    • 输入链路、输出链路
    • 包交换网络 –> 头部、载荷、路由
    • 电路交换网络 –> 连接

包交换网络的离散模型

  • Bernoulli分布
    • 时间槽是等长的
    • 在一个时间槽中，有包的概率为p，无包的概率为1 - p
  • 几何分布 –> 第一个包的到达时间（First Arrival，FA）
    • 概率分布

          \[ \mathbb{P}(FA = i) = (1 - p)^{i - 1}p. \]

    • 数学期望

          \begin{equation*}\begin{split} \mathbb{E}[FA] &= \sum_{i = 1}^\infty i(1 - p)^{i - 1}p \\ &= -p\frac{d}{dp}\sum_{i = 1}^\infty (1 - p)^i \\ &= -p\frac{d}{dp}\bigg(\frac{1 - p}{1 - (1 - p)}\bigg) \\ &= -p\frac{d}{dp}\bigg(\frac 1p - 1\bigg) = \frac 1p. \end{split}\end{equation*}

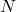  • 二项分布 –> 在N个时间槽中，包的到达数量（Number of Arrivals，NA）
    • 概率分布

          \[ \mathbb{P}(NA = i) = \binom{N}{i}p^i(1 - p)^{N - i}. \]

    • 数学期望

          \begin{equation*}\begin{split} \mathbb{E}[NA] &= \sum_{i = 0}^N i\binom{N}{i}p^i(1 - p)^{N - i} \\ &= p\sum_{i = 0}^N \binom{N}{i}\bigg(\frac{d}{dp}p^i\bigg) \cdot (1 - p)^{N - i} \\ &= -p\sum_{i = 0}^N \binom{N}{i}p^i \cdot \bigg(\frac{d}{dp}(1 - p)^{N - i}\bigg) \\ &= p\sum_{i = 0}^N (N - i)\binom{N}{i}p^i(1 - p)^{N - i - 1} \\ &= \frac{p}{1 - p}(N - \mathbb{E}[NA]). \end{split}\end{equation*}

      因此，

          \[ \mathbb{E}[NA] = Np. \]

以太网的设计