de Rham上同调群的定义

外形式、外微分算子

关于一般的域上的张量代数，可参见数值线性代数
由电磁场和de Rham上同调可知
- 我们可以考虑外微分算子 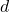$d$ ，它应该满足 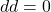$dd = 0$ 。进一步，它应该满足线性、Leibniz法则，以及Stokes定理
- 外积 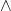$\wedge$ 为反对称性、线性的，它对应于行列式。正如行列式的展开具有交错和的形式，外微分算子 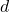$d$ 的展开也具有交错和的形式
- 外形式可以建立在一般的域上，微分形式可以建立在实数域、复数域上
外形式的集合既是环（乘法为 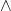$\wedge$ ），也是 $F$ -向量空间，故我们可以得到外代数，它是张量代数的 $F$ -子代数

de Rham上链复形、de Rham上同调群

外形式、外微分算子构成Abel群、Abel群的同态形成的序列
$\xymatrix@C=1.4em{ 0 \ar[r] & \Omega^0(M) \ar[r]^-{d_0} & \Omega^1(M) \ar[r] & \cdots \ar[r] & \Omega^n(M) \ar[r]^-{d_n} & \Omega^{n + 1}(M) \ar[r] & \cdots }$
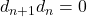满足 $d_{n + 1}d_n = 0$ 。这样的结构称为de Rham上链复形