微分形式
- 关于边缘算子,可参见奇异同调群的定义。关于外微分算子,可参见de Rham上同调群的定义
- Newton-Leibniz公式,1维情形
![Rendered by QuickLaTeX.com \[ \int_{[a, b]} f'(x)dx = f(b) - f(a). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-73369ea179309b7cb09c7909d4536617_l3.png)
- Newton-Leibniz公式,2维情形
令![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \int_{[c, d]}\int_{[a, b]} \partial_xf(x, y)dxdy &= \int_{[c, d]} [f(b, y) - f(a, y)]dy, \\ \int_{[a, b]}\int_{[c, d]} \partial_yg(x, y)dydx &= \int_{[a, b]} [g(x, d) - g(x, c)]dx. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-23dfc8345d5e7689cf6402c703e3ad63_l3.png)
![Rendered by QuickLaTeX.com \Omega = [a, b] \times [c, d]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a84f9b14dfc84416f9b2321b86f1b38a_l3.png) ,其边界
,其边界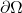 为
为
因此,![Rendered by QuickLaTeX.com \[ \xymatrix@C=1.4em{ (a, d) \ar[d]_{\Gamma_4} & (b, d) \ar[l]_{\Gamma_3} \\ (a, c) \ar[r]_{\Gamma_1} & (b, c) \ar[u]_{\Gamma_2} } \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-60641d1c232f7a69e8847ffc4abe553c_l3.png)
在![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \int_{[c, d]}\int_{[a, b]} \partial_xf(x, y)dxdy &= \int_{\Gamma_2} fdy + \int_{\Gamma_4} fdy, \\ \int_{[a, b]}\int_{[c, d]} \partial_yg(x, y)dydx &= -\int_{\Gamma_1} gdx - \int_{\Gamma_3} gdx. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3d471fae7bcaf9a9edf5083837669c84_l3.png)
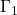 、
、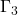 上,
上,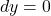 ,在
,在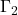 、
、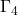 上,
上,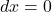 ,所以
,所以![Rendered by QuickLaTeX.com \[ \int_\Omega (\partial_xf - \partial_yg)dxdy = \int_{\partial\Omega} fdy + gdx. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ba545a25c492183b7d7e52fc54e45022_l3.png)
- 我们将1维情形改写为
如果令![Rendered by QuickLaTeX.com \[ \int_{[a, b]} df = \int_{\partial[a, b]}f. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2d0c58ddcedaeadb38bd6eee8683ddb2_l3.png)
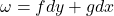 ,那么2维情形具有相同的形式
,那么2维情形具有相同的形式
这是一个配对,并且算子![Rendered by QuickLaTeX.com \[ \int_\Omega d\omega = \int_{\partial\Omega} \omega. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9163f7663223ec7342cadc60fe782be1_l3.png)
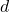 、
、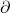 是伴随的,
是伴随的,![Rendered by QuickLaTeX.com \[ \langle{d\omega, \Omega}\rangle = \langle{\omega, \partial\Omega}\rangle. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fbee601b78ae3133aad008f6b7dcd382_l3.png)
- 现在我们讨论
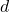 ,它应该类似于微分
,它应该类似于微分
- 因为
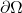 为
为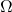 的边界,所以
的边界,所以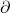 称为边缘算子。注意,
称为边缘算子。注意,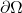 为闭曲线,其边界为0,即
为闭曲线,其边界为0,即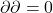 。利用伴随性,可得
。利用伴随性,可得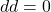 ,
,![Rendered by QuickLaTeX.com \[ \langle{dd\omega, \Omega}\rangle = \langle{d\omega, \partial\Omega}\rangle = \langle{\omega, \partial\partial\Omega}\rangle = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c853202d98946988f116756bec543531_l3.png)
- 令
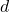 为线性算子,
为线性算子,
令![Rendered by QuickLaTeX.com \[ d\omega = d(fdy) + d(gdx). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0f64f1b75a24deb495688e8dd9709a30_l3.png)
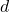 满足Leibniz法则(即乘法的微分公式),
满足Leibniz法则(即乘法的微分公式),
令乘法为反对称的,记为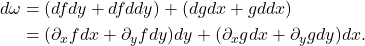
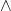 ,
,
最终,我们可以得到![Rendered by QuickLaTeX.com \[ dx \wedge dy = -dy \wedge dx,\; dx \wedge dx = 0,\; dy \wedge dy = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bf642ff1eaa4b7ff5830f4712be64609_l3.png)
![Rendered by QuickLaTeX.com \[ d\omega = (\partial_xf - \partial_yg)dx \wedge dy. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-184bed8bd10fc3ee166b5a94ca7d4a21_l3.png)
- 类似于计算机图形学的重心坐标,对于3维向量
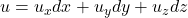 、
、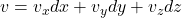 ,,我们有
,,我们有
因此,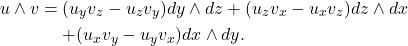
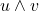 和
和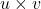 相同
相同
- 因为
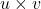 叫做外积,所以
叫做外积,所以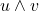 也叫做外积
也叫做外积 - 因为
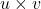 为反对称、线性的,它对应于行列式,所以
为反对称、线性的,它对应于行列式,所以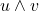 也一样
也一样
- 因为
- 进一步,
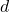 称为外微分算子,
称为外微分算子,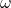 、
、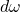 称为外形式(可以建立在一般的域上),或者微分形式(可以建立在实数域、复数域上)
称为外形式(可以建立在一般的域上),或者微分形式(可以建立在实数域、复数域上)
- 因为
微分形式和电磁场
- 关于
 、Stokes定理,可参见de Rham上同调群的定义
、Stokes定理,可参见de Rham上同调群的定义  上的外微分
上的外微分
- 0-形式的外微分对应于梯度(
 )
)![Rendered by QuickLaTeX.com \[ \omega = f,\; d\omega = \partial_xfdx + \partial_yfdy + \partial_zfdz. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-490bb650f135a3f6575ef2e3ad9e6b43_l3.png)
- 1-形式的外微分对应于旋度(curl)
![Rendered by QuickLaTeX.com \[ \omega = \omega_xdx + \omega_ydy + \omega_zdz, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e7c7553c73d0ca55a18735848cb04417_l3.png)
- 2-形式的外微分对应于散度(div)
![Rendered by QuickLaTeX.com \[ \omega = \omega_xdy \wedge dz + \omega_ydz \wedge dx + \omega_zdx \wedge dy, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bcba375d75aef8618c145a5031385879_l3.png)
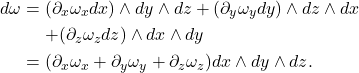
- 0-形式的外微分对应于梯度(
- 流形上的
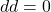
![Rendered by QuickLaTeX.com \[ dd\omega = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-68bb050e1c5a43cbda55191f03081751_l3.png)
- 0-形式的
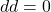 对应于梯度(
对应于梯度(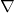 )、旋度(curl)
)、旋度(curl)![Rendered by QuickLaTeX.com \[ curl\nabla f = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ce1ff42c152864c597bc79ae310bcc09_l3.png)
- 1-形式的
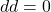 对应于旋度(curl)、散度(div)
对应于旋度(curl)、散度(div)![Rendered by QuickLaTeX.com \[ div\,curlX = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8fec7e3580d768592b3c92a9c060451a_l3.png)
- 在Maxwell方程组中,静电场的旋度(curl)使用了0-形式的
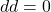 ,静磁场的散度(div)、电生磁使用了1-形式的
,静磁场的散度(div)、电生磁使用了1-形式的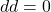
- 0-形式的
- 流形上的Stokes定理
![Rendered by QuickLaTeX.com \[ \int_{\partial\Omega} \omega = \int_\Omega d\omega. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b71b8708080d7b4c898f05df47181ad1_l3.png)
- 如果
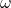 为1-形式,那么我们可以得到旋度(curl)的Stokes公式
为1-形式,那么我们可以得到旋度(curl)的Stokes公式![Rendered by QuickLaTeX.com \[ \int_{\partial\Omega} X \cdot dl = \int_\Omega curlX \cdot dS. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1c3ea60a4e37a60626ec74479e39d627_l3.png)
- 如果
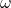 为2-形式,那么我们可以得到散度(div)的Gauss公式
为2-形式,那么我们可以得到散度(div)的Gauss公式![Rendered by QuickLaTeX.com \[ \int_{\partial\Omega} X \cdot dS = \int_\Omega divXdV. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8361e0eeb954ca6540fa62a9b4a76c03_l3.png)
- 在Maxwell方程组中,Faraday定律使用了旋度(curl)的Stokes公式,电荷守恒定律使用了散度(div)的Gauss公式
- 如果
de Rham上同调和电势、磁势
- 关于de Rham上同调群,可参见de Rham上同调群的定义
- 电势、磁势的存在性
- (电势)如果
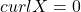 ,那么我们希望找到
,那么我们希望找到 ,使得
,使得
也就是说,如果![Rendered by QuickLaTeX.com \[ \nabla f = X. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a148e011113dd648b6b167a3d380e516_l3.png)
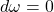 ,那么我们希望找到
,那么我们希望找到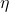 ,使得
,使得
因此,电势的存在性,等价于1维上闭链为1维上边缘链![Rendered by QuickLaTeX.com \[ d\eta = \omega. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2d23eed8d2ad3be789dc0f8e844fe9cb_l3.png)
- (磁势)如果
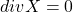 ,那么我们希望找到
,那么我们希望找到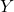 ,使得
,使得
也就是说,如果![Rendered by QuickLaTeX.com \[ curlY = X. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-285fb5a99e26b9d0fce8c6e5a3b2e2a1_l3.png)
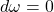 ,那么我们希望找到
,那么我们希望找到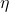 ,使得
,使得
因此,磁势的存在性,等价于2维上闭链为2维上边缘链![Rendered by QuickLaTeX.com \[ d\eta = \omega. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2d23eed8d2ad3be789dc0f8e844fe9cb_l3.png)
- 但是上闭链不一定是上边缘链,de Rham上同调群反映了从上闭链到上边缘链的障碍,
因此,电势、磁势的存在性,分别需要1维、2维de Rham上同调群为0![Rendered by QuickLaTeX.com \[ H_{dR}^n(M) = kerd_n/imd_{n - 1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9a915cbe6c8d28dee1c987dbc205106b_l3.png)
- (电势)如果
- 由de Rham定理,
因此,电势、磁势的存在性,分别需要所在空间的1维、2维奇异上同调群为0。这一结论的意义在于,空间中的势场的存在性,可以由空间本身的拓扑确定![Rendered by QuickLaTeX.com \[ H_{dR}^k(M) \cong H^k(M; \mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3afb3276e3fc3d0d38fe92d721624f5a_l3.png)
- 在天线理论的电磁波中,求解射频的电磁波使用了电势、磁势的存在性。如果所在空间为3维空间,即
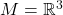 ,那么它可以形变收缩至一点。此时,所在空间的拓扑是平凡的,1维、2维奇异上同调群为0,所以电势、磁势存在
,那么它可以形变收缩至一点。此时,所在空间的拓扑是平凡的,1维、2维奇异上同调群为0,所以电势、磁势存在 - 如果所在空间为3维空间去掉一个点,即
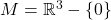 ,那么它可以形变收缩至
,那么它可以形变收缩至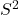 。利用
。利用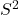 的2维奇异同调群和Poincaré对偶(?),
的2维奇异同调群和Poincaré对偶(?),
因此,电势可能不存在,但是磁势总是存在![Rendered by QuickLaTeX.com \[ \mathbb{R} \cong H_2(M; \mathbb{R}) \cong H^1(M; \mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e3572bd0e4f2637d05546a781f5ae2ef_l3.png)
- 如果所在空间为3维空间去掉一条直线,即
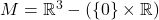 ,那么它可以形变收缩至
,那么它可以形变收缩至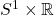 。利用
。利用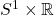 的1维奇异同调群和Poincaré对偶(?),
的1维奇异同调群和Poincaré对偶(?),
因此,磁势可能不存在,但是电势总是存在![Rendered by QuickLaTeX.com \[ \mathbb{R} \cong H_1(M; \mathbb{R}) \cong H^2(M; \mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-43d887e99c74839c815c895189e2d6c5_l3.png)
- 在天线理论的电磁波中,求解射频的电磁波使用了电势、磁势的存在性。如果所在空间为3维空间,即
- 在de Rham上同调和Dolbeault上同调中,我们使用层的上同调,得到de Rham定理