参考资料:复变函数简明教程
Cauchy-Riemann方程
- 关于实数域上的分析,以及流形,可参见从切空间到局部、从局部到整体
- 复数域和实数域类似,可以进行加法、减法、乘法、除法。我们从差分开始
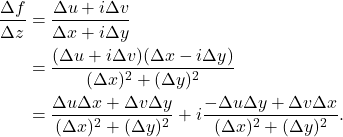
- 如果
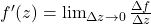 存在,那么
存在,那么
因此,我们可以得到Cauchy-Riemann方程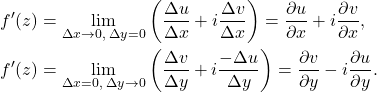
![Rendered by QuickLaTeX.com \[ \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y},\; \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-584545f77f6ab6d30bb34e4ae558c7d9_l3.png)
- 反过来,如果Cauchy-Riemann方程成立,那么
取极限,可得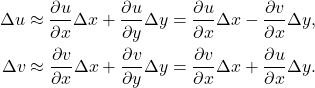
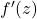 存在
存在![Rendered by QuickLaTeX.com \[ f'(z) = \lim_{\Delta z \to 0} \frac{\Delta f}{\Delta z} = \frac{\partial u}{\partial x} + i\frac{\partial v}{\partial x}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e54a314e1c451ff977fdccaee5343565_l3.png)
- 因此,
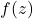 存在导数,等价于Cauchy-Riemann方程成立,并且复数域和实数域的求导法则(比如四则运算、复合函数、反函数)是相同的
存在导数,等价于Cauchy-Riemann方程成立,并且复数域和实数域的求导法则(比如四则运算、复合函数、反函数)是相同的
Cauchy积分定理、Cauchy积分公式
- 复数域和实数域类似,可以得到流形。上面,
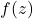 是可微的;在PDE的解的正则性中,
是可微的;在PDE的解的正则性中,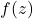 的正则性可以提升到光滑,所以我们可以考虑复流形上的分析
的正则性可以提升到光滑,所以我们可以考虑复流形上的分析 - 我们有切向量、余切向量
- (余切向量)由
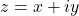 ,
,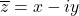 ,可得
,可得![Rendered by QuickLaTeX.com \[ dz = dx + idy,\; d\overline{z} = dx - idy. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b572020a94c2afd9b33e84eb9afbdc7a_l3.png)
- (切向量)取对偶基底,可得
![Rendered by QuickLaTeX.com \[ \frac{\partial}{\partial z} = \frac 12\bigg(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\bigg),\; \frac{\partial}{\partial \overline{z}} = \frac 12\bigg(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\bigg). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e339a49a54b8ed051582404c2551f071_l3.png)
- Cauchy-Riemann方程等价于如下的形式
也就是说,![Rendered by QuickLaTeX.com \[ \frac{\partial f}{\partial\overline{z}} = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-de41807eee6142362c23b752f243317f_l3.png)
 与
与 无关,纯粹是
无关,纯粹是 的函数,所以称为全纯函数(Holomorphic Function)。非全纯函数是普遍存在的,比如
的函数,所以称为全纯函数(Holomorphic Function)。非全纯函数是普遍存在的,比如
不是全纯函数,它与![Rendered by QuickLaTeX.com \[ f(z, \overline{z}) = |z|^2 = z\overline{z} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-65002f88d78deb5fe316e1c229ce3d1a_l3.png)
 有关,不满足Cauchy-Riemann方程
有关,不满足Cauchy-Riemann方程
- (余切向量)由
- 进一步,我们有微分形式、微分算子
- (微分形式)面积元素的复数形式
![Rendered by QuickLaTeX.com \[ dz \wedge d\overline{z} = (dx + idy) \wedge (dx - idy) = -2idx \wedge dy. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8c54ce354893320f80dbd3e23cf52ff9_l3.png)
- (微分算子)Laplace算子的复数形式
![Rendered by QuickLaTeX.com \[ \frac{\partial}{\partial z}\frac{\partial}{\partial \overline{z}} = \frac 14\bigg(\frac{\partial}{\partial x} - i\frac{\partial}{\partial y}\bigg)\bigg(\frac{\partial}{\partial x} + i\frac{\partial}{\partial y}\bigg) = \frac 14\Delta. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ab910ac16a7aad8c28ebdc1daf235708_l3.png)
- (微分形式)面积元素的复数形式
- 对于全纯函数,Cauchy积分定理源于微分形式,Cauchy积分公式源于微分算子、基本解。在使用Fourier变换求解PDE中,我们可以得到Laplace算子在
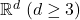 上的基本解;在这里,我们可以得到Laplace算子在
上的基本解;在这里,我们可以得到Laplace算子在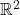 上的基本解
上的基本解
- (Cauchy积分定理)由Stokes定理,令
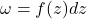 ,
,![Rendered by QuickLaTeX.com \[ \int_{\partial\Omega} f(z)dz = \int_{\partial\Omega} \omega = \int_\Omega d\omega = \int_\Omega \frac{\partial f}{\partial\overline{z}}d\overline{z} \wedge dz = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1ac96114bb6fe2040ebfab835bfe66c4_l3.png)
- (基本解)类似于天线理论的电磁波,令
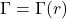 ,那么
,那么
因此,我们可以得到非常数的基本解![Rendered by QuickLaTeX.com \[ 0 = \Delta\Gamma = \frac{d^2\Gamma}{dr^2} + \frac 1r\frac{d\Gamma}{dr},\; r \neq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b5196d63da1cffd7dc4d9c05c14f0ddb_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{d\Gamma}{dr} = C\frac 1r,\; \Gamma = C\ln r. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8c9ba3256b042b07950425879cac533b_l3.png)
- (Cauchy积分公式)注意,
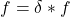 ,
,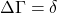 。由Stokes定理,
。由Stokes定理,
同时,由![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} f(w) &= \int_{B_\epsilon(w)} \Delta\Gamma(w - z, \overline{w} - \overline{z}) \cdot f(z)dx \wedge dy \\ &= \int_{B_\epsilon(w)} -4\frac{\partial}{\partial \overline{z}}\bigg[\frac{\partial}{\partial z}\Gamma(w - z, \overline{w} - \overline{z}) \cdot f(z)\bigg] \cdot \frac i2dz \wedge d\overline{z} \\ &= 2i\int_{\partial B_\epsilon(w)} \frac{\partial}{\partial z}\Gamma(w - z, \overline{w} - \overline{z}) \cdot f(z)dz. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-57adbe3afed69f518e806a95548ca244_l3.png)
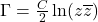 ,我们可以得到Cauchy核
,我们可以得到Cauchy核
因此,Cauchy核与![Rendered by QuickLaTeX.com \[ \frac{\partial \Gamma}{\partial z} = \frac C2\frac{1}{z\overline{z}} \cdot \overline{z} = \frac C2\frac 1z. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0574aa9ac9d8d07f522cc520f9b3c8f8_l3.png)
 (在边界上)卷积之后为
(在边界上)卷积之后为 本身
本身![Rendered by QuickLaTeX.com \[ f(w) = -iC\int_{\partial B_\epsilon(w)} \frac{f(z)}{z - w}dz. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2db668d70abfa1d03fca5701b3a1be23_l3.png)
- 作为Cauchy积分公式的特殊情形,令
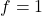 ,
,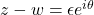 。那么,
。那么,
因此,基本解为![Rendered by QuickLaTeX.com \[ 1 = -iC\int_0^{2\pi} \frac{1}{\epsilon e^{i\theta}} \cdot \epsilon e^{i\theta}id\theta = 2\pi C \Rightarrow C = \frac{1}{2\pi}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bfab60180519709723a2f9051f125cd5_l3.png)
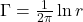 ,Cauchy积分公式为
,Cauchy积分公式为![Rendered by QuickLaTeX.com \[ f(w) = \frac{1}{2\pi i}\int_{\partial B_\epsilon(w)} \frac{f(z)}{z - w}dz. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a6b2abb0d23bb314ed936210ace2a54a_l3.png)
- (Cauchy积分定理)由Stokes定理,令
- Cauchy积分定理 –> 没有奇点的情形,Cauchy积分公式 –> 有奇点的情形。在Maxwell方程组中,点电荷、点磁荷可以用
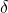 来刻画;在这里,奇点可以用
来刻画;在这里,奇点可以用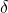 来刻画
来刻画
全纯同胚、分歧覆盖映射
- (解析函数)复数域和实数域的第一个不同点,在于全纯函数一定为解析函数
- Cauchy积分公式有一个奇点
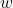 。不过,它不在
。不过,它不在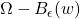 中,所以我们可以使用Cauchy积分定理,
中,所以我们可以使用Cauchy积分定理,![Rendered by QuickLaTeX.com \[ 0 = \frac{1}{2\pi i}\int_{\partial(\Omega - B_\epsilon(w))} \frac{f(z)}{z - w}dz = \frac{1}{2\pi i}\int_{\partial\Omega} \frac{f(z)}{z - w}dz - f(w). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bbd3fec95a62c46d431eaf75e172d62b_l3.png)
- 对任意
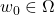 ,我们有
,我们有
因此,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} f(w) &= \frac{1}{2\pi i}\int_{\partial\Omega} \frac{1}{z - w_0}\frac{f(z)}{1 - \frac{w - w_0}{z - w_0}}dz \\ &= \sum_{n = 0}^\infty \bigg[\frac{1}{2\pi i}\int_{\partial\Omega} \frac{f(z)}{(z - w_0)^{n + 1}}dz\bigg] \cdot (w - w_0)^n. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1c047965286e1981579435d2bd292f17_l3.png)
 在
在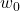 附近是解析的
附近是解析的
- Cauchy积分公式有一个奇点
- (开映射定理)复数域和实数域的第二个不同点,在于非常数的全纯函数一定为开映射。关键在于,全纯函数的退化情形类似于
 次函数,这是实数域不具备的良好性质
次函数,这是实数域不具备的良好性质
- (全纯同胚,非退化情形)当
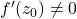 时,将
时,将 视为
视为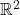 上的映射
上的映射![Rendered by QuickLaTeX.com \[ (x, y) \mapsto (u, v). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-10c518a4b039a48a41d858b66c08e708_l3.png)
- 由Cauchy-Riemann方程,Jacobi矩阵的行列式为
![Rendered by QuickLaTeX.com \[ \det\begin{bmatrix}\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y}\end{bmatrix} = \bigg(\frac{\partial u}{\partial x}\bigg)^2 + \bigg(\frac{\partial v}{\partial x}\bigg)^2 = |f'(z_0)|^2 \neq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dd9d0676e3fc1045fe75ac6aa5f72460_l3.png)
- 在
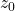 附近,由从切空间到局部中的逆映射定理,
附近,由从切空间到局部中的逆映射定理, 将开集映射到开集,故
将开集映射到开集,故 为开映射;由反函数的求导法则,
为开映射;由反函数的求导法则,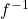 为全纯映射,故
为全纯映射,故 为全纯同胚
为全纯同胚
- 由Cauchy-Riemann方程,Jacobi矩阵的行列式为
- (分歧覆盖映射,退化情形)当
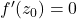 时,
时, 类似于
类似于 次函数
次函数
- 考虑
 次函数
次函数![Rendered by QuickLaTeX.com \[ P_n(z) = z^n,\; n \geq 2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-576fcde051c7d936e88e1f5def46bcbb_l3.png)
- 在
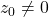 附近,它可以使用逆映射定理,所以是开映射,并且它的逆——开
附近,它可以使用逆映射定理,所以是开映射,并且它的逆——开 次方根函数为全纯函数。在
次方根函数为全纯函数。在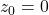 附近,它将模长
附近,它将模长 变为
变为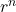 ,将幅角
,将幅角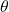 变为
变为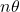 ,所以也是开映射
,所以也是开映射 - 在
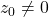 上,它将
上,它将 个不同点映射到一个点,所以是
个不同点映射到一个点,所以是 重覆盖映射。在
重覆盖映射。在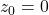 上,它将
上,它将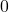 单独映射到
单独映射到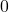 ,所以
,所以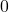 是一个分歧点。因此,
是一个分歧点。因此,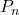 称为分歧覆盖映射,分歧点
称为分歧覆盖映射,分歧点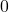 的重数为
的重数为
- 在
- 取一个平移,使得
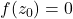 。由于
。由于 为非常数的解析函数,故存在解析函数
为非常数的解析函数,故存在解析函数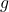 ,使得
,使得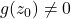 ,并且
,并且![Rendered by QuickLaTeX.com \[ f(z) = (z - z_0)^ng(z),\; n \geq 2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2e5dc60f8c8deb991c7d99a0ce32010e_l3.png)
- 令
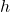 为
为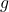 的开
的开 次方根,
次方根,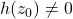 。那么,
。那么, 为一个全纯同胚,复合一个
为一个全纯同胚,复合一个 次函数,
次函数,
在![Rendered by QuickLaTeX.com \[ f: z \mapsto (z - z_0)h(z) \mapsto [(z - z_0)h(z)]^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f19ef77b447dc952dece4d0e91fa43a2_l3.png)
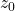 附近,
附近, 为开映射,并且
为开映射,并且 为分歧覆盖映射,分歧点
为分歧覆盖映射,分歧点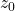 的重数为
的重数为
- 考虑
- (全纯同胚,非退化情形)当
复流形和代数基本定理
- 在从局部到整体中,
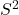 为2维
为2维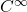 流形。在这里,
流形。在这里,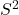 为1维复流形
为1维复流形
- (球极投影)
- 复数域和实数域的第三个不同点,在于复数域为代数封闭的域