二进制、逻辑和Boole代数

参考资料：Introduction to Boolean Algebras

软件和硬件

从二进制、逻辑到数字电子计算机
- 由从初等数论到交换代数、算术几何可知，Leibniz建立的二进制源于单子论（Monadology），而单子论受到了《易经》等中国哲学的启发
- 由从剑桥到哥廷根可知，Russell、Whitehead编写的Principia Mathematica，希望实现Leibniz的梦想，将数学建立在逻辑的基础之上，并且Wiener受到Russell的指导
- 由赛博理论的起点在清华大学？可知，基于在清华与李郁荣和顾毓琇的合作研究成果，Wiener给罗斯福总统的科学顾问Bush写信，正式提出二进制数字电子计算机（Binary Digital Electronic Computer）的设计原则，他们是麻省理工学院的先驱；在硅谷，我们有晶体管（Shockley） –> 集成电路（Noyce） –> 芯片（Intel） –> “家酿”计算机俱乐部（Apple）
数字电子计算机
- （软件）编程语言 –> 二进制，可参见编程语言的中间表示、从汇编指令到二进制
- （硬件）硬件描述语言 –> 逻辑门，可参见Verilog和数字电路、从数字电路到CPU
- 二进制、逻辑门具有相同的基础——Boole代数。因此，软件和硬件是等价的
  - 我们既可以用编程语言来编写软件，也可以用硬件描述语言来编写硬件
  - 在计算机图形学的重心坐标中，光线追踪的Möller–Trumbore相交算法既可以用CUDA实现，也可以用Verilog实现。前者是软实现，可以运行在GPU的CUDA核心上；后者是硬实现，可以固化为GPU的光线追踪核心
我们通常说的IT（Information Technology，信息技术）主要有两部分
- 计算机，即信息处理，可参见计算和信息
- 通信，即信息传输，可参见网络的随机模型
- 二者的结合，演化为Internet，可参见计算机网络架构
  - 计算机部分无论是有线端口（比如以太网口），还是无线端口（比如无线网卡），物理层都是半导体
  - 通信部分无论是有线传输（比如光纤），还是无线传输（比如蜂窝网络），物理层都是电磁波
- 计算机部分是数字的，通信部分是模拟的，二者的结合即硅——光、数——模。数字（离散）信号、模拟（连续）信号的基础为信息理论，可参见信噪比和位深

Boole代数

Boole代数是 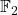$\mathbb{F}_2$ -代数，它和信息理论可以用来描述二进制编码，可参见一般线性编码
设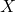为集合
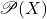- 幂集 $\mathscr{P}(X)$ 构成一个Boole代数 –> 幂集代数
- 映射集 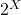$2^X$ 构成一个Boole环 –> Boole值函数的 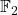$\mathbb{F}_2$ -代数