单位制
- 关于Maxwell方程组,可参见Maxwell方程组
- 在Gauss单位制下,Maxwell方程组为
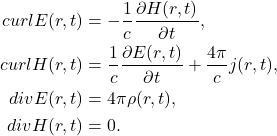
- 在国际单位制下,Maxwell方程组为
其中,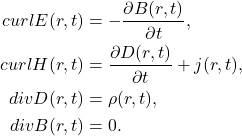
并且![Rendered by QuickLaTeX.com \[ D = \epsilon E,\; B = \mu H, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a4ac680771d04897e19173271cb8bc6c_l3.png)
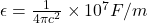 、
、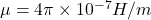 分别为电、磁常数
分别为电、磁常数 - 从Gauss单位制转换到国际单位制,可以使用如下变换
注意,![Rendered by QuickLaTeX.com \[ \rho \mapsto \frac{1}{\sqrt{4\pi\epsilon}}\rho,\; j \mapsto \frac{1}{\sqrt{4\pi\epsilon}}j,\; E \mapsto \sqrt{4\pi\epsilon}E,\; H \mapsto \sqrt{4\pi\mu}H. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9fa6667f5d4d119935995a63226dc103_l3.png)
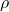 、
、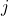 并不是独立的,它们需要满足电荷守恒定律
并不是独立的,它们需要满足电荷守恒定律![Rendered by QuickLaTeX.com \[ \frac{\partial\rho(r, t)}{\partial t} + divj(r, t) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b737c3ccf44ecbe2839590bc30eaf35f_l3.png)
射频的电磁波
- 在天线理论中,我们考虑射频。因为射频的带宽很窄,所以我们假设只有单一频率
从而,![Rendered by QuickLaTeX.com \[ E(r, t) = Re(E(r)e^{j\omega t}),\; H(r, t) = Re(H(r)e^{j\omega t}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a983ce2e09bb9c5f2136e02eafdc028a_l3.png)
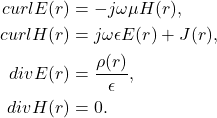
- 由于
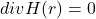 ,故存在磁势
,故存在磁势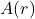 满足
满足
由于![Rendered by QuickLaTeX.com \[ curlA(r) = \mu H(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-becc781f7cda8bcb403c666e088612a8_l3.png)
![Rendered by QuickLaTeX.com curl[E(r) + j\omega A(r)] = 0](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-54d76fa44ea6484e00215c67eb83f830_l3.png) ,故存在电势
,故存在电势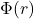 满足
满足![Rendered by QuickLaTeX.com \[ E(r) + j\omega A(r) = -\nabla\Phi(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ddc4beaa173c990363b06e1bfd2c9faa_l3.png)
- 接下来只需求解
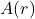 、
、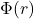 。我们剩下
。我们剩下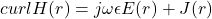 可以使用,其中
可以使用,其中
因此,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} curlH(r) &= \frac 1\mu curl\,curlA(r) \\ &= \frac 1\mu\nabla divA(r) - \frac 1\mu\Delta A(r), \\ j\omega\epsilon E(r) + J(r) &= j\omega\epsilon[-j\omega A(r) - \nabla\Phi(r)] + J(r) \\ &= \omega^2\epsilon A(r) - j\omega\epsilon\nabla\Phi(r) + J(r). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d9c3f4333ee5847fecd09049e3e8da0b_l3.png)
![Rendered by QuickLaTeX.com \[ \Delta A(r) + \omega^2\epsilon\mu A(r) - \nabla(j\omega\epsilon\mu\Phi(r) + divA(r)) + \mu J(r) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c471a1c852a87228ecb62b5175bcf07e_l3.png)
- 如下的规范变换将解变为解,
其中![Rendered by QuickLaTeX.com \[ A(r) \mapsto A(r) + \nabla\chi(r),\; \Phi(r) \mapsto \Phi(r) - \chi(r), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e6b9ebfa986b4ce58fe01682717cd8ed_l3.png)
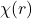 为任意函数。我们取Lorentz规范
为任意函数。我们取Lorentz规范
从而,![Rendered by QuickLaTeX.com \[ j\omega\epsilon\mu\Phi(r) + divA(r) = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-99d366c17f3d9947d00020eea0ecb075_l3.png)
![Rendered by QuickLaTeX.com \[ \Delta A(r) + \omega^2\epsilon\mu A(r) + \mu J(r) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6265557220c9b839d16ccf80c8081b43_l3.png)
求解非齐次Helmholtz方程
- 关于齐次Helmholtz方程,可参见量子化的物质波
- 在Lorentz规范下,由
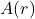 可以得到
可以得到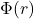 ,故我们只需求解
,故我们只需求解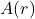 即可。
即可。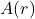 满足非齐次Helmholtz方程
满足非齐次Helmholtz方程
由使用Fourier变换求解PDE可知,我们可以先得到基本解![Rendered by QuickLaTeX.com \[ \Delta A(r) + \omega^2\epsilon\mu A(r) = -\mu J(r). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6973e1bcab5f380465b9f5e279536708_l3.png)
然后再使用卷积即可![Rendered by QuickLaTeX.com \[ \Delta\Gamma(r) + \omega^2\epsilon\mu\Gamma(r) = \delta(r), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-16af84f6eb2ce9253f14fd173dfa5946_l3.png)
- 利用Fourier变换,
其中,![Rendered by QuickLaTeX.com \[ (-4\pi^2|\xi|^2 + \beta^2)\widehat{\Gamma}(\xi) = 1, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cf868df6768eac3600ed341c8bcd2f19_l3.png)
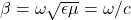 。那么
。那么![Rendered by QuickLaTeX.com \[ \Gamma = \bigg(\frac{1}{-4\pi^2|\xi|^2 + \beta^2}\bigg)^{\vee}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a054670caf3ca1621f30e5bc5d904133_l3.png)
- 这里的Fourier逆变换,不像使用Fourier变换求解PDE中求Laplace算子的基本解那样,可以利用伸缩性;不过,我们可以利用旋转性。令
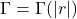 ,那么
,那么![Rendered by QuickLaTeX.com \[ 0 = \Delta\Gamma + \beta^2\Gamma = \frac{d^2\Gamma}{d|r|^2} + \frac{2}{|r|}\frac{d\Gamma}{d|r|} + \beta^2\Gamma,\; r \neq 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-667f6828190539c1d35b658b83daf3ef_l3.png)
因此,我们可以得到两个线性无关的基本解![Rendered by QuickLaTeX.com \[ (|r|\Gamma)'' + \beta^2(|r|\Gamma) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-59743a0900fec04295be858274cb7447_l3.png)
这里,出现常数![Rendered by QuickLaTeX.com \[ \frac{e^{-j\beta|r|}}{-4\pi|r|},\; \frac{e^{j\beta|r|}}{-4\pi|r|}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d5ee6ec00141e8cc6a60e1f9c472b8d5_l3.png)
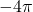 的原因是,当
的原因是,当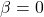 时,上述解应该等于Laplace算子在
时,上述解应该等于Laplace算子在 上的基本解
上的基本解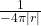
- 在天线理论中,我们考虑电磁波向外传播。按照量子化的物质波中传播方向的分析方法,我们取指数函数中符号为负的基本解。最终,使用卷积可得
![Rendered by QuickLaTeX.com \[ A(r) = \int \frac{e^{-j\beta|r - r'|}}{4\pi|r - r'|}\mu J(r')dV'. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-52954565a66ea245efaa0b256ae1a9e4_l3.png)