参考资料:信号与系统
时频分析
- 关于Fourier级数,可参见Fourier级数的收敛性。关于Fourier变换,可参见Fourier变换的反演公式
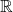 上的Fourier变换、Fourier逆变换为
上的Fourier变换、Fourier逆变换为
这里,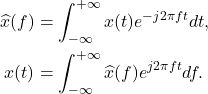
 为频率,单位为Hz,即
为频率,单位为Hz,即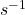
- 在时频分析中,我们通常使用角频率
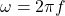 ,单位为
,单位为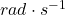 。此时,
。此时,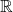 上的Fourier变换、Fourier逆变换为
上的Fourier变换、Fourier逆变换为
对于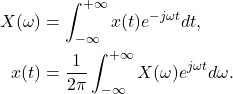
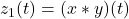 、
、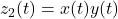 ,我们有
,我们有![Rendered by QuickLaTeX.com \[ Z_1(\omega) = X(\omega)Y(\omega),\; Z_2(\omega) = \frac{1}{2\pi}(X * Y)(\omega). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ac832715b9b676d7120a0e375e202c79_l3.png)
- 之所以称为时频分析,是因为
因此,![Rendered by QuickLaTeX.com \[ Ae^{j\omega_0t} = \int_{-\infty}^{+\infty} \delta(\omega - \omega_0)Ae^{j\omega t}d\omega = [2\pi A\delta(\omega - \omega_0)]^{\vee}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-589251a67a3c15a275e9c60ec33c9bdb_l3.png)
![Rendered by QuickLaTeX.com \[ (Ae^{j\omega_0t})^{\wedge} = 2\pi A\delta(\omega - \omega_0), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-70e1f0c71b96baa2395054a8cef51504_l3.png)
也就是说,指数信号、三角函数信号是时间上的信号,通过Fourier变换,我们可以提取出特定角频率![Rendered by QuickLaTeX.com \[ [A\cos(\omega_0t)]^{\wedge} = \frac A2(e^{j\omega_0t} + e^{-j\omega_0t})^{\wedge} = \pi A[\delta(\omega - \omega_0) + \delta(\omega + \omega_0)]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bffcf14143327dc14c4d138b7e17b01b_l3.png)
 的振幅
的振幅 。因此,
。因此, 称为频谱,关于时域
称为频谱,关于时域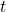 、频域
、频域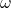 的分析称为时频分析
的分析称为时频分析 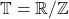 上的Fourier级数为
上的Fourier级数为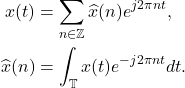
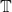 中的点为等价类,其中相差一个整数的点是等价的,所以
中的点为等价类,其中相差一个整数的点是等价的,所以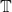 上的函数可以看成周期为1的函数
上的函数可以看成周期为1的函数- 令
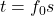 ,
,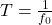 ,我们可以得到周期为
,我们可以得到周期为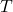 的Fourier级数
的Fourier级数
取角频率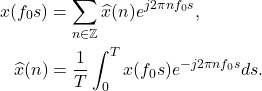
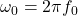 ,并且将
,并且将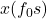 重命名为
重命名为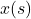 ,可得
,可得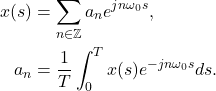
频率响应
- 系统是一个算子,它可以将输入信号
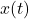 变为输出信号
变为输出信号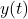 ,
,![Rendered by QuickLaTeX.com \[ F: x(t) \mapsto y(t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-239030f1d81347ee89a4e23fa9c0a8ff_l3.png)
- 如果
 为时不变的,那么
为时不变的,那么
其中,![Rendered by QuickLaTeX.com \[ \delta(t) \mapsto h(t),\; \delta(t - \tau) \mapsto h(t - \tau). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-20d2c271fb6878bdee60b29265a88ad2_l3.png)
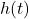 为脉冲信号
为脉冲信号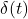 的系统响应
的系统响应 - 进一步,如果
 为线性的,那么
为线性的,那么
即![Rendered by QuickLaTeX.com \[ x(t) = \int_{-\infty}^{+\infty} x(\tau)\delta(t - \tau)d\tau \mapsto \int_{-\infty}^{+\infty} x(\tau)h(t - \tau)d\tau = y(t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-72fbd6185402489c3bc8ade2e7fd3f7b_l3.png)
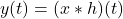 。利用Fourier变换,
。利用Fourier变换,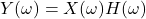 。也就是说,系统实际上是在信号的频谱
。也就是说,系统实际上是在信号的频谱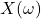 上乘以频率响应
上乘以频率响应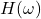
- 我们可以将
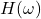 作为滤波器,改变频谱的形状。比如对于音频系统,我们可以
作为滤波器,改变频谱的形状。比如对于音频系统,我们可以
- 用一个带有二值开关的滤波器来决定是否削减低频
- 用一个带有连续开关的滤波器来调节中高频的增益
- 用一个前级放大器中的固定滤波器来补偿扬声器的频响特性
采样定理
- 我们用周期脉冲信号来采样,
其中,![Rendered by QuickLaTeX.com \[ p(t) = \sum_{n \in \mathbb{Z}} \delta(t - nT) = \sum_{n \in \mathbb{Z}} a_ne^{jn\omega_st}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f5e676762f640c0ad4201fe0c026601b_l3.png)
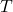 称为采样周期,
称为采样周期,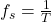 称为采样率,对应的角频率为
称为采样率,对应的角频率为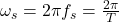
- 令
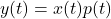 。利用Fourier变换,
。利用Fourier变换,
其中,![Rendered by QuickLaTeX.com \[ Y(\omega) = \frac{1}{2\pi}(X * P)(\omega). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fc10391696d5d596516b3dea54b5b9f2_l3.png)
因此,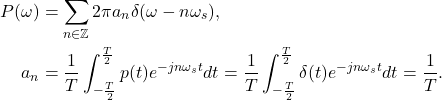
![Rendered by QuickLaTeX.com \[ Y(\omega) = \frac 1T\sum_{n \in \mathbb{Z}} X(\omega - n\omega_s). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e6dc4b30b818b082055eb1025128e973_l3.png)
- 采样相当于将信号的频谱平移
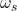 的整数倍,然后全部相加并乘以
的整数倍,然后全部相加并乘以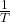 。如果
。如果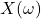 位于
位于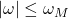 ,那么我们可以得到采样定理
,那么我们可以得到采样定理
- 当
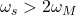 时,平移后的频谱不重叠,由样本可以恢复出原始信号
时,平移后的频谱不重叠,由样本可以恢复出原始信号 - 当
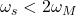 时,平移后的频谱重叠,由样本不可以恢复出原始信号
时,平移后的频谱重叠,由样本不可以恢复出原始信号 - 因此,信号最高频率的2倍为临界采样率,称为Nyquist采样率
- 当
- 比如对于CD格式,采样率为44.1kHz,而人能听到的频率范围为20Hz~20kHz。因此,CD格式可以恢复出人能听到的音乐
模拟信号的幅度调制
- 我们还可以将
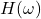 作为滤波器,选择特定范围的频率
作为滤波器,选择特定范围的频率 - 比如对于模拟信号的幅度调制,设基带信号为
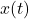 ,载波信号为
,载波信号为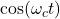 。那么,已调信号为
。那么,已调信号为
已调信号的频谱为![Rendered by QuickLaTeX.com \[ y(t) = x(t)\cos(\omega_ct), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ea4870d977f45a50a4225d88390fa64c_l3.png)
![Rendered by QuickLaTeX.com \[ Y(\omega) = \frac 12[X(\omega + \omega_c) + X(\omega - \omega_c)]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ea1402795f156deff6844124f913ce21_l3.png)
- 上面的调制方法相当于将频谱平移
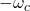 、
、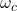 ,也就是复制了两份。为了减少带宽的占用,我们令已调信号的频谱为
,也就是复制了两份。为了减少带宽的占用,我们令已调信号的频谱为
已调信号为![Rendered by QuickLaTeX.com \[ Y(\omega) = \frac 12[X(\omega + \omega_c) + X(\omega - \omega_c)]H(\omega), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2c216db6dcf4c03ff199d0e9ff8f5e24_l3.png)
![Rendered by QuickLaTeX.com \[ y(t) = [x(t)\cos(\omega_ct)] * h(t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bc904c9afc3a9aaf0c40953aaed9a5f3_l3.png)
- 只保留上边带,对应于高通滤波器
![Rendered by QuickLaTeX.com \[ H(\omega) = \begin{cases} 1,\; & |\omega| > \omega_c, \\ 0,\; & |\omega| \leq \omega_c. \end{cases} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9d866c266dd78aba62091b035038b194_l3.png)
- 只保留下边带,对应于低通滤波器
![Rendered by QuickLaTeX.com \[ H(\omega) = \begin{cases} 1,\; & |\omega| \leq \omega_c, \\ 0,\; & |\omega| > \omega_c. \end{cases} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5fd7e36b69a9b619c81b01b29e2fe7c4_l3.png)
- 上面的滤波器在
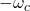 、
、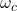 处突然截止,实际上无法实现,所以称为理想滤波器。一般地,我们考虑在
处突然截止,实际上无法实现,所以称为理想滤波器。一般地,我们考虑在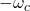 、
、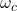 附近连续变化的滤波器,满足残留边带条件
附近连续变化的滤波器,满足残留边带条件![Rendered by QuickLaTeX.com \[ H(\omega + \omega_c) + H(\omega - \omega_c) = const. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a0415bea54cbb54c4094948c8b6d4e64_l3.png)
- 只保留上边带,对应于高通滤波器
- 解调方法
- 乘以
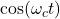 ,频谱变为
,频谱变为![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} &\mathrel{\phantom{=}} \frac 14X(\omega)[H(\omega + \omega_c) + H(\omega - \omega_c)] \\ &+ \frac 14[X(\omega + 2\omega_c)H(\omega + \omega_c) + X(\omega - 2\omega_c)H(\omega - \omega_c)]. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4c490b7f746202cf34cefe41900fbb33_l3.png)
- 经过一个低通滤波器,频谱变为
此时,我们已经可以恢复出原始信号![Rendered by QuickLaTeX.com \[ \frac 14X(\omega)[H(\omega + \omega_c) + H(\omega - \omega_c)] = const \cdot X(\omega). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e0c1bfbfe049d564fac162f7d8d8f956_l3.png)
- 乘以