参考资料:Spin Geometry
四元数和自旋群
- 模长为1的四元数
- 由四元数可知,模长为1的四元数可以视为3维球面
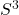 ,或者
,或者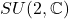
- 由计算机图形学的几何变换可知,模长为1的四元数
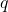 对应于
对应于 上的旋转
上的旋转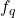 ,并且
,并且 上的旋转为
上的旋转为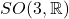 中的元素
中的元素
- 由四元数可知,模长为1的四元数可以视为3维球面
- 我们有群同态
![Rendered by QuickLaTeX.com \[ F: SU(2, \mathbb{C}) \to SO(3, \mathbb{R}),\; q \mapsto f_q. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-78ac0035cc6824b271b1fcf477c0de7f_l3.png)
- 根据计算机图形学的几何变换中的对应关系,
 为满的,故
为满的,故![Rendered by QuickLaTeX.com \[ SU(2, \mathbb{C}) / kerF \cong SO(3, \mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-368adb48a83f2b87301a2deb9f1a9089_l3.png)
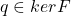 满足
满足
分别取![Rendered by QuickLaTeX.com \[ f_q(x) = x \Rightarrow qx = xq. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-144e2541fc4bbd6df6fc1a3bb5f0c188_l3.png)
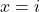 、
、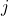 、
、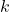 ,可得
,可得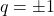
- 根据计算机图形学的几何变换中的对应关系,
 为二重覆盖映射
为二重覆盖映射
- 因为
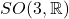 中的元素为
中的元素为 上的旋转(Rotation),所以
上的旋转(Rotation),所以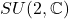 中的元素为
中的元素为 上的自旋(Spin),一个旋转对应于两个自旋
上的自旋(Spin),一个旋转对应于两个自旋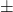
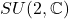 为自旋群,记为
为自旋群,记为![Rendered by QuickLaTeX.com \[ Spin(3) = SU(2, \mathbb{C}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e1fdce1de7c4e68e68fdda34e3bd95cb_l3.png)
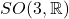 为3维实射影空间,
为3维实射影空间,
从而,![Rendered by QuickLaTeX.com \[ SO(3, \mathbb{R}) \cong S^3 / \{ \pm 1 \} \cong \mathbb{R}P^3. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7ffee252025702c8619d04b227873f1c_l3.png)
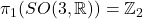
- 因为
- 一般的自旋群
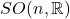 作用于
作用于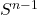 ,稳定子群为
,稳定子群为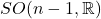 。令
。令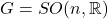 、
、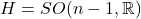 ,我们有纤维丛
,我们有纤维丛
利用同伦群的长正合列,![Rendered by QuickLaTeX.com \[ H \hookrightarrow G \to G / H \cong S^{n - 1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ffc1bd801a55d52aa56d8d8eec0a3d84_l3.png)
当![Rendered by QuickLaTeX.com \[ \pi_2(S^{n - 1}) \to \pi_1(SO(n - 1, \mathbb{R})) \to \pi_1(SO(n, \mathbb{R})) \to \pi_1(S^{n - 1}), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7b72ba530455c7f75b9424a0cf16f0f9_l3.png)
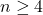 时,
时,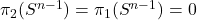 ,故
,故![Rendered by QuickLaTeX.com \[ \pi_1(SO(n, \mathbb{R})) \cong \pi_1(SO(n - 1, \mathbb{R})),\; n \geq 4. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a5445203458aff87c51ad2bfbc7a8f57_l3.png)
- 由上面的递推关系可知,
因此,![Rendered by QuickLaTeX.com \[ \pi_1(SO(n, \mathbb{R})) \cong \pi_1(SO(3, \mathbb{R})) = \mathbb{Z}_2,\; n \geq 4. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-62700453a10784d942a04d76b14435f8_l3.png)
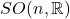 的二重万有覆盖空间为一个Lie群,称为自旋群,记为
的二重万有覆盖空间为一个Lie群,称为自旋群,记为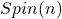
Clifford代数
- 自旋群,两种视角
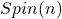 –>
–> 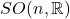 的二重万有覆盖空间
的二重万有覆盖空间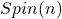 –> Clifford代数构造的Lie群
–> Clifford代数构造的Lie群
- Clifford代数和de Rham上同调群的定义中的外代数有关