Dirac符号
- 关于
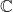 上的线性代数,可参见数值线性代数。关于
上的线性代数,可参见数值线性代数。关于 上的内积、Hermite形式,可参见矩阵群
上的内积、Hermite形式,可参见矩阵群 - 在量子力学中,我们使用如下Dirac符号(Dirac Notation)
- 数学期望、共轭、伴随算子
- 数学期望
![Rendered by QuickLaTeX.com \mathbb{E}[x]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8e52d514e3877630c05f88b26c3c5b05_l3.png) –>
–> 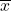
- 共轭
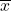 –>
–> 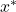
- 伴随算子
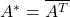 –>
–> 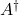
- 数学期望
- 单位正交基(右矢)、对偶单位正交基(左矢)
- 单位正交基
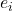 –> 右矢
–> 右矢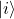
- 对偶单位正交基
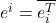 –> 左矢
–> 左矢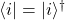
- 单位正交基
- 内积、Hermite形式
- 内积
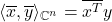 –>
–> 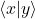
- Hermite形式
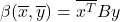 –>
–> 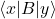
- 因此,在
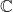 上的线性代数中,内积、Hermite形式关于第二个分量是共轭线性的;在量子力学中,内积、Hermite形式关于第一个分量是共轭线性的
上的线性代数中,内积、Hermite形式关于第二个分量是共轭线性的;在量子力学中,内积、Hermite形式关于第一个分量是共轭线性的
- 内积
- 数学期望、共轭、伴随算子
- 事实上,Dirac符号也适用于无限维、张量(泛函分析 + 张量分析),如下表所示
- 在无限维的情形下,我们无法取有限的基底;不过,我们仍然可以定义张量积,可参见模范畴和同态函子、张量积函子
- 张量积
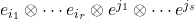 –>
–> 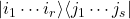
| 向量(函数) 矩阵(算子) | 张量 | |
| 有限维 | 线性代数 | 张量分析 |
| 无限维 | 泛函分析 | √ |