矩阵、行列式
- 求解线性方程
- 一元一次方程
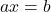 ,其解为
,其解为![Rendered by QuickLaTeX.com \[ x = a^{-1}b. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-63f6eae745f9674bda412979d3cd77df_l3.png)
- 二元一次方程组
根据系数的排列位置,记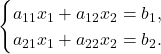
二元一次方程组![Rendered by QuickLaTeX.com \[ A = \begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix},\; B = \begin{bmatrix}b_1 \\ b_2\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-136e782e7cc17eb40609955ee6d93319_l3.png)
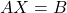 ,其解为
,其解为![Rendered by QuickLaTeX.com \[ X = A^{-1}B. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-16f1f7160becd693d30e8809cc0969f5_l3.png)
- 一元一次方程
- 我们需要定义什么是乘法
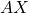 、什么是逆
、什么是逆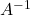
- 因为右边的系数
 为竖向排列的,所以我们令解
为竖向排列的,所以我们令解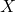 也为竖向排列的。从而,我们们可以得到乘法
也为竖向排列的。从而,我们们可以得到乘法
也就是说,乘法是左边的行,乘以右边的列。注意,乘法为结合的,但是为非交换的![Rendered by QuickLaTeX.com \[ \begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix} \cdot \begin{bmatrix}x_1 \\ x_2\end{bmatrix} = A \cdot X = AX = \begin{bmatrix}a_{11}x_1 + a_{12}x_2 \\ a_{21}x_1 + a_{22}x_2\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fd03d1fbcc3a99213fed72ade34e97b4_l3.png)
- 我们也可以直接求解方程组
- (消元过程)将第一式乘以
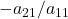 加到第二式,可以消去
加到第二式,可以消去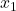 ,
,![Rendered by QuickLaTeX.com \[ \bigg(a_{22} - a_{12}\frac{a_{21}}{a_{11}}\bigg)x_2 = b_2 - b_1\frac{a_{21}}{a_{11}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4fc4889be15dac69971e909a7a8dda3b_l3.png)
- (代回过程)我们可以解得
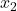 ,
,
将![Rendered by QuickLaTeX.com \[ x_2 = \frac{a_{11}b_2 - a_{21}b_1}{a_{11}a_{22} - a_{12}a_{21}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d47a054d957336feee2309a92fe88597_l3.png)
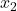 代回到第一式,我们可以解得
代回到第一式,我们可以解得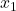 (由于下标1、2是对称的,故相当于1、2对换),
(由于下标1、2是对称的,故相当于1、2对换),![Rendered by QuickLaTeX.com \[ x_1 = \frac{a_{22}b_1 - a_{12}b_2}{a_{11}a_{22} - a_{12}a_{21}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f20cb23fce5186623fcad0f5faa40352_l3.png)
- (消元过程)将第一式乘以
- 从而,我们可以得到逆
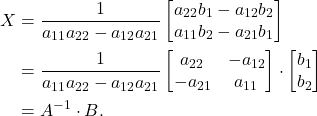
- 因为右边的系数
 、
、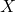 、
、 称为矩阵。因此,矩阵的乘法、逆可以用于求解方程组
称为矩阵。因此,矩阵的乘法、逆可以用于求解方程组
- 当
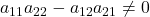 时,
时,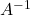 存在,
存在, 可逆,方程组有唯一解
可逆,方程组有唯一解 - 当
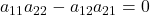 时,
时,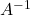 不存在,
不存在, 不可逆。不过,此时
不可逆。不过,此时 的两行系数只相差常数倍,如果
的两行系数只相差常数倍,如果 的两行系数相差同样的倍数,那么方程组有多于一个解,否则方程组无解
的两行系数相差同样的倍数,那么方程组有多于一个解,否则方程组无解 - 在第一种情形中,独立的方程为2个(非退化);在第二种情形中,独立的方程为1个或0个(退化)。因此,可逆即非退化,不可逆即退化
- 当
- 因为
 决定了
决定了 是否可逆,以及方程组解的个数,所以它称为决定式(Determinant),也叫做行列式,记为
是否可逆,以及方程组解的个数,所以它称为决定式(Determinant),也叫做行列式,记为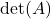 。同时,
。同时,
注意,![Rendered by QuickLaTeX.com \[ A^{-1} = \frac{1}{\det(A)}adj(A),\; adj(A) = \begin{bmatrix}a_{22} & -a_{12} \\ -a_{21} & a_{11}\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3e0a9093a3781acfe811d020b4afc985_l3.png)
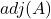 对应于伴随(Adjugate)矩阵,
对应于伴随(Adjugate)矩阵,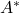 对应于伴随(Adjoint)算子,这里存在词语冲突,Adjugate、Adjoint是不同的
对应于伴随(Adjoint)算子,这里存在词语冲突,Adjugate、Adjoint是不同的
- Adjugate更接近于Conjugate(共轭),比如在四元数中,四元数的共轭对应于伴随矩阵
- Adjoint更常见,比如范畴论中的伴随函子
- 由于矩阵的逆满足
其中![Rendered by QuickLaTeX.com \[ A \cdot A^{-1} = A^{-1} \cdot A = I,\; I = \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-89601244f46f17e07faed07d43e95eee_l3.png)
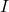 为单位矩阵,故伴随矩阵满足
为单位矩阵,故伴随矩阵满足![Rendered by QuickLaTeX.com \[ A \cdot adj(A) = adj(A) \cdot A = \det(A)I. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8b97697510b4b6964d173636c065bc44_l3.png)
Cramer法则、Gauss消元法
- 现在,我们将二元一次方程组推广到
 元一次方程组,即一般的线性方程。为了方便起见,我们考虑
元一次方程组,即一般的线性方程。为了方便起见,我们考虑 为可逆矩阵
为可逆矩阵
- Cramer法则
- 求解线性方程,等价于求矩阵的逆
- 求矩阵的逆,等价于求行列式、伴随矩阵
- 在一般情形下,伴随矩阵的系数全部为行列式。因此,线性方程的求解可以完全化归为行列式的计算,比如
![Rendered by QuickLaTeX.com \[ x_1 = \frac{\det\begin{bmatrix}b_1 & a_{12} \\ b_2 & a_{22}\end{bmatrix}}{\det\begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix}},\; x_2 = \frac{\det\begin{bmatrix}a_{11} & b_1 \\ a_{21} & b_2\end{bmatrix}}{\det\begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3411eadc87245792acad6d228bc41191_l3.png)
- Gauss消元法
- (消元过程)交换两行,使得第一行第一列不为零。将第一行乘以常数倍加到其他行,可以消去第一列的元。从第二行开始继续消元,直到倒数第一行只剩一个元
- (代回过程)解得倒数第一行的元,将其代回到其他行。从倒数第二行开始继续求解,直到解得全部元
- Cramer法则
- 由Cramer法则、Gauss消元法,可得一般情形下的行列式、伴随矩阵
- (Cramer法则)对于三元一次方程组,如果令第二、三行的
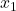 系数为0,那么
系数为0,那么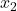 、
、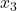 的方程组化归为二元一次方程组,比如
的方程组化归为二元一次方程组,比如
为了保持解是相同的,分子、分母应该相差相同的倍数![Rendered by QuickLaTeX.com \[ x_2 = \frac{\det\begin{bmatrix}a_{11} & b_1 & a_{13} \\ 0 & b_2 & a_{23} \\ 0 & b_3 & a_{33}\end{bmatrix}}{\det\begin{bmatrix}a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33}\end{bmatrix}} \Rightarrow x_2 = \frac{\det\begin{bmatrix}b_2 & a_{23} \\ b_3 & a_{33}\end{bmatrix}}{\det\begin{bmatrix}a_{22} & a_{23} \\ a_{32} & a_{33}\end{bmatrix}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2948b6a1b2ae49e40a929d742623d587_l3.png)
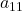 ,比如
,比如
因此,高阶行列式可以展开为低阶行列式![Rendered by QuickLaTeX.com \[ \det\begin{bmatrix}a_{11} & b_1 & a_{13} \\ 0 & b_2 & a_{23} \\ 0 & b_3 & a_{33}\end{bmatrix} = a_{11}\det\begin{bmatrix}b_2 & a_{23} \\ b_3 & a_{33}\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8eef93ce5e80b55cc6228fad1009e201_l3.png)
- (Gauss消元法)考虑如下三种运算,它们对应于三种初等矩阵。注意,它们对应于行列式的反对称性、线性
- (反对称性)交换两行,比如
![Rendered by QuickLaTeX.com \[ C = \begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix},\; A = \begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix},\; CA = \begin{bmatrix}a_{21} & a_{22} \\ a_{11} & a_{12}\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e184ab35c37814bdbd3188e4b4140337_l3.png)
- (线性,系数)某一行乘以常数倍,比如
![Rendered by QuickLaTeX.com \[ C = \begin{bmatrix}c & 0 \\ 0 & 1\end{bmatrix},\; A = \begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix},\; CA = \begin{bmatrix}ca_{11} & ca_{12} \\ a_{21} & a_{22}\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c9230dd2b0adfa5aed20b00676f8eb43_l3.png)
- (线性,加法)某一行加到另一行,比如
![Rendered by QuickLaTeX.com \[ C = \begin{bmatrix}1 & 1 \\ 0 & 1\end{bmatrix},\; A = \begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{bmatrix},\; CA = \begin{bmatrix}a_{11} + a_{21} & a_{12} + a_{22} \\ a_{21} & a_{22}\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f5e10ea998c9409e80cc117686c79fa1_l3.png)
- 对于初等矩阵
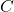 ,我们有
,我们有
对于一般的矩阵![Rendered by QuickLaTeX.com \[ \det(CA) = \det(C)\det(A). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f5d8957c95f0cbb44e8044bd85903ee2_l3.png)
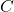 ,这个等式也成立
,这个等式也成立
- 当
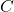 可逆时,由于三种运算求解线性方程,等价于三种初等矩阵生成
可逆时,由于三种运算求解线性方程,等价于三种初等矩阵生成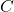 ,故等式成立
,故等式成立 - 当
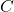 不可逆时,
不可逆时, 也不可逆,相应的行列式为0,故等式成立
也不可逆,相应的行列式为0,故等式成立
- 当
- (反对称性)交换两行,比如
- 高阶行列式可以展开为低阶行列式,并且行列式具有反对称性,故
 阶行列式为
阶行列式为![Rendered by QuickLaTeX.com \[ \det(A) = (-1)^0a_{11}M_{11} + \cdots + (-1)^{n - 1}a_{1n}M_{1n}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ea59de0a50f3b1915b6808288a1c3a87_l3.png)
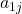 为第
为第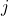 列对换到第1列(
列对换到第1列(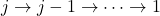 )后展开的系数,所以需要乘以
)后展开的系数,所以需要乘以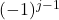 。
。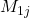 为
为 去掉第1行、第
去掉第1行、第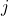 列后的行列式
列后的行列式- 一般地,
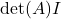 可以表示为
可以表示为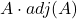 ,也可以表示为
,也可以表示为
因此,伴随矩阵为右边的矩阵,它的系数全部为行列式![Rendered by QuickLaTeX.com \[ \begin{bmatrix}a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{nn}\end{bmatrix} \cdot \begin{bmatrix}(-1)^{1 + 1}M_{11} & \cdots & (-1)^{1 + n}M_{n1} \\ \vdots & & \vdots \\ (-1)^{n + 1}M_{1n} & \cdots & (-1)^{n + n}M_{nn}\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a9bcb9760ae4a87817c8bafeeee26387_l3.png)
- 高阶行列式每展开一次就下降一阶,并且行、列下标
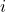 、
、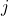 被去掉。如果将其完全展开为
被去掉。如果将其完全展开为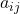 ,那么行、列下标不能重复
,那么行、列下标不能重复
- 当行下标固定为1~n时,列下标为1~n的置换,再加上反对称性,故
 阶行列式为
阶行列式为
其中,![Rendered by QuickLaTeX.com \[ \det(A) = \sum_{\sigma \in S_n} sign(\sigma) \cdot a_{1\sigma(1)} \cdots a_{n\sigma(n)}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-03f5e03f73e75f2aed8cf972f1a9ddcd_l3.png)
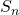 为
为 元置换群。当置换
元置换群。当置换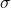 为偶数个对换时,
为偶数个对换时,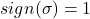 ;当置换
;当置换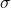 为奇数个对换时,
为奇数个对换时,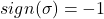
- 我们既可以固定行下标,也可以固定列下标,所以行列式关于行、列是对称的。取
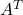 的第
的第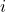 行等于
行等于 的第
的第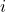 列,它称为
列,它称为 的转置,满足
的转置,满足![Rendered by QuickLaTeX.com \[ \det(A^T) = \det(A). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a0f811558d101786c0eeb8f3b4aa8899_l3.png)
- 当行下标固定为1~n时,列下标为1~n的置换,再加上反对称性,故
- (Cramer法则)对于三元一次方程组,如果令第二、三行的
- 上面,我们可以由行列式的性质,得到行列式的表达式。反过来,我们也可以由行列式的表达式,以及de Rham上同调群的定义中的外代数,直接导出行列式的所有性质
线性方程的求解,数值计算
- 尽管线性方程的求解可以完全化归为行列式的计算,并且行列式可以完全展开为
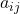 ,然而
,然而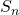 的阶为
的阶为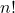 ,计算复杂度太高。因此,线性方程的求解通常基于Gauss消元法
,计算复杂度太高。因此,线性方程的求解通常基于Gauss消元法
- // 消元过程(Gaussian Elimination,GE)
- function
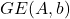
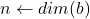
- for
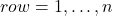
- for
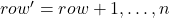
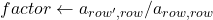
- for
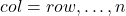

- for
- return
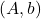
- // 代回过程(Backward Substitution,BS)
- function
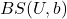
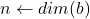
- for
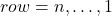
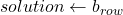
- for
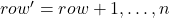
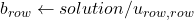
- return

- 在数值计算中,我们通常使用浮点数。因此,Gauss消元法的矩阵为浮点数矩阵
- 在一般情形下,浮点数等于0是不会成立的。为了方便起见,我们省略了交换两行的运算
- Gauss消元法的计算复杂度可以用浮点运算次数(Floating-Point Operations,flops)来表示,包括加法、减法、乘法、除法等。比如,消元过程为
代回过程为![Rendered by QuickLaTeX.com \[ \sum_{i = 1}^n\sum_{j = i + 1}^n [2(n - i + 1) + 3] \sim \sum_{i = 1}^n 2(n - i)^2 \sim \frac 23n^3\, (flops), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-32c6ce21e9d0e4709cf8dad7c857a0ec_l3.png)
因此,Gauss消元法的计算复杂度为![Rendered by QuickLaTeX.com \[ \sum_{i = 1}^n [2(n - i) + 1] \sim \sum_{i = 1}^n 2(n - i) \sim n^2\, (flops). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-52c0178289a3768287d6158b88351706_l3.png)
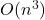
- 消元过程完成后,矩阵
 作为上三角矩阵
作为上三角矩阵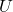 传入代回过程。如果将消元过程的所有
传入代回过程。如果将消元过程的所有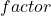 作为下三角矩阵
作为下三角矩阵 ,并且
,并且 的对角线为1,那么我们可以得到LU分解
的对角线为1,那么我们可以得到LU分解![Rendered by QuickLaTeX.com \[ A = LU. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b51c79919a787a6aa69536d8f277205a_l3.png)