Jordan闭曲线定理

概述

分离性
- 在1维情形，我们有Jordan闭曲线定理。 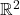$\mathbb{R}^2$ 中嵌入的1维圆环 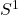$S^1$ 将其分为2个连通分支
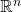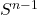- 在高维情形，我们有Jordan-Brouwer分离定理。 $\mathbb{R}^n$ 中嵌入的 $n - 1$ 维球面 $S^{n - 1}$ 将其分为2个连通分支
在2个连通分支中，一个为有界的，称为内部；另一个为无界的，称为外部
- 在1维情形，Schönflies定理成立。内部为2维球 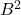$B^2$ ，外部为 $\mathbb{R}^2 - B^2$
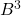- 在高维情形，Schönflies定理不成立。比如我们有 $\mathbb{R}^3$ 中嵌入的2维Alexander带角球面（Alexander Horned Sphere），内部为3维球 $B^3$ ，外部不是单连通的，所以不是 $\mathbb{R}^3 - B^3$
- 2维Alexander带角球面和扭结（Knot）、链环（Link）有关。 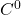$C^0$ 嵌入可能是狂野的（Wild），PL、 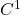$C^1$ 嵌入则是驯服的（Tame）。因此，Schönflies定理对于PL、 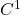$C^1$ 嵌入成立

2维Alexander带角球面，无限的角

由三角剖分的算法可知，多边形存在三角剖分
- 当三角形数量为1时，它的边界同胚于 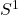$S^1$ ，它的内部同胚于 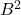$B^2$ ，它的外部同胚于 $\mathbb{R}^2 - B^2$
- 当三角形数量为2时，2个三角形沿着一条边粘贴在一起，相当于两个 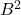$B^2$ 沿着边界的一条弧粘贴在一起。因此，在同胚的意义下，它的边界、内部、外部仍然和上面一样
- 对多边形的三角形数量使用数学归纳法，Jordan闭曲线定理、Schönflies定理成立
接下来，类似于Jordan’s Proof of the Jordan Curve Theorem中的方法，我们将Jordan闭曲线化归为多边形