度量
- 设
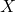 为集合。
为集合。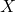 上的度量(Metric),或者距离(Distance)为
上的度量(Metric),或者距离(Distance)为
它满足如下条件![Rendered by QuickLaTeX.com \[ d: X \times X \to \mathbb{R} \cup \{ \infty \}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9c5463c017cec63dd1893cad286f5fd1_l3.png)
- (自反性)
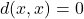
- (对称性)
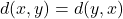
- (传递性)
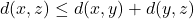
- (正定性)
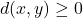 ,并且
,并且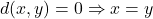
- (自反性)
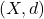 称为度量空间(Metric Space),或者距离空间(Distance Space)
称为度量空间(Metric Space),或者距离空间(Distance Space)
- 如果
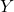 为
为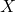 的子集,那么
的子集,那么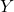 上的子空间度量为
上的子空间度量为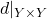
- 由定义可知,我们有如下的等价关系
也就是说,![Rendered by QuickLaTeX.com \[ x \sim y \text{ for any } d(x, y) < \infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fafc658b67c83a19d1aab658b9a0fc67_l3.png)
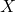 可以分解为子集的不交并,同一子集之间的两点距离有限,不同子集之间的两点距离无限。因此,我们也可以化归为距离有限的情形
可以分解为子集的不交并,同一子集之间的两点距离有限,不同子集之间的两点距离无限。因此,我们也可以化归为距离有限的情形 - 注意,度量是有限的度量,Riemann度量是无穷小的度量,二者是不同的。正如无穷小旋转可以生成有限旋转,Riemann度量也可以生成度量
- 如果
- 度量的性质
- 传递性是主要性质,它也叫做三角不等式(在三角形中,两边之和大于第三边)
- 正定性对应于内积,所以度量可以由内积诱导
- 在度量空间中,我们可以定义收敛、极限(根据三角不等式,极限唯一),
从而,我们可以定义Cauchy列,![Rendered by QuickLaTeX.com \[ x_n \to x \Leftrightarrow d(x_n, x) \to 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cbe872f9bc28b8d860dcc7c89ffb493f_l3.png)
如果Cauchy列收敛,那么![Rendered by QuickLaTeX.com \[ x_n \text{ is a Cauchy sequence} \Leftrightarrow d(x_m, x_n) \to 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-15f926d26ab35add9ff86519735a2b48_l3.png)
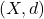 称为完备度量空间
称为完备度量空间
泛函分析中的空间
- 关于
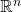 、
、 上的内积、范数,可参见矩阵群
上的内积、范数,可参见矩阵群 - 在
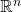 上的内积为
上的内积为
它是对称、正定的双线性形式。注意,正定性需要使用全序关系,所以对于一般的域上的线性空间,内积的定义是不同的![Rendered by QuickLaTeX.com \[ \langle{x, y}\rangle_{\mathbb{R}^d} = x^Ty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-04cc24491525822cebba1a41fc0d5d1b_l3.png)
- 复数域 –> 需要使用线性-共轭线性形式
- 一般的域 –> 需要去掉正定性,比如一般线性编码中的内积
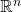 上的内积、范数分别为
上的内积、范数分别为
它诱导Euclid度量![Rendered by QuickLaTeX.com \[ \langle{x, y}\rangle_{\mathbb{R}^d} = x^Ty,\; ||x|| = \sqrt{\langle{x, x}\rangle_{\mathbb{R}^n}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-01992b230ff39305405e0942bc142aa2_l3.png)
![Rendered by QuickLaTeX.com \[ d(x, y) = ||x - y||. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-97eddc159b8461a79b658a30534a279b_l3.png)
- 我们也可以取其他范数,比如
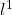 、
、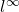 范数
范数
它们分别诱导![Rendered by QuickLaTeX.com \[ ||x||_1 = \sum_{i = 1}^n |x_i|,\; ||x||_\infty = \max_{1 \leq i \leq n} |x_i|. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-46617fa5306186ac7bc57124a80053c0_l3.png)
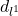 、
、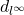
- 我们也可以取其他范数,比如
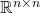 上的范数为
上的范数为
它诱导度量![Rendered by QuickLaTeX.com \[ ||A|| = \sup_{x \neq 0} \frac{||Ax||}{||x||} = \sup_{||x|| = 1} ||Ax||. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-71e7e6731480026488253e3efc870a0b_l3.png)
![Rendered by QuickLaTeX.com \[ d(A, B) = ||A - B||. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-45243bcf92a41233929be3163cf9e78a_l3.png)
- 由数值线性代数中的奇异值分解可知,
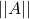 等于
等于 的最大奇异值
的最大奇异值
- 由数值线性代数中的奇异值分解可知,
- 由上述可知,内积可以诱导范数,范数可以诱导度量。因此,内积空间为带范数的线性空间,带范数的线性空间为度量空间
- Hilbert空间为完备的内积空间,Banach空间为完备的带范数的线性空间
- 矩阵还是带范数的
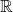 -代数,范数和乘法的相容性为
-代数,范数和乘法的相容性为
Banach代数为完备的带范数的![Rendered by QuickLaTeX.com \[ ||AB|| \leq ||A|| \cdot ||B||. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-98d67cbd87ed2928208b47007ee00057_l3.png)
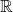 -代数
-代数
度量诱导的拓扑
- 进一步,度量可以诱导拓扑。因此,度量空间为拓扑空间
- 在度量空间
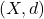 中,开球为
中,开球为
闭球为![Rendered by QuickLaTeX.com \[ B_r(x) = \{ y \in X : d(y, x) < r \}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-acf19e5632c89ba6e75974e2e01608f1_l3.png)
![Rendered by QuickLaTeX.com \[ \overline{B}_r(x) = \{ y \in X : d(y, x) \leq r \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0f460c509cf0f9bdb470bbca4f49f7be_l3.png)
- 在不同的度量空间中,开球、闭球是不同的
- 在Lebesgue测度中,我们有AABB(Axis-Aligned Bounding Box,沿坐标轴对齐的包围盒)。
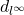 、
、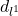 的开球分别对应于开的AABB、开的AABB作仿射变换
的开球分别对应于开的AABB、开的AABB作仿射变换 - 注意,开球的闭包不一定为闭球,比如一般线性编码中的
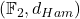
- 在Lebesgue测度中,我们有AABB(Axis-Aligned Bounding Box,沿坐标轴对齐的包围盒)。
- //
- 拓扑不一定是由度量诱导的,比如代数几何的Zariski拓扑
- Zariski拓扑可以建立在环的谱(Spectrum)上,以下三种谱是一致的
- 环的谱
- 算子的谱
- 光谱