磨光核
- 核函数和卷积的性质源于
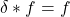
- 在Fourier级数的收敛性中,Dirichlet核
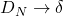 、Fejér核
、Fejér核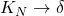 ,故
,故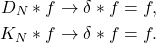
- 在Fourier变换的反演公式中,Gauss核
 ,故
,故![Rendered by QuickLaTeX.com \[ G_\epsilon * f \to \delta * f = f. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d1e5c4cf6bb4154f75e96201c8477603_l3.png)
- 在复数域上的分析中,Cauchy核与
 (在边界上)卷积之后为
(在边界上)卷积之后为 本身,这是通过Stokes定理,将区域上的卷积
本身,这是通过Stokes定理,将区域上的卷积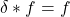 转化为边界上的卷积
转化为边界上的卷积
- 在Fourier级数的收敛性中,Dirichlet核
- 在这里,我们考虑磨光核
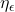 ,它不仅满足
,它不仅满足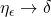 ,而且与非光滑的函数卷积之后可以得到光滑的函数,所以它也叫做光滑化子(Mollifier)
,而且与非光滑的函数卷积之后可以得到光滑的函数,所以它也叫做光滑化子(Mollifier)
- 由于
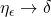 ,故
,故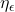 的积分为1(归一化),并且越来越集中于0附近(局部化)。又由于
的积分为1(归一化),并且越来越集中于0附近(局部化)。又由于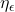 可以将非光滑的函数光滑化,故
可以将非光滑的函数光滑化,故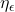 本身是光滑的
本身是光滑的 - 指数函数比多项式的增长更快,所以
考虑如下函数![Rendered by QuickLaTeX.com \[ P(x)e^{-x} \to 0 \text{ as } x \to +\infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ac8d4d63f4ccdf7fb881a7f4a269ccab_l3.png)
我们有![Rendered by QuickLaTeX.com \[ f(x) = \begin{cases}e^{-\frac 1x},\; & x > 0, \\ 0,\; & x \leq 0.\end{cases} \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c5f5f7abf33b1aaf243325cca88c3459_l3.png)
因此,![Rendered by QuickLaTeX.com \[ \frac{d^nf}{dx^n} = P\bigg(\frac 1x\bigg)e^{-\frac 1x} \to 0 \text{ as } x \to 0^+. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d6d615228aa26b95e9e636f24160b28a_l3.png)
 为
为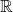 上的光滑函数。特别地,
上的光滑函数。特别地, 在0处是光滑的,但不是解析的——它在0处的Taylor展开式为0,但它在0附近不为0
在0处是光滑的,但不是解析的——它在0处的Taylor展开式为0,但它在0附近不为0 - 通过取范数,我们可以得到
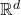 上的光滑函数
上的光滑函数
这里,![Rendered by QuickLaTeX.com \[ \eta(x) = f(1 - |x|^2),\; x \in \mathbb{R}^d. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cbded4a420bd4402623c543d31b332fc_l3.png)
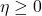 ,并且
,并且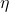 只在
只在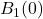 上非0。我们称
上非0。我们称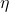 的支撑集为
的支撑集为
最后,利用伸缩,我们可以得到满足归一化、局部化的磨光核![Rendered by QuickLaTeX.com \[ supp(\eta) = \overline{\{ x \in \mathbb{R}^d : \eta(x) \neq 0 \}} = \overline{B_1(0)}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9ad78a342a887f16cb231e79bcf6080c_l3.png)
![Rendered by QuickLaTeX.com \[ \eta_\epsilon(x) = C \cdot \epsilon^{-d}\eta(\epsilon^{-1}x). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-05f00db610f22d305ee76a2e5e05c91a_l3.png)
- 由于