参考资料:偏微分方程
基本解和Green函数
- 求解Poisson方程
![Rendered by QuickLaTeX.com \[ \Delta u = f. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-21395958b03e676655edbe4d5640356a_l3.png)
- 我们可以先得到基本解
再使用卷积即可![Rendered by QuickLaTeX.com \[ \Delta\Gamma(x) = \delta(x), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a9577f481cdf30715302a9bd422b433d_l3.png)
![Rendered by QuickLaTeX.com \[ \Delta(\Gamma * f) = (\Delta\Gamma) * f = \delta * f = f. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8a3148200d72ffd60da8612d8c3e7053_l3.png)
- 或者,我们可以先得到Green函数
再使用积分变换即可![Rendered by QuickLaTeX.com \[ \Delta G(x, y) = \delta(x - y), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-01564f639fd22ae779f9d5ee38bfcd2a_l3.png)
![Rendered by QuickLaTeX.com \[ \Delta(G * f) = (\Delta G) * f = \delta * f = f. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0c088880442a84228b8b317e89f2fe96_l3.png)
- 我们可以先得到基本解
- 此方法可以将求解非齐次方程(右端为
 )基本上化归为求解齐次方程(右端为
)基本上化归为求解齐次方程(右端为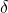 ),它不仅适用于Laplace算子
),它不仅适用于Laplace算子 ,也适用于常系数的微分算子
,也适用于常系数的微分算子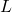 。进一步,求解齐次方程需要其他方法
。进一步,求解齐次方程需要其他方法
- 由Fourier变换的反演公式可知,Fourier变换可以将常系数的微分算子变为代数的乘法算子,所以我们可以先进行Fourier变换,求解变换后的方程,再进行Fourier逆变换,得到PDE的解
- 椭圆型(
 ) –> Laplace算子的基本解
) –> Laplace算子的基本解 - 抛物型(
 ) –> 热方程
) –> 热方程 - 色散型(
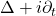 ) –> Schrödinger方程
) –> Schrödinger方程 - 双曲型(
 ) –> 弦振动方程
) –> 弦振动方程
- 椭圆型(
- 一般地,将代数的乘法算子,更换为一般的乘法算子,可得伪微分算子
- 由Fourier变换的反演公式可知,Fourier变换可以将常系数的微分算子变为代数的乘法算子,所以我们可以先进行Fourier变换,求解变换后的方程,再进行Fourier逆变换,得到PDE的解
求Laplace算子的基本解
- 关于Gamma函数
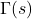 (和基本解的符号冲突),可参见Beta函数和Gamma函数
(和基本解的符号冲突),可参见Beta函数和Gamma函数 - 求Laplace算子在
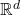 上的基本解
上的基本解![Rendered by QuickLaTeX.com \[ \Delta\Gamma(x) = \delta(x). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-afe5d09fcc2a75fcf9b718652695d03e_l3.png)
- 进行Fourier变换,
求解变换后的方程,再进行Fourier逆变换,![Rendered by QuickLaTeX.com \[ -4\pi^2|\xi|^2\widehat{\Gamma}(\xi) = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3845683f1f424a8c7671299d8ac6c2df_l3.png)
![Rendered by QuickLaTeX.com \[ \Gamma(x) = -\frac{1}{4\pi^2}(|\xi|^{-2})^{\vee}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ea483fb21adeebb3e6b14c061e1ed7d4_l3.png)
- 下面,我们计算一般的
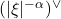 ,
,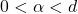 。利用
。利用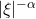 的伸缩性、旋转对称性,以及Fourier变换的反演公式中的伸缩性、旋转性,可得
的伸缩性、旋转对称性,以及Fourier变换的反演公式中的伸缩性、旋转性,可得
关键在于计算![Rendered by QuickLaTeX.com \[ (|\xi|^{-\alpha})^{\vee} = C|x|^{\alpha - d}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-20ce8c00ba859bb53edc50d238394c34_l3.png)
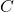 。受到Math StackExchange的启发,令
。受到Math StackExchange的启发,令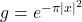 ,由Plancherel定理可知,
,由Plancherel定理可知,
分别计算左右两端,我们使用Gamma函数![Rendered by QuickLaTeX.com \[ \langle{C|x|^{\alpha - d}, g}\rangle_{L^2} = \langle{|\xi|^{-\alpha}, \widehat{g}}\rangle_{L^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9bb2ed217a1d9b526155c2ad8ead5804_l3.png)
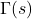 。左端为
。左端为
类似地,右端为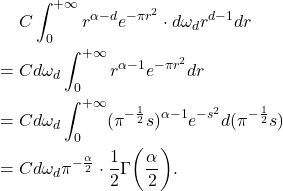
因此,![Rendered by QuickLaTeX.com \[ d\omega_d\pi^{-\frac{d - \alpha}{2}} \cdot \frac 12\Gamma\bigg(\frac{d - \alpha}{2}\bigg). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-98d1cebb1a8ecaeeac5d8f6d3531ce9a_l3.png)
![Rendered by QuickLaTeX.com \[ C = \pi^{\alpha - \frac d2}\frac{\Gamma(\frac{d - \alpha}{2})}{\Gamma(\frac{\alpha}{2})}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bbce341cd55a47d762a198487910edc8_l3.png)
- 当
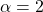 时,
时,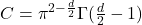 。利用
。利用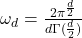 ,我们可以得到
,我们可以得到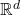 上的基本解,
上的基本解,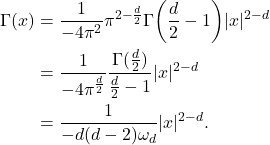
- 在Maxwell方程组中,我们使用了一个等式
这可以由Laplace算子在![Rendered by QuickLaTeX.com \[ \Delta\frac{1}{|r - r'|} = -4\pi\delta(r - r'). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-402a9e06c406e40f3e52035abed5b613_l3.png)
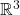 上的基本解得到,
上的基本解得到,![Rendered by QuickLaTeX.com \[ \Delta(|x|^{-1}) = -3\omega_3\Delta\Gamma(x) = -4\pi\delta(x). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-34d6cc426bbb63ce78a185869723db20_l3.png)
求解热方程
- 求解热方程
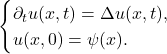
- 进行Fourier变换,
求解变换后的方程,再进行Fourier逆变换,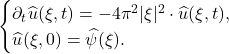
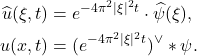
- 注意到
因此,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} (e^{-\pi|(4\pi t)^{\frac 12}\xi|^2})^{\vee}(x) &= (4\pi t)^{-\frac d2}(e^{-\pi|\xi|^2})^{\vee}\bigg[\frac{x}{(4\pi t)^{\frac 12}}\bigg] \\ &= (4\pi t)^{-\frac d2}e^{-\frac{|x|^2}{4t}}. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b757db7799bd76effbbd90f5b80bb73e_l3.png)
![Rendered by QuickLaTeX.com \[ u(x, t) = \int_{\mathbb{R}^d} (4\pi t)^{-\frac d2}e^{-\frac{|x - y|^2}{4t}}\psi(y)dy. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-52171e8d8a70a9ec9daa1de2a594ad67_l3.png)
求解Schrödinger方程
- 求解Schrödinger方程
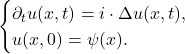
- 进行Fourier变换,
求解变换后的方程,再进行Fourier逆变换,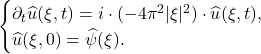
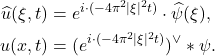
- 注意到
因此,![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} (e^{-\pi|(i \cdot 4\pi t)^{\frac 12}\xi|^2})^{\vee}(x) &= (i \cdot 4\pi t)^{-\frac d2}(e^{-\pi|\xi|^2})^{\vee}\bigg[\frac{x}{(i \cdot 4\pi t)^{\frac 12}}\bigg] \\ &= (i \cdot 4\pi t)^{-\frac d2}e^{i \cdot \frac{|x|^2}{4t}}. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6a82faa6a12c03e3fe96ca818b11650a_l3.png)
![Rendered by QuickLaTeX.com \[ u(x, t) = \int_{\mathbb{R}^d} (i \cdot4\pi t)^{-\frac d2}e^{i \cdot \frac{|x - y|^2}{4t}}\psi(y)dy. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-882b4c5f7520c5d4481a332ee28c2938_l3.png)
求解弦振动方程
- 弦振动是1维波动,水面波是2维波动,声波、电磁波是3维波动。在这里,我们考虑弦振动方程,即1维波动方程
![Rendered by QuickLaTeX.com \[ \partial_{tt}u(x, t) = \partial_{xx}u(x, t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-19a6f82bada289e23c5c8d1559c6e48c_l3.png)
- 进行Fourier变换,
求解变换后的方程,再进行Fourier逆变换,![Rendered by QuickLaTeX.com \[ \partial_{tt}\widehat{u}(\xi, t) = -4\pi^2\xi^2\widehat{u}(\xi, t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e244803480c8c84df7fd96b39d87e40e_l3.png)
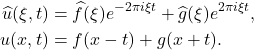
- 这里,
 、
、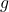 为任意函数,并且我们利用了Fourier变换的反演公式中的平移性。因此,1维波动可以分解为正向波、反向波,这称为d’Alembert公式
为任意函数,并且我们利用了Fourier变换的反演公式中的平移性。因此,1维波动可以分解为正向波、反向波,这称为d’Alembert公式