微分结构
- 微分结构是流形上的第一个整体结构。然而,流形上可能不存在微分结构,或者存在多个微分结构
- 对于2维、3维,流形上存在唯一的微分结构。我们需要利用流形上的三角剖分,首先得到PL(Piecewise Linear,分片线性)结构,然后得到微分结构
- 对于4维,我们可以用Seiberg-Witten不变量来研究流形上的微分结构
- 流形

- (局部坐标邻域)我们有开覆盖
![Rendered by QuickLaTeX.com \[ M = \cup_i U_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-770b165f1a5a5690b79c5299c5bbfaf9_l3.png)
- (局部坐标映射)我们有同胚,从
 的开集到
的开集到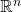 的开集
的开集![Rendered by QuickLaTeX.com \[ \varphi_i: U_i \subset M \to \varphi_i(U_i) \subset \mathbb{R}^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-df5dfdb3f18b1275735aff81cf9bdc50_l3.png)
- 流形在日语中叫做多様体(たようたい)。也就是说,流形是(在局部)可以用多维坐标来描述的形体,流形的维数为坐标的维数。进一步,如果要建立流形上的分析,以及更多的几何结构,那么我们还需要流形上的微分结构
- (局部坐标邻域)我们有开覆盖
- 流形
 上的
上的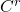 微分结构,
微分结构,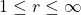
- (转移映射)我们有
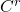 微分同胚,从
微分同胚,从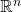 的开集到
的开集到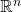 的开集
的开集![Rendered by QuickLaTeX.com \[ \varphi_j \circ \varphi_i^{-1}: \varphi_i(U_i \cap U_j) \subset \mathbb{R}^n \to \varphi_j(U_i \cap U_j) \subset \mathbb{R}^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c3b75ff7dd60dfa1a9f201bf7a11b6f2_l3.png)
- 转移映射自动为
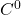 同胚。因此,流形也叫做
同胚。因此,流形也叫做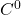 流形(或者拓扑流形)
流形(或者拓扑流形) - 进一步,如果转移映射为
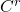 微分同胚,那么我们可以得到
微分同胚,那么我们可以得到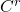 流形(或者微分流形);
流形(或者微分流形);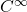 流形也叫做光滑流形
流形也叫做光滑流形 - 我们也可以考虑其他正则性。如果转移映射为
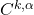 微分同胚,那么我们可以得到
微分同胚,那么我们可以得到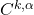 流形。注意,
流形。注意,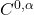 流形可能不存在一阶微分算子,从而不存在切空间;
流形可能不存在一阶微分算子,从而不存在切空间;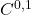 流形也叫做Lipschitz流形
流形也叫做Lipschitz流形
- (转移映射)我们有
- 下面,我们提升微分结构的正则性,从
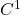 微分结构提升到
微分结构提升到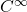 微分结构。然而,
微分结构。然而,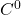 无法提升到
无法提升到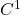 ,即拓扑流形和微分流形具有本质的不同
,即拓扑流形和微分流形具有本质的不同
- 在逆映射定理中,
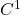 映射的局部性质可以通过Jacobi矩阵控制,而
映射的局部性质可以通过Jacobi矩阵控制,而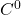 映射的局部性质则无法控制。因此,
映射的局部性质则无法控制。因此,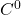 映射可能是病态的(Pathological),比如处处连续但处处不可微的映射
映射可能是病态的(Pathological),比如处处连续但处处不可微的映射
- 在逆映射定理中,
提升微分结构的正则性
- 使用PDE的解的正则性中的磨光核和卷积,提升正则性
丛、层
- 关于切丛、余切丛、张量丛,可参见纤维丛的定义
- 我们用农业来播种
 为集合
为集合
- 土地是裸露的岩石
 赋予拓扑,成为一个拓扑空间。进一步,
赋予拓扑,成为一个拓扑空间。进一步, 赋予局部坐标,成为一个流形
赋予局部坐标,成为一个流形
- 土地仍然贫瘠
 赋予
赋予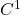 微分结构,成为一个微分流形。进一步,
微分结构,成为一个微分流形。进一步, 的
的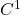 微分结构提升到
微分结构提升到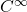 微分结构,成为一个光滑流形
微分结构,成为一个光滑流形
- 土地有了第一层土壤,并且经过改良,可以开始种植作物
 上的切丛为
上的切丛为![Rendered by QuickLaTeX.com \[ p: TM \to M. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-66d5b206b5485e5ebacd80b5452b2019_l3.png)
- 如果在一点
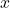 处收获,那么可以得到作物的纤维(Fiber)
处收获,那么可以得到作物的纤维(Fiber)![Rendered by QuickLaTeX.com \[ p^{-1}(x) \cong \mathbb{R}^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d432341a92c3c0de2fe33725bdc90673_l3.png)
- 如果在局部平凡化邻域
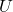 处收获,那么可以得到作物的丛(Bundle)
处收获,那么可以得到作物的丛(Bundle)![Rendered by QuickLaTeX.com \[ p^{-1}(U) \cong U \times \mathbb{R}^n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0b7e27795697b571fe5c8e3242c64a70_l3.png)
- 如果在一点
- 由纤维丛的定义可知,我们也可以观察截面。设
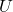 为开集,那么
为开集,那么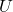 上的截面为
上的截面为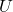 上的切向量场,
上的切向量场,![Rendered by QuickLaTeX.com \[ \mathcal{T}(U) = \{ s: U \to TM \text{ is a section} \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-35c1216b1712653b5f94b99870904f18_l3.png)
- 如果在一点
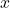 处收获,那么可以得到作物的茎(Stalk)
处收获,那么可以得到作物的茎(Stalk)![Rendered by QuickLaTeX.com \[ \mathcal{T}_x. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-10ac1d2257dcf46a5e66b7ecc88d91b6_l3.png)
- 如果在开集
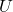 处收获,那么可以得到作物的捆(Sheaf)
处收获,那么可以得到作物的捆(Sheaf)![Rendered by QuickLaTeX.com \[ \mathcal{T}(U). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6fae69528e85d12053a3f65b7ce7b4dc_l3.png)
- 捆论(Sheaf Theory)也叫做层论,它研究土地上种植的不同品种之间的关系
- 如果在一点
- 流形上的几何结构通常是一个张量,比如双线性形式。通常,我们考虑双线性形式的矩阵
 为非退化的,它可以分解为一个对称部分,一个反对称部分
为非退化的,它可以分解为一个对称部分,一个反对称部分![Rendered by QuickLaTeX.com \[ B = \frac{B+ B^T}{2} + \frac{B - B^T}{2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bfec79517b4b52ec1a2ca7b1acf5e571_l3.png)
- 如果
 只有对称、正定的部分,那么我们可以得到Riemann流形,它对应于Riemann几何
只有对称、正定的部分,那么我们可以得到Riemann流形,它对应于Riemann几何 - 如果
 只有对称、不定的部分,那么我们可以得到伪Riemann流形,它对应于伪Riemann几何
只有对称、不定的部分,那么我们可以得到伪Riemann流形,它对应于伪Riemann几何 - 如果
 只有反对称的部分,那么我们可以得到辛流形,它对应于辛几何
只有反对称的部分,那么我们可以得到辛流形,它对应于辛几何
- 如果