Schwartz空间
- Schwartz空间为
![Rendered by QuickLaTeX.com \[ \mathcal{S}(\mathbb{R}^d) = \{ f \in C^\infty(\mathbb{R}^d) : x^\alpha\partial_x^\beta f(x) \in L^\infty(\mathbb{R}^d) \text{ for any } \alpha, \beta \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4e888bebd2c5d314b41bc18087fb7645_l3.png)
- 如果
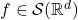 ,那么
,那么 的Fourier变换为
的Fourier变换为![Rendered by QuickLaTeX.com \[ \widehat{f}(\xi) = \int_{\mathbb{R}^d} e^{-2\pi ix \cdot \xi}f(x)dx,\; \xi \in \mathbb{R}^d. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4d8fd742db6a74736717b58b721789a6_l3.png)
- 由定义可知,
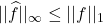
- (平移性)对任意
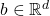 ,我们有
,我们有![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} [f(x + b)]^\wedge(\xi) &= \int_{\mathbb{R}^d} e^{-2\pi ix \cdot \xi}f(x + b)dx \\ &= \int_{\mathbb{R}^d} e^{-2\pi i(y - b) \cdot \xi}f(y)d(y - b) \\ &= e^{2\pi ib \cdot \xi}\int_{\mathbb{R}^d} e^{-2\pi iy \cdot \xi}f(y)dy \\ &= e^{2\pi ib \cdot \xi}\widehat{f}(\xi). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e11fc5c2af88c8cec3e46d365a534c3b_l3.png)
- (伸缩性)对任意
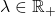 ,我们有
,我们有![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} [f(\lambda x)]^\wedge(\xi) &= \int_{\mathbb{R}^d} e^{-2\pi ix \cdot \xi}f(\lambda x)dx \\ &= \int_{\mathbb{R}^d} e^{-2\pi i(\lambda^{-1}y) \cdot \xi}f(y)d(\lambda^{-1}y) \\ &= \lambda^{-d}\int_{\mathbb{R}^d} e^{-2\pi iy \cdot (\lambda^{-1}\xi)}f(y)dy \\ &= \lambda^{-d}\widehat{f}(\lambda^{-1}\xi). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-370dde62c03cb3d0076c86404c828e13_l3.png)
- (旋转性)对任意
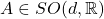 ,我们有
,我们有![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} [f(Ax)]^\wedge(\xi) &= \int_{\mathbb{R}^d} e^{-2\pi ix \cdot \xi}f(Ax)dx \\ &= \int_{\mathbb{R}^d} e^{-2\pi i(A^{-1}y) \cdot \xi}f(y)d(A^{-1}y) \\ &= \int_{\mathbb{R}^d} e^{-2\pi iy \cdot (A\xi)}f(y)dy \\ &= \widehat{f}(A\xi). \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d2ad4be55e76209002359f7fdb06083b_l3.png)
- 由定义可知,
- 如果
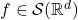 ,那么
,那么![Rendered by QuickLaTeX.com \[ [\partial_x^\alpha f(x)]^\wedge(\xi) = (2\pi i)^{|\alpha|}\xi^\alpha\widehat{f}(\xi), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-74007fa306fe50fef2150c4d349c04c0_l3.png)
![Rendered by QuickLaTeX.com \[ \partial_\xi^\alpha\widehat{f}(\xi) = (-2\pi i)^{|\alpha|}[x^\alpha f(x)]^\wedge(\xi). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-89b4d7376332ff30b078279276600bf1_l3.png)
- 第一个等式可以由分部积分得到
- 第二个等式可以由交换求导、积分次序得到。这里需要使用Lebesgue控制收敛定理
- 因此,
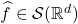 ,即Fourier变换是从
,即Fourier变换是从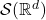 到
到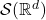 的变换
的变换
反演公式
- Gauss函数的Fourier变换为
![Rendered by QuickLaTeX.com \[ \widehat{e^{-\pi|x|^2}}(\xi) = e^{-\pi|\xi|^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d90b3b63292d8187aa386fd7e61cbb0f_l3.png)
- 由于
故我们只需证明1维情形![Rendered by QuickLaTeX.com \[ \int_{\mathbb{R}^d} e^{-2\pi ix \cdot \xi}e^{-\pi|x|^2}dx = \prod_{i = 1}^d\int_\mathbb{R} e^{-2\pi ix_i\xi_i}e^{-\pi x_i^2}dx_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a5da4db8bd76c805bd2221e6d442b3f5_l3.png)
- 转换为复变函数的积分
其中,![Rendered by QuickLaTeX.com \[ \int_\mathbb{R} e^{-2\pi ix_i\xi_i}e^{-\pi x_i^2}dx_i = e^{-\pi\xi_i^2}\int_\gamma e^{-\pi z^2}dz, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2c60ccfbaf943c8615bf091217056016_l3.png)
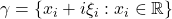
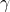 由
由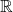 平移
平移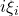 得到。由复数域上的分析中的Cauchy积分定理(
得到。由复数域上的分析中的Cauchy积分定理(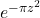 为全纯函数),我们可以将
为全纯函数),我们可以将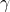 上的积分转换为
上的积分转换为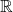 上的积分
上的积分![Rendered by QuickLaTeX.com \[ \int_\gamma e^{-\pi z^2}dz = \int_\mathbb{R} e^{-\pi t^2}dt = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d621f485f0bba828265b7c5fcc40741d_l3.png)
- 由于
- 如果
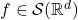 ,那么我们有反演公式
,那么我们有反演公式
如果记Fourier逆变换为![Rendered by QuickLaTeX.com \[ f(x) = \int_{\mathbb{R}^d} e^{2\pi ix \cdot \xi}\widehat{f}(\xi)d\xi,\; x \in \mathbb{R}^d. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6320e29cdddb7ec489ed49b71566906e_l3.png)
那么,![Rendered by QuickLaTeX.com \[ g^{\vee}(x) = \int_{\mathbb{R}^d} e^{2\pi ix \cdot \xi}g(\xi)d\xi, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ad61debd5014ccddc8aa763756e4601a_l3.png)
![Rendered by QuickLaTeX.com \[ (\widehat{f})^{\vee} = f,\; \overline{g^{\vee}} = \widehat{\overline{g}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5986a0a6cff190afe59e6de34410bbfa_l3.png)
- 反演公式的右端是一个累次积分,但是不能直接交换积分次序。因此,我们使用Lebesgue控制收敛定理,在其中插入一个Gauss函数
然后,使用Fubini定理交换积分次序,得到![Rendered by QuickLaTeX.com \[ \int_{\mathbb{R}^d} e^{2\pi ix \cdot \xi}\widehat{f}(\xi)d\xi = \lim_{\epsilon \to 0}\int_{\mathbb{R}^d} e^{2\pi ix \cdot \xi}e^{-\pi\epsilon^2|\xi|^2}\widehat{f}(\xi)d\xi. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-87c9848f90b41f5cd8ea129f21527c1c_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{\epsilon \to 0}\int_{\mathbb{R}^d}\int_{\mathbb{R}^d} e^{2\pi i(x - y)\cdot \xi}e^{-\pi\epsilon^2|\xi|^2}d\xi f(y)dy. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-83767785d3be82a43f77c3f1dd4dcace_l3.png)
- 注意,关于
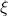 的积分实际上是Gauss函数的Fourier变换,
的积分实际上是Gauss函数的Fourier变换,
这里,![Rendered by QuickLaTeX.com \[ G_\epsilon(x - y) = \widehat{e^{-\pi\epsilon^2|\xi|^2}}(y - x) = \epsilon^{-d}e^{-\pi\epsilon^{-2}|x - y|^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-533bef8c97e2665a39c77c498909ec8c_l3.png)
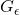 为Gauss核,我们只需证明
为Gauss核,我们只需证明
由于Gauss核![Rendered by QuickLaTeX.com \[ \lim_{\epsilon \to 0} G_\epsilon * f = f. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-60c127278f99c8adcbf7b95bc98c4f8d_l3.png)
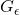 有着完全类似于Fejér核
有着完全类似于Fejér核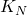 的性质,故我们可以仿照之前的证明,得到
的性质,故我们可以仿照之前的证明,得到![Rendered by QuickLaTeX.com \[ ||G_\epsilon * f - f||_\infty \to 0 \text{ as } \epsilon \to 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f849b21bd648f5e49f0bd1548c2f4ab3_l3.png)
- 反演公式的右端是一个累次积分,但是不能直接交换积分次序。因此,我们使用Lebesgue控制收敛定理,在其中插入一个Gauss函数
- 在不同的地方,Fourier变换和Fourier逆变换有不同的形式,主要是为了消去如下积分产生的常数
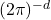 ,
,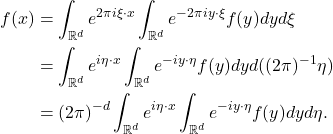
扩展Fourier变换的定义域
- 由上面的笔记可知,我们定义了Fourier变换
这里,![Rendered by QuickLaTeX.com \[ \mathcal{F}: \mathcal{S}(\mathbb{R}^d) \to \mathcal{S}(\mathbb{R}^d). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-871b72527548eb70e261025f84b8fb71_l3.png)
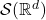 只包含各阶偏导数比所有幂函数下降都快的函数(比如Gauss函数),这一限制条件太强,我们希望扩展Fourier变换
只包含各阶偏导数比所有幂函数下降都快的函数(比如Gauss函数),这一限制条件太强,我们希望扩展Fourier变换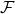 的定义域,使其能够作用在更加广泛的函数上
的定义域,使其能够作用在更加广泛的函数上 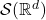 的限制条件越强,那么它的对偶空间
的限制条件越强,那么它的对偶空间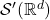 的限制条件就越弱。对偶空间
的限制条件就越弱。对偶空间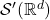 中的元素为
中的元素为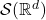 上的连续线性泛函。为此我们还需要定义
上的连续线性泛函。为此我们还需要定义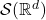 上的收敛性,
上的收敛性,![Rendered by QuickLaTeX.com \[ f_n \to f \Leftrightarrow ||x^\alpha\partial_x^\beta[f_n(x) - f(x)]||_\infty \to 0 \text{ for any } \alpha, \beta. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e2dbb392a146496f5ec6ae05d4eaed01_l3.png)
- 现在,我们用对偶空间
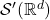 、原空间
、原空间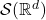 上的配对
上的配对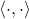 来定义
来定义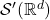 上的Fourier变换,
上的Fourier变换,
上面的定义确实扩展了Fourier变换![Rendered by QuickLaTeX.com \[ \langle{\widehat{f}, \varphi}\rangle = \langle{f, \widehat{\varphi}}\rangle,\; f \in \mathcal{S}'(\mathbb{R}^d),\; \varphi \in \mathcal{S}(\mathbb{R}^d). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5f37e1b327d292c56087014ee42c08e1_l3.png)
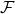 的定义域(比如增加了
的定义域(比如增加了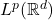 ),原因是它对
),原因是它对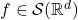 成立,
成立,
这里,我们需要将函数视为连续线性泛函。我们也可以得到![Rendered by QuickLaTeX.com \[ \langle{\widehat{f}, \varphi}\rangle = \int_{\mathbb{R}^d} \widehat{f}(x)\varphi(x)dx = \int_{\mathbb{R}^d} f(x)\widehat{\varphi}(x)dx = \langle{f, \widehat{\varphi}}\rangle. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e4fb21b5f66c0f566efc198b01fa094e_l3.png)
![Rendered by QuickLaTeX.com \[ \widehat{f * \varphi} = \widehat{f}\widehat{\varphi}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f0215aa4b714f69ed26f5839afcd04be_l3.png)
- (Dirac函数和1)
![Rendered by QuickLaTeX.com \[ \langle{\delta, \widehat{\varphi}}\rangle = \widehat{\varphi}(0) = \int_{\mathbb{R}^d} \varphi(x)dx = \langle{1, \varphi}\rangle,\; \widehat{\delta} = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6ae945985fcef4ae12ef019c9ce15a9f_l3.png)
![Rendered by QuickLaTeX.com \[ \langle{1, \widehat{\varphi}}\rangle = \int_{\mathbb{R}^d} \widehat{\varphi}(\xi)d\xi = \varphi(0) = \langle{\delta, \varphi}\rangle,\; \widehat{1} = \delta. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-24562b60bbe5d06853a812ab9ba86159_l3.png)
- (Plancherel定理)设
 、
、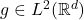 。那么,
。那么,
当![Rendered by QuickLaTeX.com \[ \langle{\widehat{f}, \widehat{g}}\rangle_{L^2} = \langle{f, g}\rangle_{L^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0f50265498bca5b176ec676e0a35e57e_l3.png)
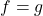 时,上式成为
时,上式成为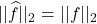
- 因为
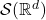 在
在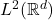 中稠密,所以我们只需考虑
中稠密,所以我们只需考虑 、
、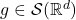 。此时,
。此时,![Rendered by QuickLaTeX.com \[ \langle{\widehat{f}, \widehat{g}}\rangle_{L^2} = \int \widehat{f} \cdot \overline{\widehat{g}} = \int f \cdot \widehat{\overline{\widehat{g}}} = \int f \cdot \overline{(\widehat{g})^{\vee}} = \int f \cdot \overline{g} = \langle{f, g}\rangle_{L^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b9f75ba971605c7b7bca011185ca602c_l3.png)
- 因为