多边形的三角剖分
- 三角剖分是利用对角线,将多边形完全剖分为三角形
- 多边形(不一定是凸的)存在一个三角剖分。如果顶点数为
 ,那么三角形数为
,那么三角形数为
- 首先,我们证明存在一条对角线,它完全落在多边形内部
- 取一个最左侧的顶点
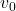 ,它有两个相邻的顶点
,它有两个相邻的顶点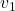 、
、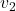 。对于三角形
。对于三角形![Rendered by QuickLaTeX.com [v_0, v_1, v_2]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-639d70949a7ee70d0a623e1cb2137b02_l3.png) ,如果它完全落在多边形内部,那么线段
,如果它完全落在多边形内部,那么线段![Rendered by QuickLaTeX.com [v_1, v_2]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-89c90000a631f47e968c060caf3a47df_l3.png) 完全落在多边形内部;如果它完全落在多边形外部,那么存在一个比
完全落在多边形内部;如果它完全落在多边形外部,那么存在一个比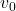 更左侧的顶点,与
更左侧的顶点,与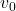 的取法矛盾
的取法矛盾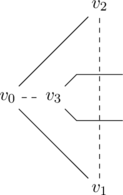
- 关键的情形在于,三角形
![Rendered by QuickLaTeX.com [v_0, v_1, v_2]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-639d70949a7ee70d0a623e1cb2137b02_l3.png) 既包含多边形内部的点,又包含多边形外部的点,从而包含多边形边界的点。注意,多边形的边界是不自交的,所以多边形的边界有若干条线段的顶点落在三角形
既包含多边形内部的点,又包含多边形外部的点,从而包含多边形边界的点。注意,多边形的边界是不自交的,所以多边形的边界有若干条线段的顶点落在三角形![Rendered by QuickLaTeX.com [v_0, v_1, v_2]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-639d70949a7ee70d0a623e1cb2137b02_l3.png) 内部。取一个距离线段
内部。取一个距离线段![Rendered by QuickLaTeX.com [v_1, v_2]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-89c90000a631f47e968c060caf3a47df_l3.png) 最远的顶点
最远的顶点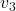 ,那么线段
,那么线段![Rendered by QuickLaTeX.com [v_0, v_3]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9a51a8aa4224c28f36c0d2cca237aae5_l3.png) 完全落在多边形内部
完全落在多边形内部
- 取一个最左侧的顶点
- 现在,我们回到命题的证明。当
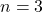 时,命题成立。如果
时,命题成立。如果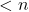 的情形成立,那么考虑
的情形成立,那么考虑 的情形
的情形
- 由上述可知,存在一条对角线,它完全落在多边形内部,所以它将多边形剖分为两个子多边形,顶点数分别为
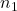 、
、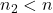 。由于对角线的2个顶点重复计算2次,故
。由于对角线的2个顶点重复计算2次,故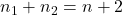
- 由归纳假设可知,子多边形可以完全剖分为三角形,三角形数分别为
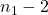 、
、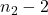 。因此,原多边形可以完全剖分为三角形,三角形数为
。因此,原多边形可以完全剖分为三角形,三角形数为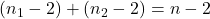 。由数学归纳法可知,命题成立
。由数学归纳法可知,命题成立
- 由上述可知,存在一条对角线,它完全落在多边形内部,所以它将多边形剖分为两个子多边形,顶点数分别为
- 首先,我们证明存在一条对角线,它完全落在多边形内部
Steiner树问题
- 网络
- 道路网络 –> 不同城市,用总长度最小的道路来互联
- 管道网络 –> 不同建筑,用总长度最小的给排水管道来互联
- 计算机网络 –> 不同主机,用总长度最小的光纤来互联
- 芯片网络 –> 不同器件,用总长度最小的导线来互联
- 在实际情形下,我们有更多的约束条件,并且目标不一定是总长度最小。不过,我们仍然可以考虑理想的最优化问题——在
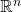 中的不同点(可以添加额外的点),用总长度最小的道路来互联,这称为Steiner树问题
中的不同点(可以添加额外的点),用总长度最小的道路来互联,这称为Steiner树问题
- 在
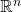 的Euclid度量下,两点之间线段最短。因此,我们考虑不同点用线段来互联,这构成一个图
的Euclid度量下,两点之间线段最短。因此,我们考虑不同点用线段来互联,这构成一个图 - 如果图上有环路,那么我们可以去掉环路上的一条道路。此时,不同点仍然是互联的,并且总长度减少。因此,我们考虑无环路的连通图,这构成一棵树
- 在
- 如果不添加额外的点,那么我们只需取所有点构成的完全图
 ,然后取
,然后取 中总长度最小的生成树
中总长度最小的生成树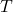 即可;在
即可;在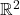 上,Delaunay三角剖分恰好包含
上,Delaunay三角剖分恰好包含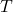 。因此,如果可以添加额外的点,那么这些点称为Steiner点,它们对应于Steiner三角剖分
。因此,如果可以添加额外的点,那么这些点称为Steiner点,它们对应于Steiner三角剖分
- 取Steiner三角剖分,这构成一个图
- 取图的一颗生成树,使得总长度最小
- 因此,关键在于应该在何处添加Steiner点,它们的作用类似于中继(Relay)
- 我们也可以将Steiner树视为通信网络的链路(Link)
- 对于近地卫星之间的通信,我们需要使用
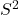 的球面度量
的球面度量 - 对于星际卫星之间的通信,如果用电磁波来通信,并且考虑广义相对论造成的时空弯曲,那么我们需要使用一般的Riemann度量
- 对于近地卫星之间的通信,我们需要使用
Steiner三角剖分
- 在
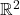 上,我们可以用一个正方形来包围给定的点。因此,我们只需考虑正方形内部的Steiner三角剖分,然后去掉给定的点的凸包外部的点、边即可
上,我们可以用一个正方形来包围给定的点。因此,我们只需考虑正方形内部的Steiner三角剖分,然后去掉给定的点的凸包外部的点、边即可
- 添加Steiner点,得到Steiner三角剖分,这相当于进行网格生成(Mesh Generation)。网格的作用很广泛,在计算机图形学中,它是曲面建模的基础;在数值计算中,它是有限元方法的基础
- 在计算机图形学的重心坐标中,光线追踪的BVH(Bounding Volume Hierarchy,包围体积层次结构)不断将
 中的AABB(Axis-Aligned Bounding Box,沿坐标轴对齐的包围盒)等分为8个子AABB,得到八叉树(Octree)。在这里,我们不断将
中的AABB(Axis-Aligned Bounding Box,沿坐标轴对齐的包围盒)等分为8个子AABB,得到八叉树(Octree)。在这里,我们不断将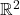 中的AABB等分为4个子AABB,得到四叉树(Quadtree)
中的AABB等分为4个子AABB,得到四叉树(Quadtree)