参考资料:Games101
计算机图形学的流程
- 计算机图形学的第一步是建模(Modeling)
- 对于
 中的曲面,我们可以使用参数表示、隐式方程
中的曲面,我们可以使用参数表示、隐式方程 - 对于复杂形体,我们通常使用三角形网格(Triangle Mesh)
- 对于
- 计算机图形学的第二步是可视化(Visualization)
- 渲染(Rendering),更接近于艺术(Art)
- 仿真(Simulation),更接近于计算物理(Computational Physics)
- 通常,图像需要呈现在显示器上,显示器是像素的矩阵。下面,我们考虑渲染的常用方法
- 光线追踪(Ray Tracing),像素 –> 模型
- 光栅化(Rasterization),模型 –> 像素
混合积和光线追踪
- 关于单纯形、重心坐标,可参见三角剖分和单纯复形
- 内积、外积、混合积
- 对于3维向量
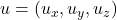 、
、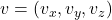 ,内积、外积分别为
,内积、外积分别为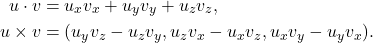
- 因为外积为反对称、线性的,它对应于行列式,所以外积可以用行列式来表示,
进一步,混合积![Rendered by QuickLaTeX.com \[ u \times v = \bigg(\det\begin{bmatrix} u_y & u_z \\ v_y & v_z \end{bmatrix}, \det\begin{bmatrix} u_z & u_x \\ v_z & v_x \end{bmatrix}, \det\begin{bmatrix} u_x & u_y \\ v_x & v_y \end{bmatrix}\bigg). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0f2547467f5fff400018b1fb67fd8866_l3.png)
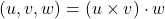 也可以用行列式来表示,
也可以用行列式来表示,
注意,混合积是轮换对称的,![Rendered by QuickLaTeX.com \[ (u, v, w) = \det\begin{bmatrix} u_x & u_y & u_z \\ v_x & v_y & v_z \\ w_x & w_y & w_z \end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e8b6c1b6892a94d9acc3e59ec2f6cff9_l3.png)
![Rendered by QuickLaTeX.com \[ (u, v, w) = (v, w, u) = (w, u, v). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f30820da74638f67cbc6b11f0f446e7b_l3.png)
- 对于3维向量
- Möller–Trumbore相交算法
- 在人眼处,向像素发射一条光线,求出光线和模型的三角形网格的交点
- 光线可以表示为射线,
其中,![Rendered by QuickLaTeX.com \[ O + tD, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dfde4c6538845d55c1517b64ce4148e5_l3.png)
 为时间
为时间 - 三角形可以表示为2-单纯形,
其中,![Rendered by QuickLaTeX.com \[ (1 - b_1 - b_2)P_0 + b_1P_1 + b_2P_2, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-75c4d99dfa6a6aca8f4e47117ad27ea6_l3.png)
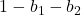 、
、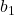 、
、![Rendered by QuickLaTeX.com b_2 \in [0, 1]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-976898c1458ffc97dc252e9052820935_l3.png) 为重心坐标
为重心坐标 - 在交点处,
即![Rendered by QuickLaTeX.com \[ O + tD = (1 - b_1 - b_2)P_0 + b_1P_1 + b_2P_2, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-41aa31c02db8e1d460c006c6231e72b1_l3.png)
其中,![Rendered by QuickLaTeX.com \[ tD = -S + b_1E_1+ b_2E_2, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8841fbd8d7725a66656e9be8e2e2488a_l3.png)
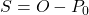 、
、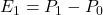 、
、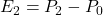
- 光线可以表示为射线,
- 上面的方程为
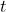 、
、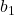 、
、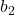 的线性方程。根据Cramer法则,我们可以用行列式来求解线性方程。因为混合积即行列式,所以我们也可以使用混合积
的线性方程。根据Cramer法则,我们可以用行列式来求解线性方程。因为混合积即行列式,所以我们也可以使用混合积
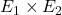 垂直于
垂直于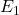 、
、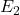 。将方程与其作内积,可得
。将方程与其作内积,可得![Rendered by QuickLaTeX.com \[ t = \frac{-S \cdot (E_1 \times E_2)}{D \cdot (E_1 \times E_2)}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0225275661a6f6ba75a55ab79fe05242_l3.png)
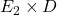 垂直于
垂直于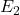 、
、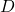 。将方程与其作内积,可得
。将方程与其作内积,可得![Rendered by QuickLaTeX.com \[ b_1 = \frac{S \cdot (E_2 \times D)}{E_1 \cdot (E_2 \times D)}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c65e232f6b88d571563f0e3b24bab59c_l3.png)
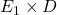 垂直于
垂直于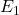 、
、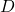 。将方程与其作内积,可得
。将方程与其作内积,可得![Rendered by QuickLaTeX.com \[ b_2 = \frac{S \cdot (E_1 \times D)}{E_2 \cdot (E_1 \times D)}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ad1340f14cfbc6b0628a8ef913eabe1f_l3.png)
- 在人眼处,向像素发射一条光线,求出光线和模型的三角形网格的交点
- Möller–Trumbore相交算法的计算复杂度
- 对于3维向量,内积为5flops、外积为9flops、加减为3flops
- 利用混合积的轮换对称性,我们可以减少外积的重复计算。令
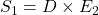 、
、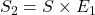 ,那么
,那么![Rendered by QuickLaTeX.com \[ t = \frac{E_2 \cdot S_2}{E_1 \cdot S_1},\; b_1 = \frac{S \cdot S_1}{E_1 \cdot S_1},\; b_2 = \frac{D \cdot S_2}{E_1 \cdot S_1}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8da8c032ff8963cc480c28b7c6b6b1a6_l3.png)
- 我们需要计算2次外积 = 18flops、4次内积 = 20flops、3次除法 = 3flops,再加上开始的3次减法 = 9flops。因此,Möller–Trumbore相交算法的计算复杂度为50flops
- 在光线追踪中,我们既需要遍历每个像素,也需要遍历每个三角形。因此,光线追踪的计算复杂度至少为
对于分辨率1920 * 1080、帧率60、三角形数量100万,光线追踪的计算复杂度至少为![Rendered by QuickLaTeX.com \[ Pixels \times Triangles \times 50flops. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-057b5d93cbe7f8e51d524d9f31eba42c_l3.png)
因此,在实时渲染中,我们需要光线追踪的加速计算![Rendered by QuickLaTeX.com \[ 1920 \times 1080 \times 60 \times 10^6 \times 50flops \approx 6 \times 10^{15}flops = 6Pflops. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c5ee6babd99a076ffc8cf9f088b7b946_l3.png)
- 对于每个像素,我们可以使用GPU的并行化
- 对于每个三角形,我们可以使用GPU的BVH(Bounding Volume Hierarchy,包围体积层次结构)
- 对于Möller–Trumbore相交算法,我们可以使用GPU的光线追踪核心(Ray Tracing Core,RT Core)
传统的图形渲染管线
- 关于图形软件栈,可参见Mesa用户态驱动
- 光栅化是传统的图形渲染管线的中心环节
- GPU的顶点着色器(Vertex Shader,VS)
- 顶点 –> 顶点
- 进行计算机图形学的MVP变换等
- GPU的几何着色器(Geometry Shader,GS)、细分着色器(Tessellation Shader,TS)
- 顶点 –> 图元
- 进行图元组装、曲面细分等
- GPU的光栅化
- 图元 –> 像素
- 进行像素测试、属性插值等
- GPU的片段着色器(Fragment Shader,FS)
- 像素 –> 图像
- 进行纹理贴图、光照计算等。在附加-Game Engine Black Book Doom中,纹理、光照提供了主要的视觉效果
- 最终的图像存放在帧缓冲区(Framebuffer),它对应于显示的一帧
- 颜色缓冲区(Color Buffer),由纹理、光照产生
- 深度缓冲区(Depth Buffer),由
 坐标产生
坐标产生 - 为了将一帧呈现在显示器上,我们先将其存放在后缓冲区(Back Buffer),等到需要显示的时候,再将其交换到前缓冲区(Front Buffer)
- 上面的图形渲染管线是固定的。如果需要使用更加通用的图形渲染管线,那么可以使用GPU的计算着色器(Compute Shader,CS),它类似于通用计算中的CUDA核心(CUDA Core)
- GPU的顶点着色器(Vertex Shader,VS)
- 在计算机图形学的MVP变换的最后一步,投影变换可以将视觉体积变为AABB(Axis-Aligned Bounding Box,沿坐标轴对齐的包围盒)
- 因为照片的尺寸、显示器的分辨率各不相同,所以我们使用一个标准的接口,即NDC(Normalized Device Coordinates,归一化设备坐标)
- (AABB –> NDC)如果近底面的左、右、下、上的坐标分别为
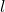 、
、 、
、 、
、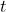 ,那么AABB为
,那么AABB为![Rendered by QuickLaTeX.com [l, r] \times [b, t] \times [f, n]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2a3c1a867c234606b8eb0f4ac91fd933_l3.png) 。我们使用一个平移、一个伸缩,将AABB变为单位立方体
。我们使用一个平移、一个伸缩,将AABB变为单位立方体![Rendered by QuickLaTeX.com [-1, 1]^3](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-351abc919d0d13dc3f9eae26e17cc762_l3.png) 。通常,我们将其和投影变换合并在一起,作为最终的投影变换
。通常,我们将其和投影变换合并在一起,作为最终的投影变换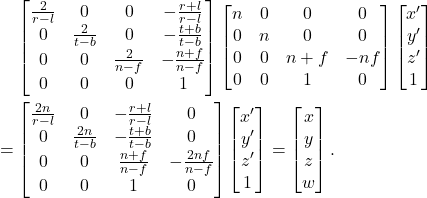
- (NDC –> 屏幕)如果显示器的分辨率为
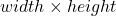 ,深度范围为
,深度范围为![Rendered by QuickLaTeX.com [z_{far}, z_{near}]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9902ff18abbf2f8de6746d81fb10be4b_l3.png) ,那么我们可以使用一个平移、一个伸缩,将单位立方体
,那么我们可以使用一个平移、一个伸缩,将单位立方体![Rendered by QuickLaTeX.com [-1, 1]^3](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-351abc919d0d13dc3f9eae26e17cc762_l3.png) 变为
变为![Rendered by QuickLaTeX.com [0, width] \times [0, height] \times [z_{far}, z_{near}]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-028859f2702000de11fefc8e9ea82a32_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{bmatrix}\frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & \frac{z_{near} - z_{far}}{2} & \frac{z_{near} + z_{far}}{2} \\ 0 & 0 & 0 & 1\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-042af63ec99bce48f8bf6dd4dabfb4a6_l3.png)
- 第一步由应用程序的VS控制,第二步由GPU控制。在二者之间,GPU还需要进行裁剪(只保留
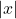 、
、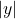 、
、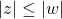 的部分)、齐次除法(将
的部分)、齐次除法(将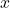 、
、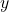 、
、 除以
除以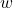 )
)
- 在GPU中,除法器比乘法器更慢,所以齐次除法通常先取
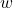 的倒数
的倒数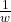 (1次除法),然后将
(1次除法),然后将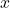 、
、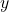 、
、 乘以
乘以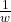 (3次乘法)。在上面的Möller–Trumbore相交算法中,我们也可以将3次除法转换为1次除法、3次乘法
(3次乘法)。在上面的Möller–Trumbore相交算法中,我们也可以将3次除法转换为1次除法、3次乘法
- 在GPU中,除法器比乘法器更慢,所以齐次除法通常先取
- 在不同的图形API中,
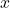 、
、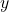 、
、 、
、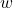 的约定是不同的。在这里,我们使用如下约定
的约定是不同的。在这里,我们使用如下约定
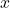 、
、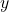 坐标的原点位于屏幕的左下角
坐标的原点位于屏幕的左下角 坐标为负数,它的绝对值越大,距离越远;从而,它本身越小,距离越远
坐标为负数,它的绝对值越大,距离越远;从而,它本身越小,距离越远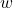 坐标为
坐标为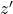 –> 投影变换 –>
–> 投影变换 –> 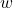 –> 取倒数 –>
–> 取倒数 –> 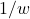 。因此,
。因此,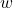 坐标为视觉空间的
坐标为视觉空间的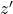 坐标的倒数
坐标的倒数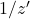
混合积和Lebesgue测度
- 关于单纯形、重心坐标,可参见三角剖分和单纯复形
- 现在,我们已经位于屏幕之上,接下来需要将图元(点、线段、三角形、多边形)变为像素
- 点、线段 –> 增加宽度 –> 多边形 –> 三角剖分 –> 三角形。因此,我们只需考虑三角形的光栅化
- 第一步是像素测试,使用2-单纯形的重心坐标,判断像素是否位于三角形中
- 第二步是属性插值,使用2-单纯形的重心坐标,将三角形顶点的属性值插值为像素的属性值
- 行列式的几何意义
- 由Lebesgue测度可知,在仿射变换下,Lebesgue测度的变化倍数为行列式的绝对值,
![Rendered by QuickLaTeX.com \[ \lambda(A\Omega + b) = |\det(A)| \cdot \lambda(\Omega). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-486f788c59fc1ec41bf6be3aaf800172_l3.png)
- 如果
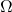 为标准单位正交基生成的平行体(Lebesgue测度为1),那么
为标准单位正交基生成的平行体(Lebesgue测度为1),那么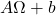 为
为 的列向量生成平行体(Lebesgue测度为
的列向量生成平行体(Lebesgue测度为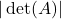 )。因此,行列式的几何意义为平行体的有向Lebesgue测度
)。因此,行列式的几何意义为平行体的有向Lebesgue测度
- 在2维时,行列式 –> 外积,平行体的有向Lebesgue测度 –> 平行四边形的有向面积。因此,平行四边形的有向面积可以用外积来表示
![Rendered by QuickLaTeX.com \[ (u_x, u_y, 0) \times (v_x, v_y, 0). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7556bb64f32e86de30cc2ee1488e1fd9_l3.png)
- 在3维时,行列式 –> 混合积,平行体的有向Lebesgue测度 –> 平行六面体的有向体积。因此,平行六面体的有向体积可以用混合积来表示
![Rendered by QuickLaTeX.com \[ [(u_x, u_y, u_z) \times (v_x, v_y, v_z)] \cdot (w_x, w_y, w_z). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-17f7b854ffd484fa1cd84684d60eacc7_l3.png)
- 在2维时,行列式 –> 外积,平行体的有向Lebesgue测度 –> 平行四边形的有向面积。因此,平行四边形的有向面积可以用外积来表示
- 由一般的测度和积分中的Fubini定理,我们可以计算一般的单纯形的有向Lebesgue测度
- 由Lebesgue测度可知,在仿射变换下,Lebesgue测度的变化倍数为行列式的绝对值,
- //
- 重心坐标的几何意义
- 一般的重心坐标为一般的单纯形的有向Lebesgue测度比
透视校正插值
- 由Euclid几何、晶体群可知,有向Lebesgue测度比是仿射不变量,但不是射影不变量
- 模型变换(M)、视觉变换(V) –> 仿射变换
- 投影变换(P) –> 射影变换
- 因此,重心坐标在投影变换后会改变,我们需要进行透视校正插值。在附加-Game Engine Black Book Doom中,透视校正插值可以获得正确的纹理映射,防止纹理扭曲