局部平凡丛
- 由计算机图形学的几何变换可知,计算机图形学可以将
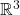 中的模型渲染为
中的模型渲染为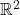 中的图像,其原理类似于相机拍摄模型的照片。因为投影变换可以让我们从3维降低到2维,所以它是下面第一种成像方法
中的图像,其原理类似于相机拍摄模型的照片。因为投影变换可以让我们从3维降低到2维,所以它是下面第一种成像方法
- 摄影成像(Photography)观察投影
![Rendered by QuickLaTeX.com \[ p: \mathbb{R}^3 \to \mathbb{R}^2,\; (x, y, z) \mapsto (x, y). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-817b10b126e10404fbf52ad91b54c2aa_l3.png)
- 断层成像(Tomography)观察截面
![Rendered by QuickLaTeX.com \[ s: \mathbb{R}^2 \to \mathbb{R}^3,\; (x, y) \mapsto (x, y, f(x, y)). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7fe8e8031ed5acc2364b4a47e944852a_l3.png)
- 全息成像(Holography)观察整个空间
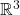
- 摄影成像(Photography)观察投影
- 如果全空间
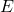 为
为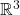 (类似于成像的整个空间),底空间
(类似于成像的整个空间),底空间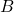 为
为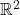 (类似于成像的底片),那么我们可以得到整体平凡丛(即乘积丛)
(类似于成像的底片),那么我们可以得到整体平凡丛(即乘积丛)
其中,纤维![Rendered by QuickLaTeX.com \[ p: E \to B,\; E = B \times F, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-73b7c2d475ee018294f026d630a5c4b9_l3.png)
 为
为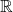
- 一般的纤维丛为局部平凡丛(即在局部上为乘积丛)
它类似于流形上的整体结构中的流形![Rendered by QuickLaTeX.com \[ p: E \to B, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-51d9d748290979b8cc86dfaed9eba806_l3.png)
- (局部平凡化邻域)我们有开覆盖
![Rendered by QuickLaTeX.com \[ B = \cup_i U_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b255516dbd358b091d8bee5701ee22a4_l3.png)
- (局部平凡化映射)我们有同胚,从乘积丛到
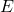 的开集
的开集
其中,![Rendered by QuickLaTeX.com \[ \varphi_i: U_i \times F \to p^{-1}(U_i) \subset E, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a58f47cacf269c1c7987781ce5c7cd11_l3.png)
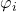 是保持纤维的,
是保持纤维的,
也就是说,![Rendered by QuickLaTeX.com \[ p \circ \varphi_i(x, f) = x,\; (x, f) \in U_i \times F. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-af76b92a9fead88e788232575244044e_l3.png)
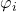 将
将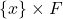 映射到
映射到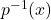 ,二者都同胚于
,二者都同胚于 ,所以都叫做
,所以都叫做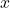 上的纤维
上的纤维 - 纤维丛的截面满足
纤维丛的截面(在局部)是某个函数![Rendered by QuickLaTeX.com \[ s: B \to E,\; p \circ s = id_B. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2635668ff0ea5ba84d24176569dc4cf2_l3.png)
 的图像,这和断层成像的截面一致,
的图像,这和断层成像的截面一致,![Rendered by QuickLaTeX.com \[ \varphi_i^{-1} \circ s: U_i \to U_i \times F,\; x \mapsto (x, f(x)). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-71e1aa61eba14c90043c9169bf658998_l3.png)
- (局部平凡化邻域)我们有开覆盖
- 如果
 具有离散拓扑,那么对任意局部平凡化的坐标卡
具有离散拓扑,那么对任意局部平凡化的坐标卡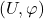 ,令
,令
我们有如下开集的不交并![Rendered by QuickLaTeX.com \[ U_\alpha = \varphi(U \times \{ \alpha \}),\; \alpha \in F. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-52e5870561e262096f9d2c1e3027af30_l3.png)
其中,![Rendered by QuickLaTeX.com \[ p^{-1}(U) = \coprod_\alpha U_\alpha, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4e829f618b8bc7a1945235cfebb06c85_l3.png)
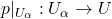 为同胚。因为
为同胚。因为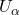 (数量为
(数量为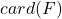 )同时投影到
)同时投影到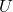 ,就像同时覆盖在
,就像同时覆盖在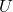 上一样,所以
上一样,所以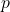 称为覆盖映射。进一步,当
称为覆盖映射。进一步,当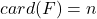 时,
时,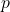 称为
称为 重覆盖映射
重覆盖映射
带结构群的纤维丛
- 现在,我们考虑转移映射
因为![Rendered by QuickLaTeX.com \[ \varphi_j^{-1} \circ \varphi_i: (U_i \cap U_j) \times F \to (U_i \cap U_j) \times F. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-575654753fb74ee32713c0dee9c0ab10_l3.png)
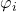 、
、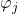 为保纤维的,所以转移映射保持基点
为保纤维的,所以转移映射保持基点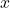 ,并且在
,并且在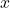 上是纤维
上是纤维 的同胚,
的同胚,![Rendered by QuickLaTeX.com \[ \varphi_j^{-1} \circ \varphi_i: (x, f) \mapsto (x, f'). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ceb7ba8a8b98a3f560c5b586c11435bb_l3.png)
- 如果我们将转移映射记为
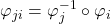 ,那么它对应于一个转移函数
,那么它对应于一个转移函数
进一步,带结构群![Rendered by QuickLaTeX.com \[ \overline{\varphi}_{ji}: U_i \cap U_j \to Homeo(F), \text{ where } f' = \overline{\varphi}_{ji}(x) \cdot f. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f60667207d1789051032aa80f075d5dd_l3.png)
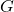 的纤维丛将转移函数约化为
的纤维丛将转移函数约化为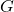 ,
,
因此,我们需要![Rendered by QuickLaTeX.com \[ \overline{\varphi}_{ji}: U_i \cap U_j \to G, \text{ where } f' = \overline{\varphi}_{ji}(x) \cdot f. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4e4d303df9f42887cf8b2bbe02b81948_l3.png)
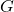 在
在 上的左作用
上的左作用 - 在计算机图形学中,
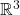 中的曲面
中的曲面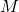 可以用参数表示来描述。我们考虑如下曲面,它们的底空间
可以用参数表示来描述。我们考虑如下曲面,它们的底空间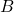 为1维圆环
为1维圆环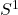 ,纤维
,纤维 为区间
为区间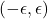 ,但是结构群不同,故全空间不同
,但是结构群不同,故全空间不同
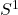 的角度范围
的角度范围
- 如果
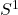 的角度范围为
的角度范围为
那么![Rendered by QuickLaTeX.com \[ [0, 2\pi] \to S^1,\; \theta \mapsto (\cos\theta, \sin\theta), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d44f757cb598bdb479459db36fa195ce_l3.png)
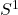 同胚于商空间
同胚于商空间![Rendered by QuickLaTeX.com \[ [0, 2\pi] / \sim, \text{ where } 0 \sim 2\pi. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b8780ce7961798b71f28707b1ace4591_l3.png)
- 如果
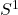 的角度范围为
的角度范围为
那么![Rendered by QuickLaTeX.com \[ \mathbb{R} \to S^1,\; \theta \mapsto (\cos\theta, \sin\theta), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-146c1f15f037aa68f7c4f1c882f21e41_l3.png)
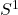 同胚于商群
同胚于商群![Rendered by QuickLaTeX.com \[ \mathbb{R} / 2\pi\mathbb{Z}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-496b63b3ca1a97d1d0171bba4ad5be80_l3.png)
- 如果
- 平环(Annulus)
- 参数为
![Rendered by QuickLaTeX.com \theta \in [0, 2\pi]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-14a655c3999d22818e27ba72ec277dee_l3.png) 、
、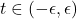 ,全空间
,全空间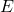 为
为
它可以看成区间![Rendered by QuickLaTeX.com \[ (\cos\theta, \sin\theta, t) \in \mathbb{R}^3. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-880e2131ac460b0fb2cb65c9051689dc_l3.png)
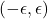 绕
绕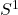 公转,在
公转,在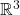 中扫过的曲面
中扫过的曲面
- 参数为
- Möbius环(Möbius Band)
- 参数为
![Rendered by QuickLaTeX.com \theta \in [0, 2\pi]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-14a655c3999d22818e27ba72ec277dee_l3.png) 、
、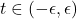 ,全空间
,全空间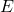 为
为
它可以看成区间![Rendered by QuickLaTeX.com \[ (\cos\theta(1 + \sin(\theta / 2)t), \sin\theta(1 + \sin(\theta / 2)t), \cos(\theta / 2)t) \in \mathbb{R}^3. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-84b10ff59bca9a3e6844246b88d8e0d8_l3.png)
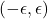 绕
绕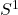 公转,并且以一半的角速度自转,在
公转,并且以一半的角速度自转,在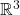 中扫过的曲面
中扫过的曲面 - Möbius环的一个显著特征是,当
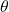 变为
变为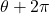 时,
时,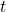 变为
变为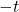 。比如,
。比如,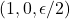 转一圈后变为
转一圈后变为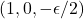 ,转两圈后变为
,转两圈后变为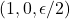
- Möbius环的另一个显著特征是,
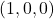 转一圈后变为
转一圈后变为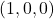 ,但是沿着
,但是沿着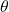 方向的切向量不变,沿着
方向的切向量不变,沿着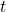 方向的切向量反向,故二者作外积得到的法向量反向。由此可知,在
方向的切向量反向,故二者作外积得到的法向量反向。由此可知,在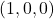 处我们无法定义法向量的方向,Möbius环是不可定向曲面
处我们无法定义法向量的方向,Möbius环是不可定向曲面
- 参数为
- 为了考察结构群,我们需要确定转移映射。取
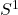 的局部平凡化邻域
的局部平凡化邻域
那么,![Rendered by QuickLaTeX.com \[ U_1= (\pi / 2 - \delta, 3\pi / 2 + \delta),\; U_2 = (3\pi / 2 - \delta, 5\pi / 2 + \delta). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3359c3782bc47e61c352eac40ee36d71_l3.png)
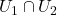 包含两部分
包含两部分
- 在
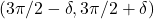 上,平环、Möbius环的
上,平环、Möbius环的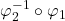 都为
都为![Rendered by QuickLaTeX.com \[ (\theta, t) \mapsto (\theta, t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-125fbfaf249fd34fd0905805a0184c41_l3.png)
- 在
 上,平环的
上,平环的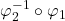 为
为
Möbius环的![Rendered by QuickLaTeX.com \[ (\theta, t) \mapsto (\theta, t), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-35d3ebc100824c8f7ee01aa2c609ab6a_l3.png)
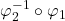 为
为![Rendered by QuickLaTeX.com \[ (\theta, t) \mapsto (\theta + 2\pi, -t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-acf5b12257a1a5eb14ac1d2f06ee6cef_l3.png)
- 在
- 最终,平环的结构群为平凡群
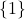 ,Möbius环的结构群为非平凡群
,Möbius环的结构群为非平凡群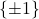
微分纤维丛、向量丛
- 通常,带结构群
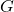 的纤维丛由微分流形产生,这样的纤维丛称为微分纤维丛
的纤维丛由微分流形产生,这样的纤维丛称为微分纤维丛 - 微分纤维丛包括切丛、余切丛、
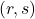 -型张量丛等。它们的纤维都是向量空间,它们的结构群都是一般线性群,所以它们也叫做向量丛。类似于数值线性代数,我们将向量空间的
-型张量丛等。它们的纤维都是向量空间,它们的结构群都是一般线性群,所以它们也叫做向量丛。类似于数值线性代数,我们将向量空间的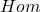 、
、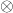 移植到向量丛上
移植到向量丛上
- 切丛
- 底空间
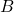 为微分流形
为微分流形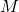 ,纤维
,纤维 为切空间
为切空间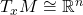 ,全空间
,全空间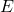 为切丛
为切丛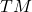
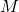 的坐标卡诱导
的坐标卡诱导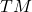 的坐标卡,
的坐标卡,![Rendered by QuickLaTeX.com \[ (x, v) \mapsto \sum_{i = 1}^n v^i\frac{\partial}{\partial x^i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8d9f08a7fef4ee9bbdaf10d68e6013cd_l3.png)
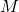 的转移映射诱导
的转移映射诱导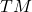 的转移映射,
的转移映射,
其中,我们有切向量的坐标变换公式![Rendered by QuickLaTeX.com \[ (x, v) \mapsto (x, w), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bb07785d0c0100ca3b55608b1d54a9ae_l3.png)
因为这是一个可逆的线性变换,所以切丛的结构群为![Rendered by QuickLaTeX.com \[ w^j = \sum_{i = 1}^n v^i\frac{\partial y^j}{\partial x^i}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-88287db44a0752d023349bfff18c9e84_l3.png)
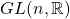
- 底空间
- 余切丛
- 底空间
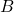 为微分流形
为微分流形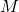 ,纤维
,纤维 为余切空间
为余切空间
全空间![Rendered by QuickLaTeX.com \[ T_x^*M = Hom(T_xM, \mathbb{R}) \cong \mathbb{R}^n, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2d1cd4d950422bbf713705b11fe4cb05_l3.png)
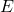 为余切丛
为余切丛![Rendered by QuickLaTeX.com \[ T^*M = Hom(TM, \mathbb{R}). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-43defd6ba2bd1caec09c88bb7224e29c_l3.png)
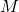 的坐标卡诱导
的坐标卡诱导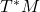 的坐标卡,
的坐标卡,![Rendered by QuickLaTeX.com \[ (x, v) \mapsto \sum_{i = 1}^n v_idx^i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e602f8969fb6d1592c108bbfb9e1913e_l3.png)
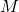 的转移映射诱导
的转移映射诱导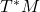 的转移映射,
的转移映射,
其中,我们有余切向量的坐标变换公式![Rendered by QuickLaTeX.com \[ (x, v) \mapsto (x, w), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bb07785d0c0100ca3b55608b1d54a9ae_l3.png)
因为这是一个可逆的线性变换,所以余切丛的结构群为![Rendered by QuickLaTeX.com \[ w_j = \sum_{i = 1}^n v_i\frac{\partial x^i}{\partial y^j}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-54d3c43019d47b394066af02a8160ffc_l3.png)
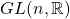
- 底空间
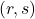 -型张量丛
-型张量丛
- 底空间
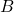 为微分流形
为微分流形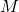 ,纤维
,纤维 为
为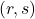 -型张量空间
-型张量空间
全空间![Rendered by QuickLaTeX.com \[ (T_r^s)_xM = T_xM \otimes \cdots \otimes T_xM \otimes T_x^*M \otimes \cdots \otimes T_x^*M \cong \mathbb{R}^{n^{r + s}}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-159be1fb09d74dd6225b9e91f9a8be18_l3.png)
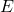 为
为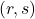 -型张量丛
-型张量丛![Rendered by QuickLaTeX.com \[ T_r^sM = TM \otimes \cdots \otimes TM \otimes T^*M \otimes \cdots \otimes T^*M. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1b8b8f994b1d773048094b7868d3c312_l3.png)
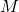 的坐标卡诱导
的坐标卡诱导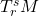 的坐标卡,
的坐标卡,![Rendered by QuickLaTeX.com \[ (x, v) \mapsto \sum_{i_1, \ldots, j_s = 1}^n v_{j_1 \ldots j_s}^{i_1 \ldots i_r}\frac{\partial}{\partial x^{i_1}} \otimes \cdots \otimes dx^{j_s}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-706e883ea86c9a3a68275aa22e5fb699_l3.png)
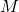 的转移映射诱导
的转移映射诱导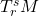 的转移映射,
的转移映射,
其中,我们有![Rendered by QuickLaTeX.com \[ (x, v) \mapsto (x, w), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bb07785d0c0100ca3b55608b1d54a9ae_l3.png)
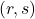 -型张量的坐标变换公式
-型张量的坐标变换公式
因为这是一个可逆的线性变换,所以![Rendered by QuickLaTeX.com \[ w_{l_1 \ldots l_s}^{k_1 \ldots k_r} = \sum_{i_1, \ldots, j_s = 1}^n v_{j_1 \ldots j_s}^{i_1 \ldots i_r}\frac{\partial y^{k_1}}{\partial x^{i_1}} \cdots \frac{\partial x^{j_s}}{\partial y^{l_s}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-efdfce2a6a8ec31f92bc592f9b855ce9_l3.png)
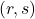 -型张量丛的结构群为
-型张量丛的结构群为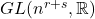
- 底空间
- 切丛