Fourier级数的定义
- 周期函数
- 对于1维环面
相差一个整数的点是等价的。因此,![Rendered by QuickLaTeX.com \[ \mathbb{T} = \mathbb{R}/\mathbb{Z} \cong S^1, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c1047a2d5b0f6a943cafa8cf21a6ce41_l3.png)
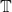 上的函数为周期为1的1维函数,它可以展开为1维Fourier级数
上的函数为周期为1的1维函数,它可以展开为1维Fourier级数 - 对于
 维环面
维环面
相差一个整数向量的点是等价的。因此,![Rendered by QuickLaTeX.com \[ \mathbb{T}^n = \mathbb{R}^n/\mathbb{Z}^n \cong (S^1)^n, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-11ccda59adc37b71139cde3bf2617f19_l3.png)
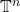 上的函数为周期为1的
上的函数为周期为1的 维函数,它可以展开为
维函数,它可以展开为 维Fourier级数
维Fourier级数 - 因为周期性可以用加法来刻画(1维环面
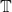 、
、 维环面
维环面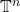 为Abel群),所以调和分析可以建立在(局部紧的)Abel群上。在这里,我们只考虑1维环面
为Abel群),所以调和分析可以建立在(局部紧的)Abel群上。在这里,我们只考虑1维环面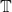 的情形,上面的指数周期函数为
的情形,上面的指数周期函数为![Rendered by QuickLaTeX.com \[ e(x) = e^{2\pi ix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9f4add3078a9639829545ce01a66d01e_l3.png)
- 对于1维环面
- 如果
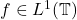 ,那么
,那么 的Fourier级数为
的Fourier级数为
其中,![Rendered by QuickLaTeX.com \[ \sum_{n = -\infty}^{+\infty} \widehat{f}(n)e(nx), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-11af2cae80c3f62546b7751afd93638e_l3.png)
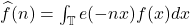 。Fourier级数的部分和为
。Fourier级数的部分和为
我们希望得到Fourier级数的收敛性![Rendered by QuickLaTeX.com \[ S_Nf(x) = \sum_{n = -N}^N \widehat{f}(n)e(nx). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7cc46193f0ade508153cbd42bd1dae03_l3.png)
![Rendered by QuickLaTeX.com \[ S_Nf \to f \text{ as } N \to \infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7c885a1b52e8fe2efec67c70d76ea422_l3.png)
Dirichlet核
- Dirichlet核为
它与![Rendered by QuickLaTeX.com \[ D_N(x) = \sum_{n = -N}^N e(nx). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fd8fdee3a936d786914b3961cf2d7b75_l3.png)
 的卷积为部分和,
的卷积为部分和,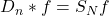
- Dirichlet核的不同形式
![Rendered by QuickLaTeX.com \[ D_N(x) = 1 + \sum_{n = 1}^N 2\cos(2n\pi x) = \frac{\sin[(2N + 1)\pi x]}{\sin(\pi x)}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b6e1e9c31ab35394c9d0dd6dd839fec6_l3.png)
- 由此可知,
因为![Rendered by QuickLaTeX.com \[ \int_\mathbb{T} D_N(x)dx = \int_\mathbb{T} 1dx + 2\sum_{n = 1}^n\int_\mathbb{T} \cos(2n\pi x)dx = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ab40e98b33c772f4a87ea703d7d4c283_l3.png)
![Rendered by QuickLaTeX.com \[ \int_{-\frac 12}^{\frac 12} |D_N(x)|dx \leq C\bigg(\int_0^{\frac 1N} Ndx + \int_{\frac 1N}^{\frac 12} x^{-1}dx\bigg) \leq C\ln N, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bdd30042828dd5aa8bf4430430040b10_l3.png)
所以![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} \int_{-\frac 12}^{\frac 12} |D_N(x)|dx &\geq C\sum_{i = 0}^{N - 1}\int_{\frac{i}{2N + 1}}^{\frac{i + 1}{2N + 1}} \frac{|\sin[(2N + 1)\pi x]|}{\pi x}dx \\ &\geq C\sum_{i = 0}^{N - 1}\int_{\frac{i}{2N + 1}}^{\frac{i + 1}{2N + 1}} \frac{|\sin[(2N + 1)\pi x]|}{\frac{i + 1}{2N + 1}}dx \\ &= C\sum_{i = 0}^{N - 1} \frac{1}{i + 1} \geq C\ln N, \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5e2f5ec0e49aadbe93eccbe308218504_l3.png)
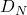 的
的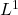 范数等价于
范数等价于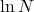
Fejér核
- Fejér核为
它与![Rendered by QuickLaTeX.com \[ K_N(x) = \frac 1N\sum_{n = 0}^{N - 1} D_n(x). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d812e75c21b8e963b2e5294b10b9e998_l3.png)
 的卷积为Cesàro和,
的卷积为Cesàro和,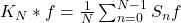
- Fejér核的不同形式
![Rendered by QuickLaTeX.com \[ K_N(x) = \frac 1N\frac{\sum_{n = 0}^{N - 1} \sin[(2n + 1)\pi x]}{\sin(\pi x)} = \frac 1N\bigg[\frac{\sin(N\pi x)}{sin(\pi x)}\bigg]^2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-af2382853e482e40e5a8977153488e06_l3.png)
- 由Dirichlet核可知,
因为![Rendered by QuickLaTeX.com \[ \int_\mathbb{T} K_N(x)dx = \frac 1N\sum_{n = 0}^{N - 1}\int_\mathbb{T} D_n(x)dx = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-54fd6e727c038b10ea5e6f3e5b328eda_l3.png)
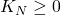 ,所以
,所以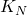 的
的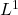 范数为1
范数为1
Fourier级数的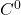 收敛
收敛
- 如果
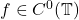 ,那么
,那么![Rendered by QuickLaTeX.com \[ ||K_N * f - f||_\infty \to 0 \text{ as } N \to \infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-6dd902212b02c84b54aa8a2c8b85e4e6_l3.png)
- 注意到
对于![Rendered by QuickLaTeX.com \[ |(K_N * f)(x) - f(x)| \leq \bigg(\int_{|y| < \delta} + \int_{|y| \geq \delta}\bigg) |f(x - y) - f(x)||K_N(y)|dy. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f23cea1b7b2ccbc661ec6890b82e90b3_l3.png)
 的积分,利用
的积分,利用 的一致连续性,
的一致连续性,
对于![Rendered by QuickLaTeX.com \[ \int_{|y| < \delta} \leq \sup_{x \in \mathbb{T}}\sup_{|y| < \delta} |f(x - y) - f(x)| \cdot ||K_N||_1 < \epsilon. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-015094855fb2bf7176f9e6bdbc95ba9c_l3.png)
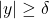 的积分,
的积分,![Rendered by QuickLaTeX.com \[ \int_{|y| \geq \delta} \leq C||f||_\infty \cdot \int_{\delta}^{\frac 12} N^{-1}y^{-2}dy \to 0 \text{ as } N \to \infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d52ab2ec40c9daab9aee1b400e4d2d41_l3.png)
- 上述证明不能用于
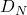 ,原因是
,原因是
因此,我们需要提高![Rendered by QuickLaTeX.com \[ ||D_N||_1 \geq C\ln N \to +\infty \text{ as } N \to \infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8ffb840c281e8fa4dd6c2b09e7f350b3_l3.png)
 的正则性
的正则性
- 注意到
- 如果
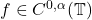 ,
,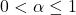 ,那么
,那么![Rendered by QuickLaTeX.com \[ ||D_N * f - f||_\infty \to 0 \text{ as } N \to \infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-91d6905db73a43f3ee7858d00bd03857_l3.png)
- 首先,将
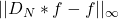 转换为
转换为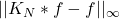 。由于
。由于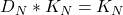 ,故
,故![Rendered by QuickLaTeX.com \[ D_N * f - f = (D_N * f - D_N * K_N * f) + (K_N * f - f), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-653375add88edba9886f9c69ba4acdb1_l3.png)
![Rendered by QuickLaTeX.com \[ ||D_N * f - f||_\infty \leq (|D_N||_1 + 1)||K_N * f - f||_\infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fc6ee14a3024ec66a98ef8ec69f89522_l3.png)
- 然后,更加精细地控制
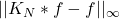 。利用
。利用 的Hölder连续性,
的Hölder连续性,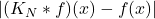 可以被如下积分控制
可以被如下积分控制
而积分的结果可以被![Rendered by QuickLaTeX.com \[ C\int_0^{\frac 1N} [f]_\alpha y^\alpha \cdot Ndy + C\int_{\frac 1N}^{\frac 12} [f]_\alpha y^\alpha \cdot N^{-1}y^{-2}dy, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3c4b7dc5b1db91e2695ec4a24ea3105c_l3.png)
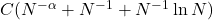 控制(需要注意
控制(需要注意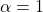 的情形)。因此,当
的情形)。因此,当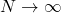 时,
时,![Rendered by QuickLaTeX.com \[ ||D_N * f - f||_\infty \leq C(\ln N + 1)(N^{-\alpha} + N^{-1} + N^{-1}\ln N) \to 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f1269639fe4c8acc9854b98ac1e298e3_l3.png)
- 首先,将