从三角形到单纯形
- 由三角剖分的算法可知,我们可以将复杂的多边形,剖分为简单的三角形
- 点由1个顶点确定,线段由2个顶点确定,三角形由3个顶点确定,四面体由4个顶点确定。一般地,
 -单纯形由
-单纯形由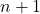 个顶点
个顶点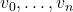 确定,记为
确定,记为![Rendered by QuickLaTeX.com \[ [v_0, \ldots, v_n]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ce48b940563e365900fb2f9877b6dbf8_l3.png)
- 对于三角形
![Rendered by QuickLaTeX.com [v_0, v_1, v_2]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-639d70949a7ee70d0a623e1cb2137b02_l3.png) ,位于线段
,位于线段![Rendered by QuickLaTeX.com [v_0, v_1]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ea910273ac236afc0436f63bd4911b15_l3.png) 上的点可以表示为
上的点可以表示为
这里,系数相加为1的线性组合,称为仿射组合(对应于直线);系数相加为1,并且系数位于0、1之间的线性组合,称为凸组合(对应于线段)![Rendered by QuickLaTeX.com \[ v_0 + \lambda(v_1 - v_0) = (1 - \lambda)v_0 + \lambda v_1,\; \lambda \in [0, 1]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fab8a04de7db969bbe739fc2def3a3a4_l3.png)
- 为了构成一个三角形,任意一个顶点不能等于其他顶点的仿射组合,这称为仿射无关,它可以描述为
因此,![Rendered by QuickLaTeX.com \[ \sum_i \lambda_iv_i = 0,\; \sum_i \lambda_i = 0 \Rightarrow \lambda_i = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e7ac829141c4f46a6f407e0bdf8e5977_l3.png)
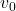 、
、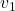 、
、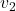 仿射无关,等价于
仿射无关,等价于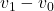 、
、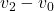 线性无关。进一步,类似于
线性无关。进一步,类似于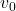 、
、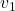 的凸组合构成线段,
的凸组合构成线段,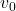 、
、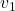 、
、 的凸组合构成三角形
的凸组合构成三角形
- 对于三角形
- 通常,我们需要固定一个标准
 -单形。比如,
-单形。比如, 上的标准单位正交基为
上的标准单位正交基为
它们的仿射组合构成平面,它们的凸组合构成平面上的三角形![Rendered by QuickLaTeX.com \[ e_0 = (1, 0, 0),\; e_1 = (0, 1, 0),\; e_2 = (0, 0, 1). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-09fdbdbe59e749dd809a696384eeaa0c_l3.png)
一般地,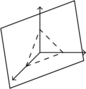
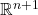 上的标准单位正交基为
上的标准单位正交基为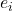 ,
,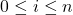 。那么,标准
。那么,标准 -单形为
-单形为![Rendered by QuickLaTeX.com \[ \Delta^n = [e_0, \ldots, e_n]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f1513db73418d211004c305a8794def4_l3.png)
- 在固定了一个标准
 -单形之后,任意一个
-单形之后,任意一个 -单纯形都与之同胚,
-单纯形都与之同胚,
其中,![Rendered by QuickLaTeX.com \[ [v_0, \ldots, v_n] \to [e_0, \ldots, e_n],\; \sum_i \lambda_iv_i \mapsto \sum_i \lambda_ie_i, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5abca44af03d5904586351ecec7778a0_l3.png)
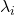 称为重心坐标
称为重心坐标 - 单纯复形
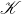 是一族单纯形
是一族单纯形
- 如果
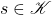 ,那么
,那么 的面
的面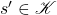
- 如果
 、
、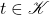 ,那么
,那么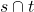 为空集,或者为
为空集,或者为 、
、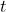 的面
的面
- 如果
三角剖分、多面体细分
- 点位形(Point Configuration)为
其中,![Rendered by QuickLaTeX.com \[ A = \{ a_1, \ldots, a_n \}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b3bc857c9ac35bcbbd8a4940325e16ec_l3.png)
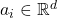 可以是重合的点
可以是重合的点 - 三角剖分(Triangulation)为一个单纯复形
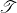
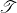 的顶点为
的顶点为 ,即
,即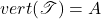
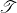 的几何实现为
的几何实现为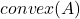 ,即
,即