域扩张的定义
- 关于一般的域上的线性空间,可参见数值线性代数
- 如果
 为
为 的子域,那么
的子域,那么 称为
称为 的扩张。因为
的扩张。因为 是一个
是一个 -线性空间,所以我们可以定义
-线性空间,所以我们可以定义 在
在 上的次数为
上的次数为![Rendered by QuickLaTeX.com \[ [L : K] = dim_KL. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0ccade3723a004f6b3cf9a80d02bc3a8_l3.png)
- 我们有
设![Rendered by QuickLaTeX.com \[ [M : K] = [M : L][L : K]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4751c3b8f0ca227de19802bbf13d871e_l3.png)
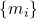 为
为 的
的 -基底,
-基底,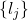 为
为 的
的 -基底。我们只需证明
-基底。我们只需证明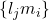 为
为 的
的 -基底
-基底
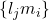 是
是 -线性无关的。原因是
-线性无关的。原因是![Rendered by QuickLaTeX.com \[ \sum_{i, j} k_{ij}l_jm_i = 0,\; k_{ij} \in K \Rightarrow \sum_{j} k_{ij}l_j = 0,\; k_{ij} = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1c3de21b690392f0e5862574e31ed8a5_l3.png)
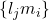 可以生成
可以生成 。原因是对任意
。原因是对任意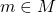 ,
,![Rendered by QuickLaTeX.com \[ m = \sum_i l_i'm_i = \sum_{i, j} k_{ij}l_jm_i,\; l_i' \in L,\; k_{ij} \in K. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-78c33f62cee90dc2cbd4fc8542b38aa7_l3.png)
代数元素
- 如果
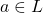 为
为![Rendered by QuickLaTeX.com K[X]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5bb7eb3c66aa1f07f755605c74d2291b_l3.png) 中某个非零多项式的根,那么
中某个非零多项式的根,那么 称为
称为 上的代数元素
上的代数元素 - 极小多项式
- 定义
那么,![Rendered by QuickLaTeX.com \[ I = \{ P \in K[X] : P(a) = 0 \}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-29680f1c8f0436dc0cb89b6db3f32e17_l3.png)
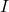 为非零理想
为非零理想 - 取
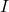 中一个次数最低的非零多项式
中一个次数最低的非零多项式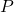 。因为
。因为![Rendered by QuickLaTeX.com K[X]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5bb7eb3c66aa1f07f755605c74d2291b_l3.png) 可以进行带余除法,所以
可以进行带余除法,所以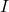 中的多项式都可以被
中的多项式都可以被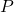 整除。将
整除。将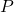 化为首一多项式,那么
化为首一多项式,那么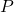 还是唯一的
还是唯一的 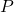 称为
称为 的极小多项式,
的极小多项式,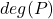 称为
称为 在
在 上的次数
上的次数
- 定义
- 极小多项式的性质
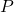 是不可约的,否则
是不可约的,否则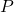 可以分解出一个次数更低的多项式
可以分解出一个次数更低的多项式- 如果
![Rendered by QuickLaTeX.com Q \in K[X]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-847133f5fbe0c59a9e18fe82d40262f8_l3.png) ,
,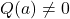 ,那么
,那么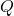 不能被
不能被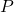 整除,从而
整除,从而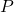 、
、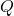 互素。由Bézout定理,存在
互素。由Bézout定理,存在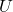 、
、![Rendered by QuickLaTeX.com V \in K[X]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f3346ca66c5db4e23869499332f69513_l3.png) ,使得
,使得
因此,![Rendered by QuickLaTeX.com \[ PU + QV = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-627db2a5a96e54f6c2066dcd4ea2f9f8_l3.png)
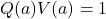 ,
,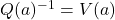
- 单个代数元素
 生成的扩张
生成的扩张
- 多项式环
![Rendered by QuickLaTeX.com K[X]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5bb7eb3c66aa1f07f755605c74d2291b_l3.png) 对应于
对应于![Rendered by QuickLaTeX.com K[a]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bc87e50c2ea29bf0adb5319f14805bbb_l3.png) ,分式域
,分式域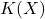 对应于
对应于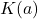 。由极小多项式的性质,
。由极小多项式的性质,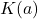 中的分母(不为零)在
中的分母(不为零)在![Rendered by QuickLaTeX.com K[a]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bc87e50c2ea29bf0adb5319f14805bbb_l3.png) 中是可逆的,所以
中是可逆的,所以![Rendered by QuickLaTeX.com K[a] = K(a)](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-840a0434117544af39f876a0e146505e_l3.png)
- 我们有
设![Rendered by QuickLaTeX.com \[ [K[a] : K] = deg(P). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-df4ed70f66421f57fb6740b37cd5c55e_l3.png)
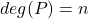
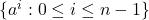 是
是 -线性无关的。否则,
-线性无关的。否则, 为次数更低的非零多项式的零点,
为次数更低的非零多项式的零点,![Rendered by QuickLaTeX.com \[ \sum_{i = 0}^{n - 1} k_ia^i = 0,\; k_i \in K. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7e868317f59073a9caa2aac65f157af6_l3.png)
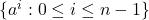 可以生成
可以生成![Rendered by QuickLaTeX.com K[a]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bc87e50c2ea29bf0adb5319f14805bbb_l3.png) 。原因是对任意
。原因是对任意![Rendered by QuickLaTeX.com S(a) \in K[a]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c8118802c880b8b7d9f0b0465d4a31d9_l3.png) ,
,![Rendered by QuickLaTeX.com S \in K[X]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7d86a2c3451b735af000d10aaca50ef0_l3.png) ,进行带余除法,
,进行带余除法,
那么,![Rendered by QuickLaTeX.com \[ S = PT + R,\; 0 \leq deg(R) < n. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-33063e6b3e231f3fd3fe7c4a5896e7f6_l3.png)
![Rendered by QuickLaTeX.com \[ S(a) = R(a) = \sum_{i = 0}^{n - 1} k_ia^i,\; k_i \in K. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-caafa387ad3798d85afc1822a1d76479_l3.png)
- 多项式环
- 多个代数元素
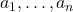 生成的扩张
生成的扩张
- 多项式环
![Rendered by QuickLaTeX.com K[X_1, \ldots, X_n]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-24374cf605182c877f41aa86d1d48018_l3.png) 对应于
对应于![Rendered by QuickLaTeX.com K[a_1, \ldots, a_n]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-42d646cafc40354e5cea2a95855b4077_l3.png) ,分式域
,分式域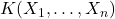 对应于
对应于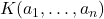
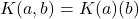 ,原因是分式域具有极小性
,原因是分式域具有极小性![Rendered by QuickLaTeX.com \[ K, a, b \subset K(a)(b) \Rightarrow K(a, b) \subset K(a)(b), \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-861b665176fe318b8569f838229a8d1a_l3.png)
由数学归纳法,![Rendered by QuickLaTeX.com \[ K(a), b \subset K(a, b) \Rightarrow K(a)(b) \subset K(a, b). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f580d794ff0e3d99d5236261cac910b3_l3.png)
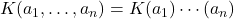
![Rendered by QuickLaTeX.com K[a, b] = K[a][b]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0a5d39d1e525cdbba73161c4ae4bb75f_l3.png) ,原因是
,原因是![Rendered by QuickLaTeX.com K[a, b]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d12d88cdbc2d3dff33f4aff2bcdb6837_l3.png) 中的多项式可以视为关于
中的多项式可以视为关于 的多项式,其系数为
的多项式,其系数为 的多项式。由数学归纳法,
的多项式。由数学归纳法,![Rendered by QuickLaTeX.com K[a_1, \ldots, a_n] = K[a_1]\cdots[a_n]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-eeac081144c7336c03be1bfc655b8de8_l3.png)
- 由单个代数元素的结果,
![Rendered by QuickLaTeX.com K[a_1, \ldots, a_n] = K(a_1, \ldots, a_n)](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-44f1768723963ea9a964baa5628af63e_l3.png)
- 多项式环
代数扩张
- 如果
 中的元素都是
中的元素都是 上的代数元素,那么
上的代数元素,那么 称为
称为 上的代数扩张
上的代数扩张 - 如果
![Rendered by QuickLaTeX.com [L : K]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-91d5750b9efee95e81ca546909527d55_l3.png) 有限,那么
有限,那么 为
为 上的代数扩张
上的代数扩张
- 设
![Rendered by QuickLaTeX.com [L : K] = n](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7650624c7520f97784bf68a4acb89cb4_l3.png) 。那么,对任意
。那么,对任意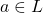 ,
,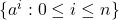 包含
包含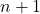 个元素,从而是
个元素,从而是 -线性相关的。因此,
-线性相关的。因此, 为非零多项式的零点,
为非零多项式的零点,![Rendered by QuickLaTeX.com \[ \sum_{i = 0}^n k_ia^i = 0,\; k_i \in K. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-25ad0315311658b9457072c63a7a56d0_l3.png)
- 设
- 多个代数元素
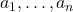 生成的扩张是代数扩张
生成的扩张是代数扩张
- 注意到
单个代数元素生成的扩张满足![Rendered by QuickLaTeX.com \[ [K[a_1, \ldots, a_n] : K] = \prod_{i = 1}^n [K[a_1, \ldots, a_i] : K[a_1, \ldots, a_{i - 1}]]. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-dcc0c107018fa2c315d7bffa617fcd6c_l3.png)
其中,![Rendered by QuickLaTeX.com \[ [K[a_1, \ldots, a_i] : K[a_1, \ldots, a_{i - 1}]] \leq [K[a_i] : K] = deg(P_i). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a1ef319bb024826c84c1f1fb2904db89_l3.png)
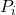 为
为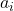 在
在 上的极小多项式。因此,
上的极小多项式。因此,![Rendered by QuickLaTeX.com [K[a_1, \ldots, a_n] : K]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a1beb044d0a7bf6686354f5bbf539276_l3.png) 有限,
有限,![Rendered by QuickLaTeX.com K[a_1, \ldots, a_n]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-42d646cafc40354e5cea2a95855b4077_l3.png) 为
为 上的代数扩张
上的代数扩张
- 注意到
- 由此可知,如果
 、
、 为
为 上的代数元素,那么
上的代数元素,那么![Rendered by QuickLaTeX.com K[a, b]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d12d88cdbc2d3dff33f4aff2bcdb6837_l3.png) 为
为 上的代数扩张。因此
上的代数扩张。因此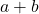 、
、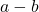 、
、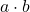 、
、![Rendered by QuickLaTeX.com a / b \in K[a, b]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5be96b9aa2ff0ddbbbeeb0c135c056a2_l3.png) 都为
都为 上的代数元素,即代数元素关于四则运算封闭
上的代数元素,即代数元素关于四则运算封闭
代数闭包
- 在上面的讨论中,我们淡化了
 的作用。我们可以得到,对于
的作用。我们可以得到,对于 ,
, 上包含在
上包含在 中的代数元素构成一个域,但是
中的代数元素构成一个域,但是 可能太小,不足以找到
可能太小,不足以找到 上所有的代数元素
上所有的代数元素 - 比如对于有理数域和实数域
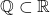 ,
,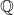 上包含在
上包含在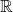 中的代数元素构成一个域
中的代数元素构成一个域 。
。 可以找到类似于
可以找到类似于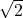 这样的代数元素(
这样的代数元素(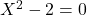 ),但是不足以找到类似于
),但是不足以找到类似于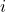 这样的代数元素(
这样的代数元素(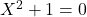 )
) - 一种办法是使用更大的复数域
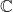 。由复数域上的分析中的代数基本定理,在
。由复数域上的分析中的代数基本定理,在 中可以找到
中可以找到![Rendered by QuickLaTeX.com \mathbb{C}[X]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-62f93f65b4a4ebe04a79508973795006_l3.png) 中多项式的所有零点,具有这种性质的域称为代数封闭的域。此时,
中多项式的所有零点,具有这种性质的域称为代数封闭的域。此时, 上包含在
上包含在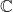 中的代数元素构成一个域
中的代数元素构成一个域 。我们有
。我们有
其中,![Rendered by QuickLaTeX.com \[ \mathbb{Q} \subset \mathbb{Q}_1 \subset \overline{\mathbb{Q}} \subset \mathbb{C}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-944399db2d7fffaea19babe9fde46ef2_l3.png)
 是代数扩张,但不是代数封闭的;
是代数扩张,但不是代数封闭的;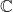 是代数封闭的,但不是代数扩张(比如存在超越数)
是代数封闭的,但不是代数扩张(比如存在超越数) - 只有
 既是代数扩张,又是代数封闭的。由定义可知,
既是代数扩张,又是代数封闭的。由定义可知, 是代数扩张。对于代数封闭,设
是代数扩张。对于代数封闭,设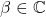 为如下多项式的零点,
为如下多项式的零点,
由上面的笔记,令![Rendered by QuickLaTeX.com \[ X^n + \alpha_{n - 1}X^{n - 1} + \cdots \alpha_0,\; \alpha_i \in \overline{\mathbb{Q}}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0c0673c9a0f5c8b4f7fdcdd31e232c9b_l3.png)
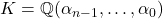 ,那么,
,那么,
因此,![Rendered by QuickLaTeX.com \[ [K(\beta) : K] \leq n,\; [K : \mathbb{Q}] < \infty. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4bb23f2a69bcc9887fc624d4533f4fef_l3.png)
即![Rendered by QuickLaTeX.com \[ [\mathbb{Q}(\beta) : \mathbb{Q}] \leq [K(\beta) : \mathbb{Q}] = [K(\beta) : K][K : \mathbb{Q}] < \infty, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-54d7133e918f589736b6dd806d1b83dc_l3.png)
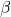 是
是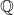 上的代数元素,
上的代数元素,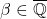
- 对于一般的域
 ,代数封闭的代数扩张
,代数封闭的代数扩张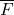 称为代数闭包。代数闭包的存在性不是一个平凡的结果,不过我们可以先使用它
称为代数闭包。代数闭包的存在性不是一个平凡的结果,不过我们可以先使用它