系统响应
- 关于确定信号的时频分析,可参见频率响应和采样率
- 确定信号通过线性时不变系统
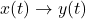 ,系统响应为
,系统响应为
随机信号通过线性时不变系统![Rendered by QuickLaTeX.com \[ y(t) = (x * h)(t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8322671ba589d9358c3abf9c67be1a6c_l3.png)
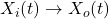 ,系统响应为
,系统响应为
这里,![Rendered by QuickLaTeX.com \[ X_o(t) = (X_i * h)(t). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-153f66898b504640070c4bb8ef91ff4d_l3.png)
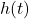 为脉冲信号
为脉冲信号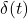 的系统响应,
的系统响应,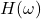 为相应的频率响应
为相应的频率响应 - 对于随机信号,我们考虑平稳过程
- 均值
![Rendered by QuickLaTeX.com \[ \mu_o(t) = \mathbb{E}[X_o(t)] = \int_{-\infty}^{+\infty} \mathbb{E}[X_i(t - \tau)] \cdot h(\tau)d\tau = \mu_i(0)H(0). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-486cdf7ab2991ebc65a5bfdcf44ef798_l3.png)
- 自相关函数
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} R_o(\tau) &= \mathbb{E}[X_o(t + \tau)X_o(t)] \\ &= \mathbb{E}\bigg[\int_{-\infty}^{+\infty} X_i(t + \tau - \tau_1)h(\tau_1)d\tau_1\int_{-\infty}^{+\infty} X_i(t - \tau_2)h(\tau_2)d\tau_2\bigg] \\ &= \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} \mathbb{E}[X_i(t + \tau - \tau_1)X_i(t - \tau_2)] \cdot h(\tau_1)h(\tau_2)d\tau_1d\tau_2 \\ &= \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} R_i(\tau - \tau_1 + \tau_2) \cdot h(\tau_1)h(\tau_2)d\tau_1d\tau_2. \end{split}\end{equation*}](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f9e7776be8332f2303a65ffb0f875b1e_l3.png)
- 功率谱密度
积分的结果为![Rendered by QuickLaTeX.com \[ S_o(\omega) = \int_{-\infty}^{+\infty} R_o(\tau)e^{-j\omega\tau}d\tau. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-68e4aa2ac3e23233890bdc05545c6821_l3.png)
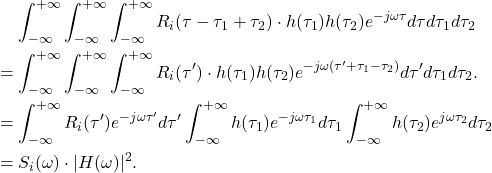
- 均值
噪声通过系统
- 白噪声
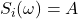 通过低通滤波器
通过低通滤波器
可得带宽有限的白噪声![Rendered by QuickLaTeX.com \[ H(\omega) = 1_{[-2\pi W, 2\pi W]}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1e3e2b559d739f9cd7732a6a3910bdbc_l3.png)
![Rendered by QuickLaTeX.com \[ S_o(\omega) = A1_{[-2\pi W, 2\pi W]}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-4dd7ac760845e824014a2b7fb5a793b2_l3.png)
- 如果噪声的频谱位于
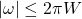 ,那么通过低通滤波器之后,功率谱密度保持不变
,那么通过低通滤波器之后,功率谱密度保持不变
在时域上,与类似于如下的sinc函数卷积之后![Rendered by QuickLaTeX.com \[ S_o(\omega) = S_i(\omega) \cdot 1_{[-2\pi W, 2\pi W]} = S_i(\omega). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a69450172b136d32a163eecd1551b5ed_l3.png)
自相关函数保持不变![Rendered by QuickLaTeX.com \[ sinc(x) = \frac{sin(x)}{x}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0767540c5538d1c3daf31014fa5f262f_l3.png)
![Rendered by QuickLaTeX.com \[ R_o(\tau) = R_i(\tau) * \bigg[\frac{\sin(2\pi W\tau)}{\pi\tau}\bigg] = R_i(\tau). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a29674d60fc7fe9c1e64015280702129_l3.png)
- 在Fourier级数的收敛性中,Dirichlet核是sinc函数的离散版本,
Fejér核![Rendered by QuickLaTeX.com \[ D_N(x) = \frac{\sin[(2N + 1)\pi x]}{\sin(\pi x)}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7f7cea1c5e8ad1600b146770e281bb70_l3.png)
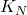 的频谱位于
的频谱位于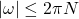 。在时域上,与Dirichlet核卷积之后,Fejér核保持不变
。在时域上,与Dirichlet核卷积之后,Fejér核保持不变![Rendered by QuickLaTeX.com \[ D_N * K_N = K_N. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-2e8d706c2be396b5c544a2e8ed61aa7b_l3.png)