隐函数定理
- 我们利用逆映射定理,得到隐函数定理
- 逆映射定理求解显式方程
![Rendered by QuickLaTeX.com \[ y = f(x). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-20282ec1fc97a6fcf8e7739fd1f958c9_l3.png)
- 隐函数定理求解隐式方程
![Rendered by QuickLaTeX.com \[ f(x, y) = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-cbb483e0fd0a663e7e2bf1830aebd0de_l3.png)
- 逆映射定理求解显式方程
- 设
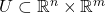 为开集,
为开集,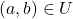
- (隐函数定理)如果
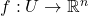 为
为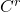 映射,
映射,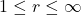 ,如下的隐式方程在
,如下的隐式方程在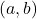 处成立
处成立
并且![Rendered by QuickLaTeX.com \[ f(x, y) = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-eb557ae79ffbe9a69bf47d469fe2b923_l3.png)
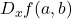 可逆,那么隐式方程在
可逆,那么隐式方程在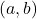 处局部有
处局部有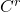 显式解,
显式解,
显式解![Rendered by QuickLaTeX.com \[ f(x, y) = 0 \Rightarrow x = g(y). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-598cf7699b267b9a029b685a7e55fd98_l3.png)
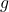 是唯一的,并且隐函数的求导法则为
是唯一的,并且隐函数的求导法则为![Rendered by QuickLaTeX.com \[ Dg(b) = -D_xf(a, b)^{-1} \cdot D_yf(a, b). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-025970ffbb8ea21122756f9d738952d5_l3.png)
- 我们需要寻找
 、
、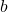 的开邻域
的开邻域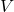 、
、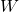 ,以及
,以及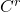 映射
映射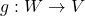 ,使得
,使得![Rendered by QuickLaTeX.com \[ V \times W \subset U,\; f(g(y), y) = 0,\; y \in W. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a933650e0f020b0fe6817482f23932a4_l3.png)
- 令
那么,![Rendered by QuickLaTeX.com \[ F: (x, y) \mapsto (f(x, y), y),\; (x, y) \in U. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-bc1bf993b5de8e471e99dcc803a30d1d_l3.png)
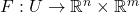 为
为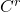 映射,并且
映射,并且
因为![Rendered by QuickLaTeX.com \[ F(a, b) = (0, b),\; DF = \begin{bmatrix}D_xf & D_yf \\ 0 & I_m\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-fa8f2fad6c74e8f3dc17bb55a747c784_l3.png)
所以由逆映射定理可知,存在![Rendered by QuickLaTeX.com \[ \det[DF(a, b)] = \det[D_xf(a, b)] \neq 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a7e0eed27117d877e9ff6bc2563745f5_l3.png)
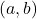 、
、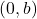 的开邻域
的开邻域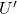 、
、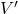 ,使得
,使得
为![Rendered by QuickLaTeX.com \[ F|_{U'}: U' \to V' \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f0d7f25619defdaa350e34a615a856a7_l3.png)
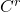 微分同胚
微分同胚 - 取
 、
、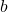 的开邻域
的开邻域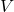 、
、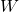 ,使得
,使得
对于![Rendered by QuickLaTeX.com \[ V \times W \subset U',\; \{0\} \times W \subset V'. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-8bbac7c112a40baa3ed48be3f1d4ffe8_l3.png)
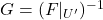 ,我们记
,我们记
由下式可知,![Rendered by QuickLaTeX.com \[ G: (0, y) \mapsto (g(y), y),\; y \in W. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d7641b73e32fb42f9c00193a7c93ec38_l3.png)
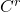 显式解为
显式解为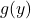 ,
,
同时,由于![Rendered by QuickLaTeX.com \[ (0, y) = F \circ G(0, y) = (f(g(y), y), y),\; y \in W. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-ec88a47107b1d539247a58682842f56b_l3.png)
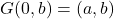 ,故
,故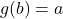 。我们可以进一步取
。我们可以进一步取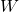 ,使得
,使得 。因此,我们找到了想要的
。因此,我们找到了想要的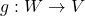
- 令
- 对于
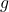 的唯一性,如果
的唯一性,如果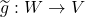 为另一个
为另一个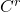 映射,满足
映射,满足
那么,![Rendered by QuickLaTeX.com \[ f(\widetilde{g}(y), y) = 0, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-b89e1567401916c27e3fcb7c64d2ced3_l3.png)
由于![Rendered by QuickLaTeX.com \[ F(\widetilde{g}(y), y) = (0, y) = F(g(y), y). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e9336492c2006b2279cae1280f2bb2ac_l3.png)
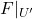 为单射,故
为单射,故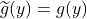
- 对于隐函数的求导法则,将
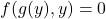 在
在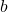 处对
处对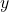 求导,
求导,
因此,![Rendered by QuickLaTeX.com \[ 0 = Df(a, b) \cdot \begin{bmatrix} Dg(b) \\ I_m \end{bmatrix} = D_xf(a, b) \cdot Dg(b) + D_yf(a, b). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c64b810ca8e622958b27633c980afb2a_l3.png)
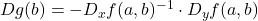
- 我们需要寻找
从局部到整体
- 在计算机图形学中,
 中的曲面
中的曲面 可以用隐式方程来描述。比如,2维球面
可以用隐式方程来描述。比如,2维球面 为
为![Rendered by QuickLaTeX.com \[ f(x, y, z) = x^2 + y^2 + z^2 - 1 = 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-616274e48fd41d66326923f349601a42_l3.png)
- (局部坐标邻域)对于
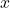 坐标,我们定义局部坐标邻域
坐标,我们定义局部坐标邻域
对于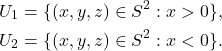
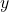 坐标,我们有
坐标,我们有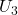 、
、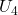 ;对于
;对于 坐标,我们有
坐标,我们有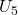 、
、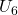 。因此,
。因此,![Rendered by QuickLaTeX.com \[ S^2 = \cup_i U_i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5706df9a5a775de9307e4b406bf10842_l3.png)
- (局部坐标映射)注意到
由隐函数定理,我们可以在![Rendered by QuickLaTeX.com \[ D_xf(x, y, z) = 2x \neq 0,\; (x, y, z) \in U_1, U_2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3c6ba1ff2e4e0d75979cb75c4a1438ab_l3.png)
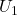 、
、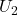 上求解隐式方程,即
上求解隐式方程,即
因为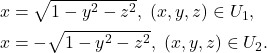
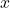 坐标是冗余的,所以2维坐标
坐标是冗余的,所以2维坐标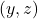 即可在局部描述
即可在局部描述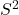 。局部坐标映射为
。局部坐标映射为
对于![Rendered by QuickLaTeX.com \[ \varphi_i: U_i \subset S^2 \to \varphi_i(U_i) \subset \mathbb{R}^2,\; (x, y, z) \mapsto (y, z),\; i = 1, 2. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-9907f4d5d8ddc7c49224a19a436e5009_l3.png)
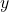 坐标,我们有
坐标,我们有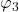 、
、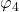 ;对于
;对于 坐标,我们有
坐标,我们有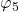 、
、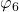
- (转移映射)尽管单个坐标卡
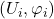 只能在局部描述
只能在局部描述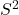 ,然而整个坐标图册
,然而整个坐标图册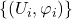 可以在整体描述
可以在整体描述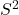
- 坐标图册源于地图学。世界地图(基本上)给出了
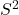 的坐标图册——在低纬度取一个坐标卡、在北极、南极附近分别取一个坐标卡,然后将它们粘贴在一起
的坐标图册——在低纬度取一个坐标卡、在北极、南极附近分别取一个坐标卡,然后将它们粘贴在一起 - 粘贴即坐标卡之间的对应关系,它可以用转移映射来描述。比如,从
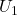 到
到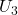 的转移映射为
的转移映射为
注意,![Rendered by QuickLaTeX.com \[ \varphi_3 \circ \varphi_1^{-1}(y, z) = \varphi_3(\sqrt{1 - y^2 - z^2}, y, z) = (\sqrt{1 - y^2 - z^2}, z). \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-22619bdbc9c51fe18145cf3a36eb3e3a_l3.png)
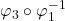 为
为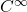 映射,其他的转移映射也是类似的。因此,我们称
映射,其他的转移映射也是类似的。因此,我们称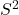 为2维
为2维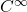 流形(Manifold)
流形(Manifold)
- 坐标图册源于地图学。世界地图(基本上)给出了
在不同的域上求解方程
- 隐式方程
还是一个代数方程。如果求解代数方程,那么我们可以得到代数簇(Algebraic Variety)![Rendered by QuickLaTeX.com \[ f(x, y, z) = x^2 + y^2 + z^2 - 1 = 0 \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-77a3b9c1234b4bc23f4bd3937ddb38b2_l3.png)
- 我们也可以在实数域
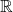 之外求解代数方程。如果在复数域
之外求解代数方程。如果在复数域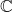 上求解代数方程,那么我们可以得到复代数簇。进一步,如果代数方程满足隐函数定理中的非退化条件,那么我们可以得到复流形
上求解代数方程,那么我们可以得到复代数簇。进一步,如果代数方程满足隐函数定理中的非退化条件,那么我们可以得到复流形 - 在计算理论中(比如Hilbert第10问题),我们考虑整数
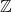 上的代数方程,即Diophantus方程。如果求解Diophantus方程,那么我们可以得到有理数域
上的代数方程,即Diophantus方程。如果求解Diophantus方程,那么我们可以得到有理数域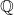 上的代数簇
上的代数簇 - 在编码理论中,我们考虑有限域
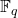 上的代数方程。如果求解有限域
上的代数方程。如果求解有限域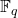 上的代数方程,那么我们可以得到有限域
上的代数方程,那么我们可以得到有限域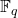 上的代数簇
上的代数簇 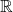 、
、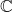 对应于几何,
对应于几何,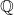 、
、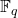 对应于算术
对应于算术
- 如果在
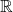 、
、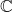 上建立实、复分析,那么我们可以得到微分流形、复流形。这对应于微分几何、复几何
上建立实、复分析,那么我们可以得到微分流形、复流形。这对应于微分几何、复几何 - 然而,在
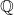 、
、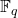 上,我们难以建立分析。如果只利用代数,将几何移植到算术上,那么我们可以得到概形(Scheme)。这对应于代数几何、算术几何
上,我们难以建立分析。如果只利用代数,将几何移植到算术上,那么我们可以得到概形(Scheme)。这对应于代数几何、算术几何
- 如果在