四元数的定义
- 关于伴随矩阵、行列式,可参见从线性方程出发
- 四元数的集合为
![Rendered by QuickLaTeX.com \[ \mathbb{H} = \bigg\{ \begin{bmatrix}z & -w \\ \overline{w} & \overline{z}\end{bmatrix} \in M_2(\mathbb{C}) : z, w \in \mathbb{C} \bigg\}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-29d8ff457b1ed9a33b7909c2b8fb3dea_l3.png)
- 对任意
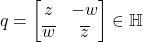 ,它的共轭为
,它的共轭为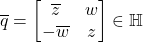 ,它的模长为
,它的模长为
也就是说,四元数的共轭对应于伴随矩阵,模长的平方对应于行列式。由伴随矩阵、行列式的性质,![Rendered by QuickLaTeX.com \[ |q| = \sqrt{\det\begin{bmatrix}z & -w \\ \overline{w} & \overline{z}\end{bmatrix}} = \sqrt{|z|^2 + |w|^2}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-947c352bc9664c75dff219094e42437d_l3.png)
![Rendered by QuickLaTeX.com \[ q\overline{q} = \overline{q}q = |q|^2,\; q \in \mathbb{H}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0a76861a529c612f6b46812550be6032_l3.png)
![Rendered by QuickLaTeX.com \[ |q_1q_2| = |q_1||q_2|,\; q_1, q_2 \in \mathbb{H}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-e9d5a087a10e011ca7cbc81588f8b5ca_l3.png)
 为有单位元素的、结合的
为有单位元素的、结合的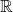 -代数
-代数
- 由数值线性代数可知,
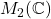 为有单位元素的、结合的
为有单位元素的、结合的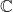 -代数。然而,我们只能得到
-代数。然而,我们只能得到 为
为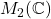 的
的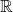 -子代数
-子代数 - 首先,
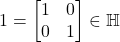 。其次,对任意
。其次,对任意
我们有![Rendered by QuickLaTeX.com \[ $\lambda_1, \lambda_2 \in \mathbb{R},\; q_1 = \begin{bmatrix}z_1 & -w_1 \\ \overline{w_1} & \overline{z_1}\end{bmatrix},\; q_2 = \begin{bmatrix}z_2 & -w_2 \\ \overline{w_2} & \overline{z_2}\end{bmatrix} \in \mathbb{H}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-211c816f148490ea85fc717603e30faf_l3.png)
![Rendered by QuickLaTeX.com \[ \lambda_1q_1 + \lambda_2q_2 = \begin{bmatrix}\lambda_1z_1 + \lambda_2z_2 & -(\lambda_1w_1 + \lambda_2w_2) \\ \overline{\lambda_1w_1 + \lambda_2w_2} & \overline{\lambda_1z_1 + \lambda_2z_2}\end{bmatrix} \in \mathbb{H}, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-c84519728a11d406529b762489d11798_l3.png)
注意,在第一个等式中,![Rendered by QuickLaTeX.com \[ q_1q_2 = \begin{bmatrix}z_1z_2 - w_1\overline{w_2} & -(z_1w_2 + w_1\overline{z_2}) \\ \overline{z_1w_2 + w_1\overline{z_2}} & \overline{z_1z_2 - w_1\overline{w_2}}\end{bmatrix} \in \mathbb{H}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5b0282cdb710f9083f4139eb8f3db3eb_l3.png)
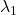 、
、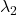 必须为实数,所以
必须为实数,所以 是
是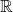 -代数,但不是
-代数,但不是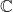 -代数
-代数
- 由数值线性代数可知,
 为可除代数
为可除代数
- 对任意
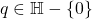 ,我们有
,我们有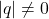 。因此,
。因此,
注意,![Rendered by QuickLaTeX.com \[ q^{-1} = \frac{1}{|q|^2}\overline{q}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-da3860eb78cdd605fd7e9481035f0ee3_l3.png)
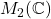 不是可除代数(存在非零、不可逆的矩阵),但
不是可除代数(存在非零、不可逆的矩阵),但 是可除代数
是可除代数
- 对任意
四元数的另一种定义
- 设
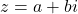 、
、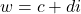 ,
, 、
、 、
、 、
、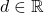 。那么,
。那么,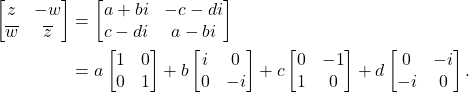
- 由上述可知,
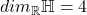 ,并且我们可以将
,并且我们可以将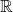 -基底重命名为
-基底重命名为
也就是说,四元数的另一种定义为![Rendered by QuickLaTeX.com \[ \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} \mapsto 1,\; \begin{bmatrix}i & 0 \\ 0 & -i\end{bmatrix} \mapsto i,\; \begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix} \mapsto j,\; \begin{bmatrix}0 & -i \\ -i & 0\end{bmatrix} \mapsto k. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-90f134427ab31b1c08247a3807709882_l3.png)
其乘法结构为![Rendered by QuickLaTeX.com \[ q = a + bi + cj + dk, \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-d813313f6d1dcd4658f28747de7fbcf5_l3.png)
![Rendered by QuickLaTeX.com \[ i^2 = j^2 = k^2 = -1,\; ij = -ji = k,\; ki = -ik = j,\; jk = -kj = i. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-1d0c22f1885b5ff9a9131f9bf2318991_l3.png)
- 对于四元数的共轭,
因此,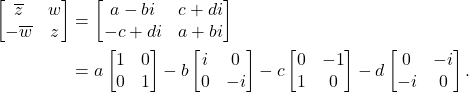
模长为1的四元数
- 模长为1的四元数,两种视角
- 将
 视为
视为
- 模长为1的四元数 –> 3维球面
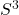
- 模长为1的四元数 –> 3维球面
- 将
 视为
视为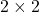 的矩阵
的矩阵
- 模长为1的四元数 –>
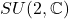
- 模长为1的四元数 –>
- 将
- 对于
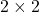 的矩阵,
的矩阵,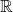 、
、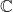 的两种情形是类似的
的两种情形是类似的
- 对于
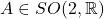 ,我们有
,我们有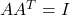 ,
,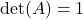 ,即
,即![Rendered by QuickLaTeX.com \[ \begin{bmatrix}a & b \\ c & d\end{bmatrix} \cdot \begin{bmatrix}a & c \\ b & d\end{bmatrix} = \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix},\; ad - bc = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-15671d43ab9391b0c0d7172e745157c0_l3.png)
- 由于
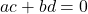 ,故
,故![Rendered by QuickLaTeX.com \[ a = -\frac{bd}{c} \text{ if } c \neq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-86d3119c7c5d1f43b18fcd1cc044f627_l3.png)
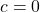 的情形是类似的,我们可以用
的情形是类似的,我们可以用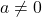 来求解
来求解
- 由于
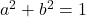 ,
,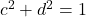 ,故
,故![Rendered by QuickLaTeX.com \[ 1 = \frac{b^2d^2}{c^2} + b^2 = \frac{b^2}{c^2} \Rightarrow b = c\epsilon,\; \epsilon = \pm 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-7fa3b2733632cbf1c6014db72a8e141f_l3.png)
- 由此可知,
取![Rendered by QuickLaTeX.com \[ A = \begin{bmatrix}-d\epsilon & c\epsilon \\ c & d\end{bmatrix},\; \det(A) = -\epsilon. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-0d7c01fd88519daa91fb742c44b5bf38_l3.png)
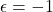 ,
,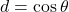 ,
,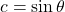 ,可得
,可得
因此,![Rendered by QuickLaTeX.com \[ A = \begin{bmatrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta\end{bmatrix}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-3fec864f333ba18c2f92af87e7527cd3_l3.png)
 为绕原点的旋转,从而
为绕原点的旋转,从而![Rendered by QuickLaTeX.com \[ SO(2, \mathbb{R}) \cong S^1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-a990ae6bde403c8bf2f0e0e49f179c97_l3.png)
- 由于
- 对于
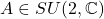 ,我们有
,我们有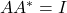 ,
,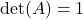 ,即
,即![Rendered by QuickLaTeX.com \[ \begin{bmatrix}a & b \\ c & d\end{bmatrix} \cdot \begin{bmatrix}\overline{a} & \overline{c} \\ \overline{b} & \overline{d}\end{bmatrix} = \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix},\; ad - bc = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f2399358f42f40b5bd93001d7a2de4e1_l3.png)
- 由于
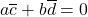 ,故
,故![Rendered by QuickLaTeX.com \[ a = -\frac{b\overline{d}}{\overline{c}} \text{ if } \overline{c} \neq 0. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-5e48e960ec3f53bbce3acceb8a5657d7_l3.png)
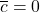 的情形是类似的,我们可以用
的情形是类似的,我们可以用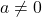 来求解
来求解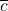
- 由于
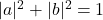 ,
,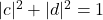 ,故
,故![Rendered by QuickLaTeX.com \[ 1 = \frac{|b|^2|d|^2}{|c|^2} + |b|^2 = \frac{|b|^2}{|c|^2} \Rightarrow b = \overline{c}\epsilon,\; \epsilon = e^{i\theta}. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-72c6fbe26a8ad5eae05dc4cd5ff6cc81_l3.png)
- 由此可知,
取![Rendered by QuickLaTeX.com \[ A = \begin{bmatrix}-\overline{d}\epsilon & \overline{c}\epsilon \\ c & d\end{bmatrix},\; \det(A) = -\epsilon. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-51f53eec31d7fd615cea327d29d24de7_l3.png)
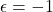 ,
,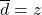 ,
,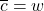 ,可得
,可得
因此,![Rendered by QuickLaTeX.com \[ A = \begin{bmatrix}z & -w \\ \overline{w} & \overline{z}\end{bmatrix},\; |z|^2 + |w|^2 = 1. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-798ccbedb59bdfcb25c32ba608ed2530_l3.png)
 为模长为1的四元数,从而
为模长为1的四元数,从而![Rendered by QuickLaTeX.com \[ SU(2, \mathbb{C}) \cong S^3. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-46f86a415460a4781dcff7baecebd4fb_l3.png)
- 由于
- 对于