道可道,非常道。名可名,非常名。——《老子》
数理逻辑和编程语言
- 关于归纳定义、推理规则,可参见从不动点定理到编程语言
- 在数理逻辑中,我们有字母表(Alphabet);在编程语言中,我们有字符集(Character Set)
- 在数理逻辑中,字母表的元素称为字母(Letter);在编程语言中,字符集的元素称为字符(Character)
- 群论
- 设
 为集合。那么,
为集合。那么, 生成
生成
- 自由半群(Free Semigroup)
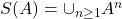
- 自由幺半群(Free Monoid)
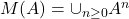 ,它具有单位元素
,它具有单位元素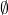
- 自由群(Free Group)
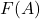 ,它具有逆元素
,它具有逆元素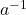 ,
,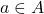
- 自由半群(Free Semigroup)
- 设
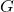 为群
为群
- 由群论的结果可知,对任意映射
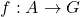 ,存在唯一的自由扩张
,存在唯一的自由扩张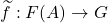 。在Shannon熵中,唯一译码的编码需要使用半群上的自由扩张
。在Shannon熵中,唯一译码的编码需要使用半群上的自由扩张 - 设
 为
为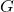 的一个生成元集。那么,含入映射
的一个生成元集。那么,含入映射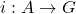 有自由扩张
有自由扩张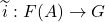 。因为
。因为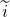 为满同态,所以我们有同构
为满同态,所以我们有同构![Rendered by QuickLaTeX.com \[ F(A) / ker\widetilde{i} \cong G. \]](https://yiming-2023.com/wp-content/ql-cache/quicklatex.com-f136cc6f2b98f731fc71c28f9b2e9196_l3.png)
- 设
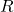 为
为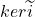 的一个生成元集。那么,我们称字母表
的一个生成元集。那么,我们称字母表 、关系
、关系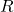 为群
为群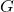 的一个表现,记为
的一个表现,记为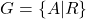 。如果
。如果 、
、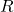 为有限的,那么
为有限的,那么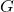 称为有限表现群;如果
称为有限表现群;如果 为有限的,那么
为有限的,那么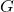 称为有限生成群
称为有限生成群
- 由群论的结果可知,对任意映射
- 设
- 在数理逻辑中,字母表生成字(Word);在编程语言中,字符生成字符串(String)
- 在编码理论中,比如一般线性编码,我们考虑
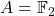 或者
或者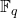 。
。 生成二进制串(Bitstring)或者
生成二进制串(Bitstring)或者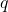 阶串(
阶串(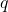 -ary String),它们是机器语言
-ary String),它们是机器语言
- 在编码理论中,比如一般线性编码,我们考虑
- 词法(Lexicon)
- (数理逻辑)表达式(Expression)由字、推理规则归纳定义
- 项(Term),比如Lambda演算的Lambda项
- 公式(Formula),比如命题逻辑(Propositional Logic)的公式
- (编程语言)单词(Token)由字符串、推理规则归纳定义
- 保留字(Reserved Word),比如由公理定义
- 正则表达式(Regular Expression),比如由推理规则定义
- (数理逻辑)表达式(Expression)由字、推理规则归纳定义
- 句法(Syntax)
- (数理逻辑)句子(Sentence)由表达式、推理规则归纳定义
- 比如谓词逻辑(Predicate Logic)中的句子
- (编程语言)程序(Program)由单词、推理规则归纳定义
- 比如可计算函数的编程语言PCF中的程序
- 我们通常用上下文无关语法(Context-Free Grammar,CFG)来定义句法,它是和归纳定义、推理规则等价的定义方法。比如,对于从不动点定理到编程语言中的语言
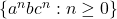 ,其上下文无关语法为(竖线表示“或者”)
,其上下文无关语法为(竖线表示“或者”)
- t = b | atc
- (数理逻辑)句子(Sentence)由表达式、推理规则归纳定义
- 语义(Semantics)
- (数理逻辑)句子的计算称为演算(Calculus)
- 比如Lambda演算中的Beta化归
- (编程语言)程序的计算称为求值(Evaluation)
- 比如求值器(Evaluator)对项求值,解释器(Interpreter)对项、环境求值
- 编译器(Compiler)将程序翻译为机器语言,然后由机器求值。机器求值是由物理定律决定的
- (数理逻辑)句子的计算称为演算(Calculus)
- 自然语言、数学语言、编程语言
- 在算术和算法中,我们同时用自然语言、数学语言、编程语言来描述算法
- 对LLM来说,自然语言(NLP)、数学语言(Math)、编程语言(Code),三者都是语言
一阶逻辑的语言
- 关于命题逻辑,可参见什么是证明?
- 命题逻辑为零阶逻辑,谓词逻辑为一阶逻辑、高阶逻辑。下面我们考虑一阶逻辑
- 一阶逻辑的语言
- 一阶逻辑的公理系统